LCA - Lowest Common Ancestor
A tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree. - Wikipedia
The lowest common ancestor (LCA) is a concept in graph theory and computer science. Let T be a rooted tree with N nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants (where we allow a node to be a descendant of itself). - Wikipedia
Your task in this problem is to find the LCA of any two given nodes v and w in a given tree T.
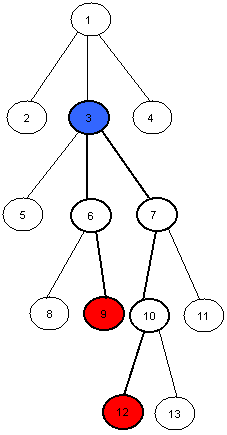
For example the LCA of nodes 9 and 12 in this tree is the node number 3.
Input
The first line of input will be the number of test cases. Each test case will start with a number N the number of nodes in the tree, 1 ≤ N ≤ 1,000. Nodes are numbered from 1 to N. The next N lines each one will start with a number M the number of child nodes of the Nth node, 0 ≤ M ≤ 999 followed by M numbers the child nodes of the Nth node. The next line will be a number Q the number of queries you have to answer for the given tree T, 1 ≤ Q ≤ 1000. The next Q lines each one will have two number v and w in which you have to find the LCA of v and w in T, 1 ≤ v, w ≤ 1,000.
Input will guarantee that there is only one root and no cycles.
Output
For each test case print Q + 1 lines, The first line will have “Case C:” without quotes where C is the case number starting with 1. The next Q lines should be the LCA of the given v and w respectively.
Example
Input: 1 7 3 2 3 4 0 3 5 6 7 0 0 0 0 2 5 7 2 7 Output: Case 1: 3 1
hide comments
|
|
Ayush Mishra:
2015-01-19 05:17:43
Ohh! It turns out that cin is slower than scanf. Scanf on the previous recursive code got accepted, whereas cin gives TLE |
|
|
Ayush Mishra:
2015-01-19 05:17:43
The iterative way to find LCA got me accepted (3.58 s), the similar recurisve function gave TLE! Strange! o.O |
|
|
Tây Cuồng:
2015-01-19 05:17:43
WA because the Query u u, out 0 but the answer is u... hic :(( |
|
|
S:
2015-01-19 05:17:43
test_cases * Q * N solution passed if implemented efficiently :D |
|
|
S:
2015-01-19 05:17:43
I used assert and find that the number of test cases are atleast 100 but no more than 150.
|
|
|
S:
2015-01-19 05:17:43
Although i have solved this question but still i would like to know upper_bound on the number of test cases. |
|
|
Yash Sadhwani:
2015-01-19 05:17:43
take care of tree size........caused me a wa
|
|
|
hamza007:
2015-01-19 05:17:43
Remember to clear the arrays!! Not doing so caused me a lot of TLEs :/ Damn I am stupid ... Last edit: 2014-08-05 09:40:17 |
|
|
kelaseek:
2015-01-19 05:17:43
i think my code's complexity is q*(logn+logn) and 2.26s |
|
|
Tây Cuồng:
2015-01-19 05:17:43
forget to print "CASE C:"... 2WA and AC |
| Added by: | hossamyosef |
| Date: | 2013-05-13 |
| Time limit: | 0.600s-1.113s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | FCIS/ASU Local Contest 2013 |

 RSS
RSS