WARE - The Warehouse
Secret Agent OmeGa-7 has found the secret weapon warehouse of the mad scientist Dr. Matroid. The warehouse is full of large boxes (possibly with deadly weapons inside the boxes). While inspecting the warehouse, OmeGa-7 accidentally triggered the alarm system. The warehouse has a very effective protection against intruders: if the alarm is triggered, then the floor is filled with deadly acid. Therefore, the only way OmeGa-7 can escape is to climb onto the boxes and somehow reach the exit on top of them. The exit is a hole in the ceiling,if OmeGa-7 can climb through this hole then he can escape using the helicopter parked on the roof. There is a ladder and a box below the hole, thus the goal is to reach this box.
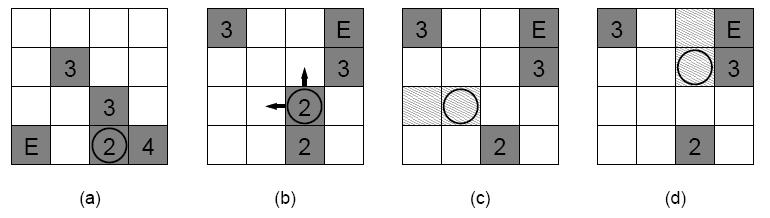
The floor of the warehouse can be divided into a grid containing n * n cells, the size of each cell is 1 meter * 1 meter. Each cell is either fully occupied by one box or unoccupied. Each box is rectangular: the size of the base is 1 meter * 1 meter, and the height is either 2, 3, or 4 meters. In figure (a), you can see an example warehouse, where the numbers show the height of the boxes, E shows the exit, and the circle shows that Secret Agent OmeGa-7 is currently on the top of that box.
OmeGa-7 can do two things:
If he is standing on top of a box, and in an adjacent cell there is another box, then he can move to the top of this other box. For example, in the situation depicted in figure (a), he can move either to north or east, but not to west or south. Note that only these four directions are allowed, diagonal moves are not possible. The height difference between the two boxes does not matter.
The second thing OmeGa-7 can do is that he can topple the box he is standing on in one of the four directions. The effect of toppling is best shown by an example: in the situation shown in figure (b), he can topple the box west (figure (c)) or north (figure (d)). If a box of height h is toppled north (west, south, etc.) then it will occupy h consecutive cells to the north (west, south, etc.) of its original position. The original position will be unoccupied (but can be later occupied again by toppling another box). A box can only be toppled if the cells where it will fall are unoccupied. For example, in figure (a), the box where OmeGa-7 is standing cannot be toppled in any of the four directions.
By toppling a box, OmeGa-7 jumps one step in the direction that the box is toppled (see figures (c) and(d)). If a box is toppled, then it cannot be toppled again later. Recall that there is a box below the exit (at the cell marked with E in the figure), thus it is not possible to topple a box over this cell. The alarm system will soon release mutant poisonous biting bats, so OmeGa-7 has to leave the warehouse as quickly as possible. You have to help him by writing a program that will determine the minimum number of steps required to reach the exit. Moving to an adjacent box, or toppling a box is counted as one step.
Input
The input contains several blocks of test cases. The first line of each block contains three integers: the size 1 <= n <= 8 of the warehouse, and two integers i , j that describe the starting position of the secret agent. These numbers are between 1 and n ; the row number is given by i , the column number is given by j . The next n lines describe the warehouse. Each line contains a string of n characters. Each character corresponds to a cell of the warehouse. If the character is '.', then the cell is unoccupied. The characters '2', '3' and '4' correspond to boxes of height 2, 3 and 4, respectively. Finally, the character 'E' shows the location of the exit.
The input is terminated by a block with n = i = j = 0.
Output
For each test case, you have to output a single line containing an integer: the minimum number of steps required to reach the exit. If it is not possible to reach the exit, then output the text 'Impossible.'(without quotes).
Example
Input: 5 5 3 .2..E ...2. 4.... ....4 ..2.. 0 0 0 Output: 18
hide comments
|
|
Simes:
2020-06-15 07:07:59
That's a very good point @Hodobox, I really must work on my reading and comprehension. Here's an updated example along similar lines. The key being that the 2 height box at r6c3 must first be toppled to the north in order to allow the box at r6c5 to be toppled to the west.
|
|
|
hodobox:
2020-06-13 15:37:31
They definitely don't, as the statement says boxes are of heights 2,3 or 4, never 1. |
|
|
Simes:
2018-06-09 18:39:37
Here are a couple of test cases that you might find useful. I've no idea whether the test data contains cases like these.
|
| Added by: | Fudan University Problem Setters |
| Date: | 2008-07-24 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: C99 ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ACM Central European Programming Contest, Budapest 2005 |

 RSS
RSS