WA - Problems Collection (Volume X)
These ten problems come from Chinese National Olympiad in Mathematics - Province Contest.
Problem 1 Polynomial P(x)=x5+a1x4+a2x3+a3x2+a4x+a5, and we know when k=1, 2, 3, 4, P(k)=2007*k. Calculate P(10)-P(-5).
Problem 2 The sum of 100 positive integers a1, a2, ..., a100 is 2007. Calculate the maximum possible value of 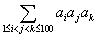 .
.
Problem 3 Calculate 100101102103104......498499500 modulo 126.
Problem 4 We define the sum of the first n numbers of geometric progression {an} Sn. Now we know S7=7, S14=2014. Calculate S7*(S21-S14).
Problem 5 Calculate the sum of this kind of positive integers n(n>=4): n satisfies that n! can be written as the product of n-3 consecutive positive integers.
Problem 6 Two vertices of a square are on the line y=2x-17, while the other two are on the parabola y=x2. Calculate the sum of two different possible values of the area of this square.
Problem 7 A, B, C, D are four fixed points in the space and they are not on the same plane. Calculate the number of different parallelepipeds, which satisfies that 4 vertices of the parallelepiped are A, B, C and D.
Problem 8 Polynomial x2-x-1 exactly divides Polynomial a1x17+a2x16+1. Calculate a1*a2.
Problem 9 Suppose x is an acute angle, calculate the minimum possible value of (sin x +cos x)/(sin x +tan x) + (tan x +cot x)/(cos x +tan x) + (sin x +cos x)/(cos x +cot x) + (tan x +cot x)/(sin x +cot x).
Problem 10 Suppose x4+y4+z4=m/n, x, y, z are all real numbers, satisfying x*y+y*z+z*x=1 and 5*(x+1/x)=12*(y+1/y)=13*(z+1/z); m, n are positive integers and their greatest common divisor is 1. Calculate m+n.
Input
There is no input.
Output
Ten lines, each contains a single integer denoted the answer to the correspoding problem.
Example
There is no example.
| Added by: | Fudan University Problem Setters |
| Date: | 2007-09-27 |
| Time limit: | 0.100s |
| Source limit: | 60B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | TEXT |
| Resource: | CMOP :) |

 RSS
RSS