TILE001 - Black and White Tiles
Cradi and Vank are very fond of tiles. They have rectangular tiles of breadth 1 cm (black or white) and 2 cm (only black), with any possible length greater than zero in infinite supply.
They try to make different arrangements using the tiles available to them. Two arrangements are considered same if (with or without rotation) all the tiles sizes and colors overlap with no mismatch.
They initially have a square tile of dimension (1 cm X 1 cm) of grey color which they call 0-layer arrangement. They can add new layers of tiles keeping in mind the following constraints:
After completing any i layer arrangement:
1) Use 2 black and 2 white tiles of breadth 1 cm with length 2i + 1 and 2i + 3 to get an (i + 1)-layer arrangement.
2) Use 4 black tiles of breadth 2 cm with length 2i + 1 or 2i + 5 to get an (i + 2)-layer arrangement.
All this is done keeping in mind that adjacent tiles of same layer cannot have same color, unless they are all of 2 cm breadth (then they are all black). Some possible 2 layer arrangements are shown in the figure.
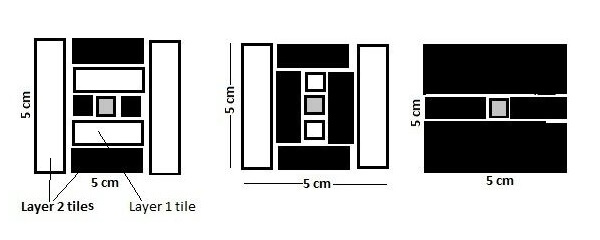
In their desire to explore different arrangements they stumble across this strange question as to how many different n-layer arrangements are possible for any given n. Your job is to find the answer to this query. Since the answer can be very large, print the answer modulo (10^9 + 7).
Input
First line contains T i.e. the number of test cases. Then T line follow each containing n.
Output
Print the answer for each n.
Example
Input: 3 0 1 2 Output: 1 2 9
Constraints
t <= 1000
0 <= n <= 1000000
hide comments
|
|
Francky:
2015-01-31 18:47:33
>2) Use 4 black tiles of breadth 2 cm with length 2i + 1 and 2i + 5 to get an (i + 2)-layer arrangement.
|
| Added by: | Aniket Kumar |
| Date: | 2015-01-21 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 JS-MONKEY |
| Resource: | Own |

 RSS
RSS