PROG0598 - Baseball
Baseball is a bat-and-ball game played between two teams of nine players. The sport is very popular in North America and parts of Central and South America, the Caribbean, and East Asia, but less popular in Europe. The teams switch between batting and fielding whenever the fielding team records three outs. One turn batting for both teams, beginning with the visiting team, constitutes an inning. A game comprises nine innings, and the team with the greater number of runs at the end of the game wins. Baseball is the only major team sport in America with no game clock, although almost all games end in the ninth inning.
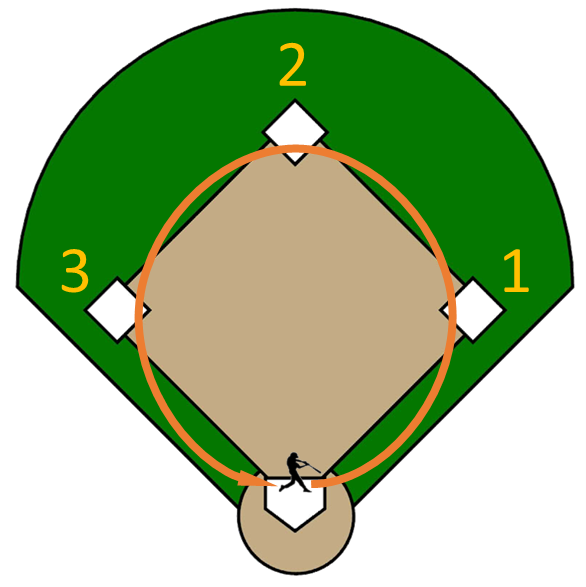
The batting team attempts to score runs by hitting a ball that is thrown by the pitcher with a bat swung by the batter, then running counter-clockwise around a series of four bases (indicated by the white squares in the figure below): first, second, third, and home plate (bottom white square in the figure). A run is scored when a player advances around the bases and returns to home plate. Players on the batting team take turns hitting against the pitcher of the fielding team, which tries to prevent runs by getting hitters out in any of several ways. A player of the batting team who reaches a base safely can later attempt to advance to subsequent bases during teammates' turns batting, such as on a hit or by other means. A home run is scored when the ball is hit in such a way that the batter is able to circle the bases and reach home safely in one play without any errors being committed by the defensive team in the process.
In this assignment we only consider $\mathbf{n}$-base hits, where $n \in \mathbb{N}$ and $0 \leq n \leq 4$. With a $0$-base hit the batter could not hit the ball correctly, and is not allowed to enter the field (so that he can not score a point). With an $n$-base hit ($0 < n \leq 4$) all players of the batting team on the field (the batter and the players occupying bases) advance $n$ bases counter-clockwise around the field. All players that return to home plate upon this hit score a point and leave the field. A home run is therefore equal to a 4-base hit.
Assignment
During a baseball game, only the first, second and third base may be occupied. We will therefore represent the occupied bases during game play by a list or a tuple that may only contain the integers 1 (first base), 2 (second base) and 3 (third base). The integers are always arranged in increasing order.
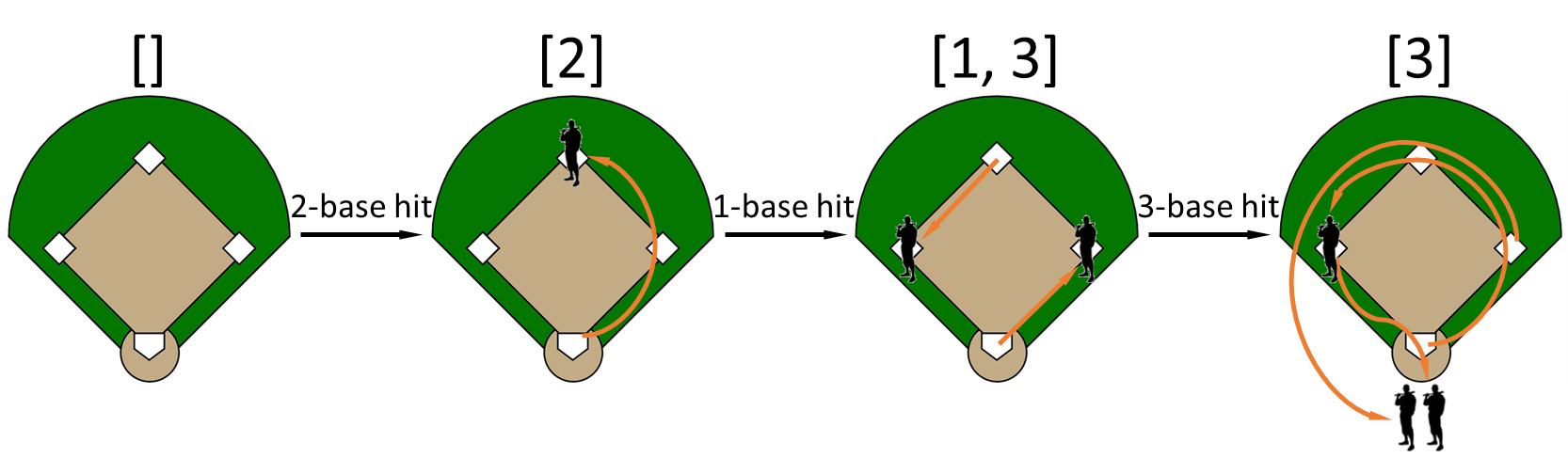
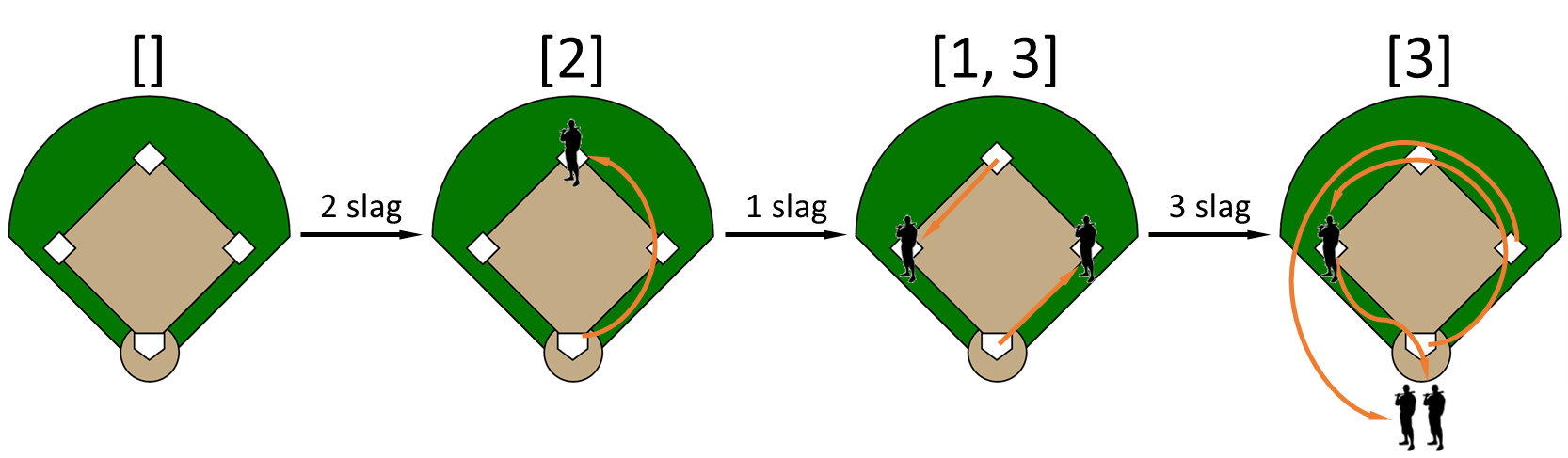
There are no occupied bases at the start of a batting turn, which is represented by an empty list (situation on the left in the above figure). In case the first batter strikes a 2-base hit, he runs over first base to second base. If the second batter then strikes a 1-base hit, he runs to first base and the first batter advances to third base. If the third batter then strikes a 3-base hit, he runs to third base and the first two batters that occupied first and third base each score one point because they reach the home plate. Your task:
- Write a function hit that takes an integer $n \in \mathbb{N}$ ($0 \leq n \leq 4$) as its argument. The function also has a second optional parameter occupied that may take a list or a tuple of integers, representing the bases that were occupied before the batter entered the field. The function must return a tuple containing two values that describe the situation of the game after the batter has stroke an $n$-base hit: i) the points scored (an int) by all players of the batting team during that hit and ii) all bases that are occupied after the hit (a list).
- Write a function inning that takes a list or a tuple of integers in the range [0, 4]. These integers represent the successive $n$-base hits of a team during one batting turn. The function must return a tuple containing two values: i) the points scored (an int) by the batting team during that batting turn and ii) the bases that are occupied at the end of the batting turn (a list).
Example
>>> hit(2) (0, [2]) >>> hit(0, [1, 3]) (0, [1, 3]) >>> hit(1, (1, 3)) (1, [1, 2]) >>> hit(2, occupied=[1, 3]) (1, [2, 3]) >>> hit(3, occupied=(1, 3)) (2, [3]) >>> hit(4, occupied=[1, 3]) (3, []) >>> inning([0, 1, 2, 3, 4]) (4, []) >>> inning((4, 3, 2, 1, 0)) (2, [1, 3]) >>> inning([1, 1, 2, 1, 0, 0, 1, 3, 0]) (5, [3])
Honkbal is een balsport waarin twee teams van negen spelers het tegen elkaar opnemen. De sport is vooral populair in de Verenigde Staten, Canada, Mexico, de Caraïben en grote delen van Azië. In Europa is de sport minder populair. Een wedstrijd bestaat uit negen innings, en elke inning bestaat uit twee speelhelften. In de ene speelhelft verdedigt het thuisspelende team in het veld en is het bezoekende team in de aanval. In de andere speelhelft zijn de rollen omgedraaid. Alleen het aanvallende team kan punten scoren.
Het speelveld bestaat uit vier honken in de vorm van een ruit, aangegeven door de witte vlakken in onderstaande figuur. Op de thuisplaat (witte vlak onderaan) is telkens een volgende speler van het aanvallende team aan slag. Deze speler wordt de slagman genoemd. Een werper van het verdedigende team gooit een bal naar de thuisplaat waar de slagman van het aanvallende team hem moet proberen te raken. Als de slagman de bal kan raken, dan moet hij in tegenwijzerzin één voor één de honken proberen te bereiken voor het verdedigende team de bal bij het honk kan brengen. Indien er bij de slag reeds honken bezet waren door andere aanvallende spelers, dan mogen deze ook proberen om de volgende honken te bereiken (in tegenwijzerzin). Wanneer een aanvallende speler alle vier de honken is gepasseerd, dan scoort hij één punt. Wanneer een slagman alle honken in zijn eigen slagbeurt kan passeren, dan heet dat een homerun.
In deze opgave houden we enkel rekening met $\mathbf{n}$-slagen, waarbij $n \in \mathbb{N}$ en $0 \leq n \leq 4$. Bij een 0-slag kan de slagman de bal niet raken, en mag hij het veld niet betreden (waardoor hij ook geen punten kan scoren). Bij een $n$-slag ($0 < n \leq 4$) lopen alle aanvallende spelers op het veld (de slagman en alle spelers die reeds honken bezet hielden) $n$ honken vooruit in tegenwijzerzin. Alle spelers die hierbij de thuisplaat bereiken, scoren een punt en stappen uit het veld. Een homerun is dus gelijk aan een 4-slag.
Opgave
Bij het spelletje honkbal kunnen enkel het eerste, tweede en derde honk bezet worden door aanvallende spelers. Daarom stellen we in deze opgave de bezette honken voor als een lijst die of een tuple dat enkel de getallen 1 (eerste honk), 2 (tweede honk), en 3 (derde honk) kan bevatten. De getallen worden altijd in stijgende volgorde opgelijst.
Bij aanvang van een speelhelft zijn er nog geen honken bezet, wat kan worden voorgesteld door een lege lijst (linkse situatie in bovenstaande figuur). Indien de eerste slagman een 2-slag laat optekenen, dan loopt hij over het eerste honk naar het tweede honk. Indien de tweede slagman daarna een 1-slag doet, dan loopt hij naar het eerste honk en loopt de eerste slagman door naar het derde honk. Indien de derde slagman daarna een 3-slag doet, dan loopt hij naar het derde honk en scoren de twee aanvallende spelers die reeds het eerste en derde honk bezet hielden elk één punt omdat ze de thuisplaat bereiken. Gevraagd wordt:
- Schrijf een functie slag waaraan een getal $n \in \mathbb{N}$ ($0 \leq n \leq 4$) moet doorgegeven worden. De functie heeft ook nog een tweede optionele parameter bezet waaraan een lijst of een tuple kan doorgegeven worden, die aangeeft welke honken bezet waren voor de slagman op het veld kwam. Indien er geen expliciete waarde wordt doorgegeven aan de parameter bezet, dan zijn er nog geen honken bezet. De functie moet een tuple teruggeven met twee waarden die de spelsituatie beschrijven nadat de slagman een $n$-slag gedaan heeft: i) de punten (een int) die door alle aanvallende spelers behaald werden bij die slag en ii) de honken die bezet zijn na de slag (een lijst).
- Schrijf een functie inning waaraan een lijst of een tuple van natuurlijke getallen uit het interval [0, 4] moet doorgegeven worden. Deze getallen stellen de opeenvolgende $n$-slagen voor die binnen één speelhelft gedaan werden. De functie moet een tuple met twee waarden teruggeven: i) de punten (een int) die het aanvallende team behaald heeft tijdens de speelhelft en ii) de honken die bezet zijn op het einde van de speelhelft (een lijst).
Voorbeeld
>>> slag(2) (0, [2]) >>> slag(0, [1, 3]) (0, [1, 3]) >>> slag(1, (1, 3)) (1, [1, 2]) >>> slag(2, bezet=[1, 3]) (1, [2, 3]) >>> slag(3, bezet=(1, 3)) (2, [3]) >>> slag(4, bezet=[1, 3]) (3, []) >>> inning([0, 1, 2, 3, 4]) (4, []) >>> inning((4, 3, 2, 1, 0)) (2, [1, 3]) >>> inning([1, 1, 2, 1, 0, 0, 1, 3, 0]) (5, [3])
| Added by: | Peter Dawyndt |
| Date: | 2015-12-01 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |

 RSS
RSS