SPOJ.com - Problem PROG0578

PROG0578 - Transitions and transversions

no tags

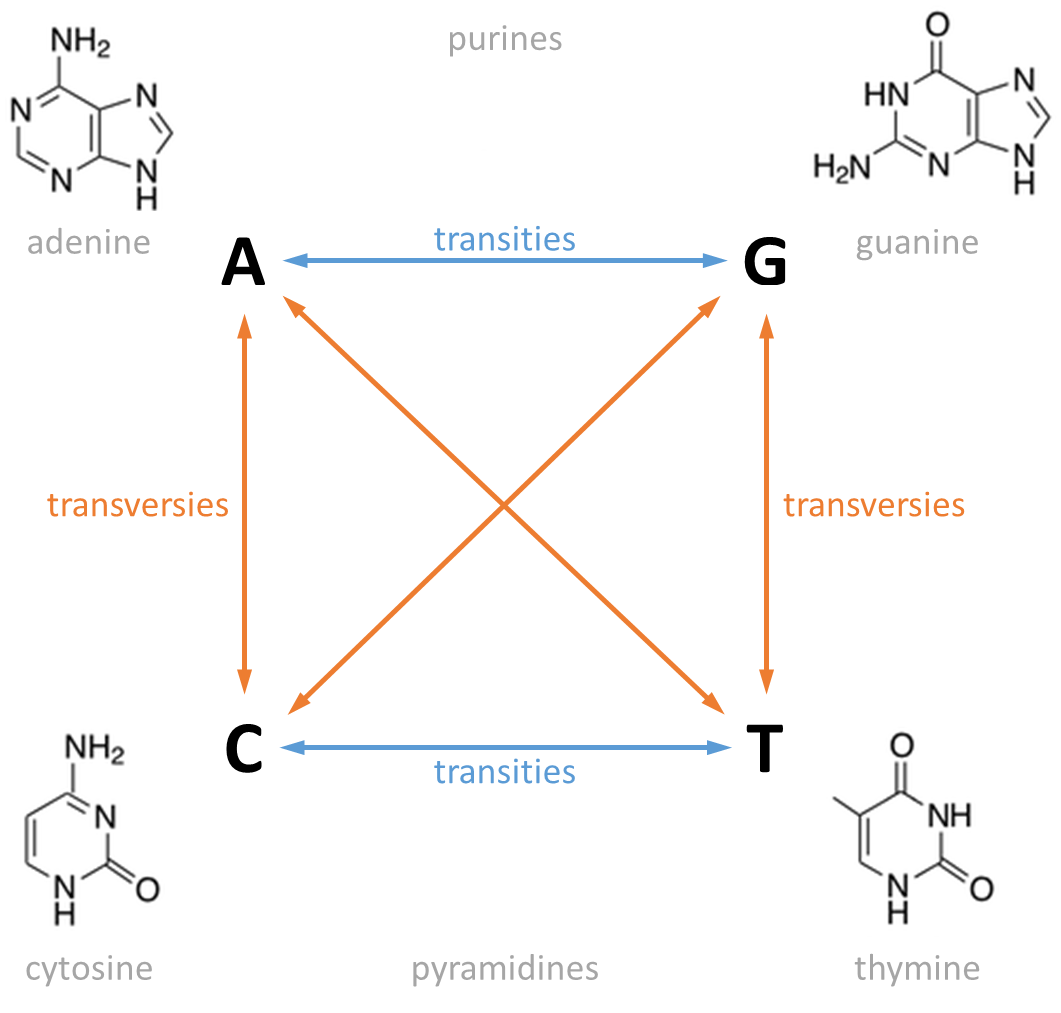
In genetics, a distinction is made between two types of mutations (the replacement of one nucleotide by a different nucleotide). A transition changes a purine nucleotide (two rings) into another purine (A ↔ G), or changes a pyrimidine nucleotide (one ring) into another pyrimidine (C ↔ T). All other mutations in which a purine is substituted for a pyrimidine, or vice versa, are called transversions.

Although in theory there are only four possible transitions and eight possible transversions, in practice transitions are more likely than transversions because substituting a single ring structure for another single ring structure is more likely than substituting a double ring for a single ring. Also, transitions are less likely to result in amino acid substitutions (due to wobble base pair) and are therefore more likely to persist as silent substitutions in populations.

Assignment

In this assignment we represent DNA sequences as strings that only contains the letters A, C, G and T. These letters represent the nucleotides that make up the DNA sequence. The nucleotides can also be represented using their lowercase variants. Given two DNA sequences $s_1$ and $s_2$ that have the same length, we define their transition/transversion ratio $R(s_1, s_2)$ as the ratio of the number of transitions to the number of transversions, where nucleotides at the corresponding positions between the two DNA sequences are compared with each other.

The transition/transversion ratio between homologous strands of DNA is generally about 2, but it is typically elevated in coding regions, where transversions are more likely to change the underlying amino acid and thus possibly lead to a fatal mutation in the translated protein. Point mutations that do not change this amino acid (which are thus more likely for transitions) are called silent substitutions. Your task:

Write a function transition that takes two nucleotides as its arguments. The function must return a Boolean value that indicates whether or not replacing the first nucleotide by the second nucleotide leads to a transition.
Write a function transversion that takes two nucleotides as its arguments. The function must return a Boolean value that indicates whether or not replacing the first nucleotide by the second nucleotide leads to a transversion.
Write a function ratio that takes two DNA sequences $s_1$ and $s_2$ as its arguments. The function may assume that both sequences have the same length (the function does not need to check this explicitly). The function must return the transition/transversion ratio $R(s_1, s_2) \in \mathbb{R}$ of the two given sequences as a floating point number. In case there are no transversions between the two sequences, $R(s_1, s_2) = 0$ by definition.

None of these function may make a distinction between uppercase and lowercase letters in the arguments passed to the functions.

Example

>>> transition('G', 'A')
True
>>> transition('t', 'g')
False
>>> transition('C', 'c')
False

>>> transversion('G', 'A')
False
>>> transversion('t', 'g')
True
>>> transversion('C', 'c')
False

>>> ratio('ATTAGCATTATCATC', 'AAATAGGATATATGG')
0.2222222222222222

>>> seq1 = 'GCAACGCACAACGAAAACCCTTAGGGACTGGATTATTTCGTGATCGTTGTAGTTATTGGAAGTACGGGCATCAACCCAGTT'
>>> seq2 = 'ttatctgacaaagaaagccgtcaacggctggataatttcgcgatcgtgctggttactggcggtacgagtgttcctttgggt'
>>> ratio(seq1, seq2)
1.2142857142857142

In de genetica wordt onderscheid gemaakt tussen twee soorten mutaties (de vervanging van één nucleotide door een andere nucleotide). Bij transities wordt een purine nucleotide (twee ringen) vervangen door een andere purine (A ↔ G), of wordt een pyramidine nucleotide (één ring) vervangen door een andere pyramidine (C ↔ T). Alle andere mutaties waarbij een pyrine wordt vervangen door een pyramidine, of vice versa, worden transversies genoemd.

Ondanks het feit dat er in theorie slechts vier transities en acht transversies mogelijk zijn, is de kans op een transitie in de praktijk veel groter dan die van een transversie omdat het vervangen van een enkele ringstructuur door een andere enkele ringstructuur veel waarschijnlijker is dan het vervangen van een dubbele ring door een enkele ring. Bovendien leiden transities ook minder snel tot een aminozuursubstitutie, waardoor ze ook vaker overleven als stille substituties binnen een populatie.

Opgave

In deze opgave stellen we DNA sequenties voor als strings die enkel bestaat uit de letters A, C, G en T, die de verschillende nucleotiden voorstellen. De nucleotiden mogen ook met kleine letters geschreven worden. Gegeven twee even lange DNA sequenties $s_1$ en $s_2$, dan definiëren we de transitie/transversieverhouding $R(s_1, s_2)$ als de verhouding van het aantal transities ten opzicht van het aantal transversies, waarbij telkens de nucleotiden op overeenkomstige posities tussen de twee sequenties met elkaar vergeleken worden.

De transitie/transversieverhouding tussen twee homologe DNA sequenties ligt meestal rond de 2, maar is typisch een stuk hoger binnen eiwitcoderende gebieden omdat transversies daar doorgaans de aminozuursamenstelling wijzigen en dus mogelijk aanleiding geven tot fatale mutaties in het vertaalde eiwit. Puntmutaties die geen aanleiding geven tot een wijziging in het aminozuur (wat een stuk waarschijnlijker is voor transities) worden stille substituties genoemd. Gevraagd wordt:

Schrijf een functie transitie waaraan twee nucleotiden moeten doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de vervanging van de ene nucleotide door de andere al dan niet een transitie voorstelt.
Schrijf een functie transversie waaraan twee nucleotiden moeten doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de vervanging van de ene nucleotide door de andere al dan niet een transversie voorstelt.
Schrijf een functie verhouding waaraan twee DNA sequenties $s_1$ en $s_2$ moeten doorgegeven worden. De functie mag ervan uitgaan dat deze twee DNA sequenties even lang zijn (en moet dit niet expliciet controleren). De functie moet de transitie/transversieverhouding $R(s_1, s_2) \in \mathbb{R}$ van de twee gegeven sequenties teruggeven als een floating point getal. Hierbij geldt dat $R(s_1, s_2) = 0$ als er geen transversies zijn tussen de twee gegeven sequenties.

Geen enkele van deze drie functies mag onderscheid maken tussen hoofdletters en kleine letters in de argumenten die aan de functies doorgegeven worden.

Voorbeeld

>>> transitie('G', 'A')
True
>>> transitie('t', 'g')
False
>>> transitie('C', 'c')
False

>>> transversie('G', 'A')
False
>>> transversie('t', 'g')
True
>>> transversie('C', 'c')
False

>>> verhouding('ATTAGCATTATCATC', 'AAATAGGATATATGG')
0.2222222222222222

>>> seq1 = 'GCAACGCACAACGAAAACCCTTAGGGACTGGATTATTTCGTGATCGTTGTAGTTATTGGAAGTACGGGCATCAACCCAGTT'
>>> seq2 = 'ttatctgacaaagaaagccgtcaacggctggataatttcgcgatcgtgctggttactggcggtacgagtgttcctttgggt'
>>> verhouding(seq1, seq2)
1.2142857142857142

Submit solution!

Added by:	Peter Dawyndt
Date:	2015-10-15
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC