PROG0567 - Nob number puzzle
This assignment is a tribute to the late Japanese puzzle maven Nobuyuki Yoshigahara (芦ヶ原 伸之 ,1936–2004). This brilliant guru, inventor, collector and solver of puzzles — commonly known in Japan as Nob — graduated from the Tokyo Institute of Technology in applied chemistry. After becoming disenchanted with his research career in high-polymer engineering, Nob turned to high school teaching as an educator of chemistry and mathematics.
It is very difficult to give a simple and brief illustration to Nob's puzzle work since his ingenuity and diapason of his interests and achievements was quite incomparable. Numbers were a big passion of Nob, and his ingenuity in this field was amusing. In every number he could find some interesting rule or property. The following conundrum Nob considered as his masterpiece.
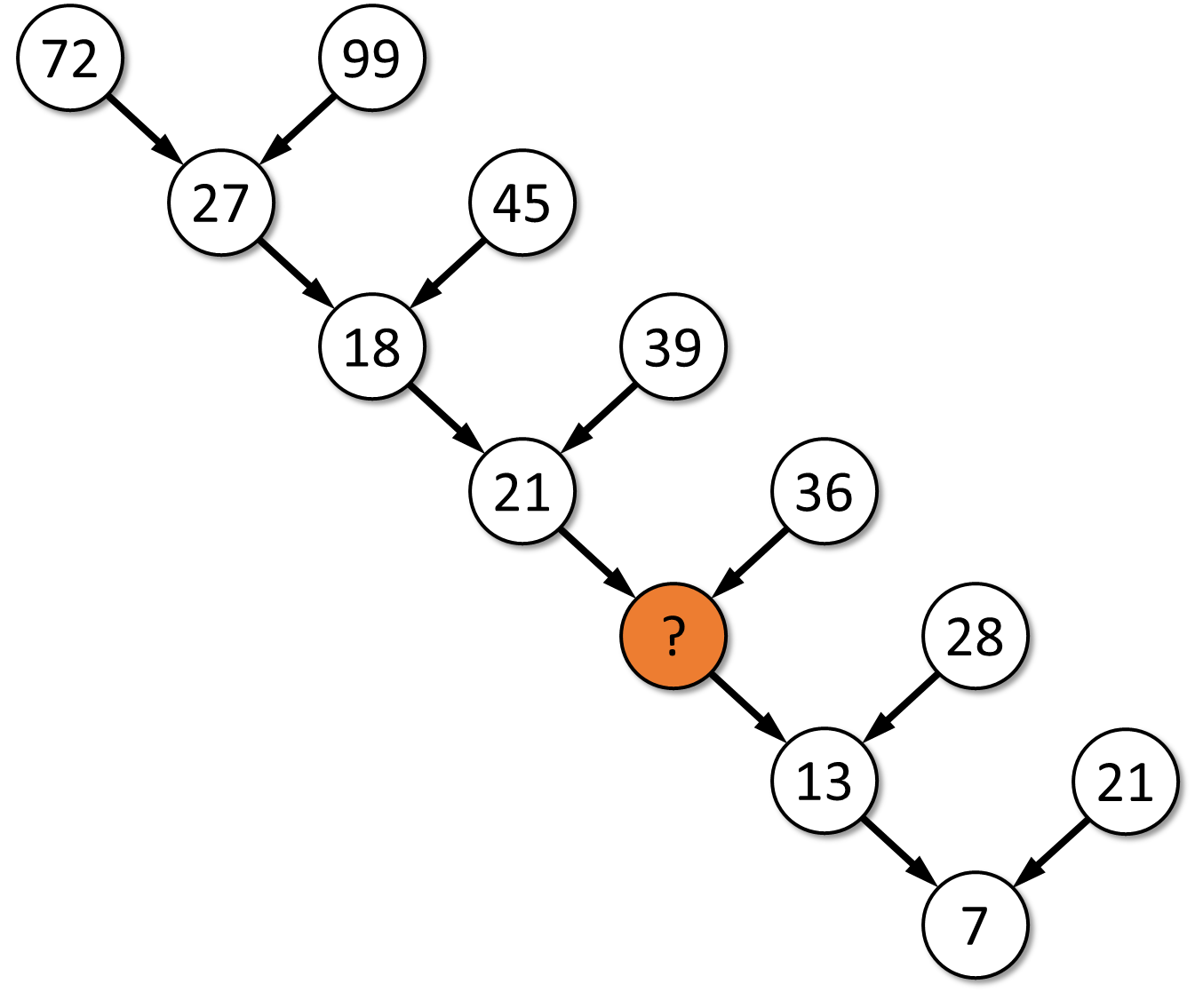
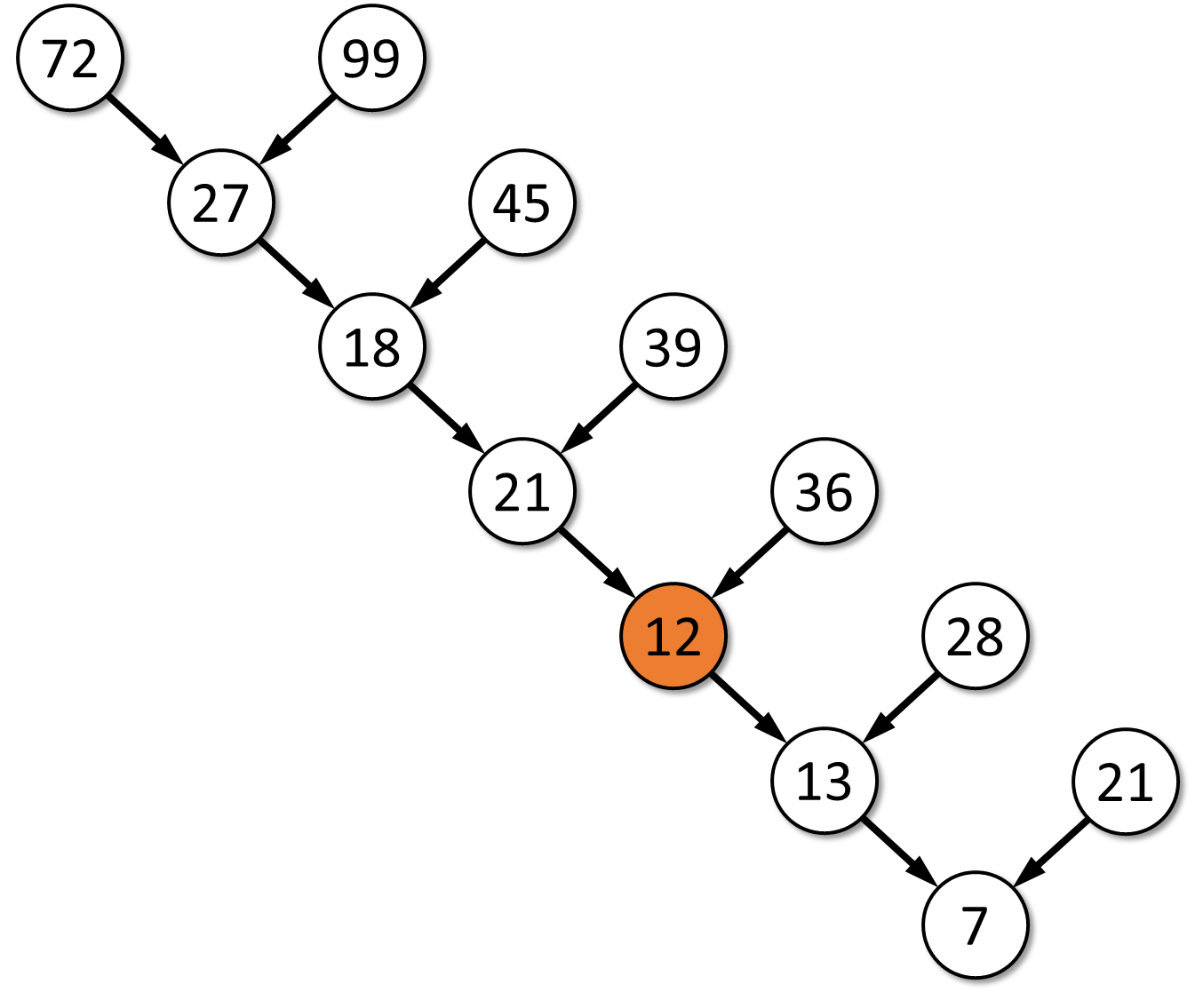
This puzzle is brilliant in it's simplicity: the numbers that have been filled into the tree above are put in the nodes according to a certain rule; according to this rules, which number should be put instead of the question mark? Lee Sallows writes, "You have to solve this yourself, otherwise you won't see how beautiful it is.". Don't think you have found the correct answer if the rule you came up with seems to suggest that there must be a typo in the puzzle. All numbers in the tree have been double checked and are correct. Click here to see the answer.
Input
The input contains a sequence of positive integers, each on a separate line. The sequence contains at least one integers and ends with the integer -1, which is not part of the actual sequence.
Output
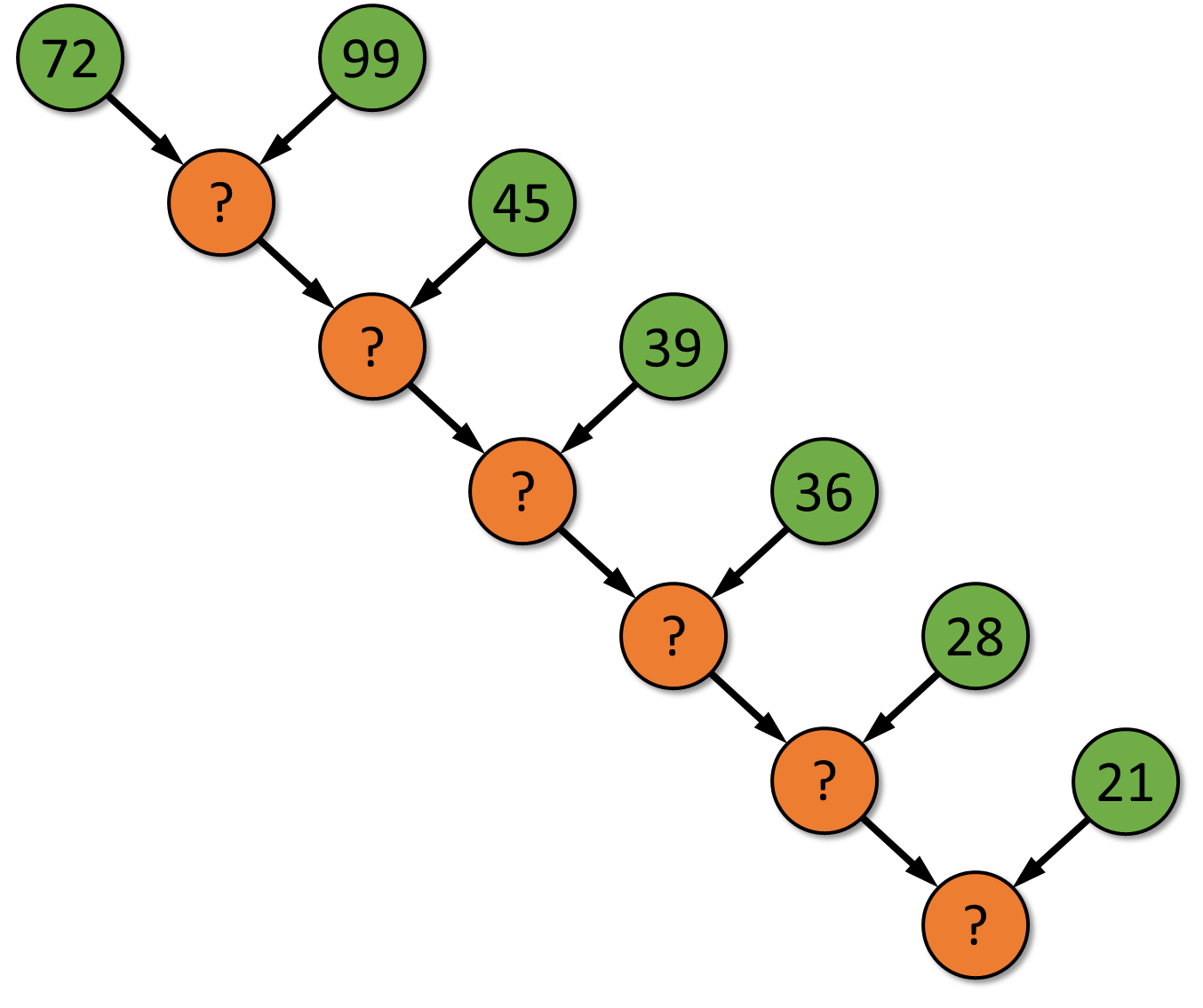
The given sequence of integers are the top numbers in a tree, like the one used in the Nob's number puzzle. For the example at the bottom of this assignment, the given sequence of numbers is used to fill the nodes indicates in green in the figure below.
Your task is to complete the tree by filling up the missing numbers in the orange colored nodes. These missing numbers can be computed as the sum of the digits of the two numbers in the nodes above the orange nodes.
The output needs to be formatted in the following way. Each line contains two integers from the tree. The first line has no indentation, and each successive line has two additional spaces of indentation with respect to the previous line. The two numbers follow the indentation, with each number centered over four positions. None of the output lines may have spaces at the end of the line.
Example
Input:
72 99 45 39 36 28 21 -1
Output:
72 99
27 45
18 39
21 36
12 28
13 21
7
Deze opgave is een eerbetoon aan de grootste Japanse guru, bedenker en verzamelaar van raadsels Nobuyuki Yoshigahara (芦ヶ原 伸之 ,1936–2004). Dit genie in het oplossen van puzzels — die bij iedereen in Japan bekend staat onder de naam Nob — behaalde een diploma in de toegepaste chemie aan het Tokyo Institute of Technology. Na een korte en ietwat ontgoochelende onderzoekscarrière in de polymeerchemie, stortte hij zich volledig op het lesgeven van chemie en wiskunde in het middelbaar onderwijs.
Het hele oeuvre van grootmeester Nob laat zich ontzettend moeilijk in een notendop vatten, omdat de veelzijdigheid van zijn verwezenlijken en zijn vindingrijkheid nauwelijks hun gelijke kennen. Nob had een grote passie voor getallen, en de volgende vernuftige puzzel wordt algemeen beschouwd als één van zijn meesterwerken.
Deze puzzel is briljant in zijn eenvoud: welk getal ontbreekt op de plaats van het vraagteken? Of zoals Lee Sallows het omschrijft: "Je moet deze puzzel zelf oplossen, anders zal je er nooit de schoonheid van inzien.". Denk vooral maar niet te snel dat je het antwoord gevonden hebt en dat er een typfout in de opgave geslopen is. De reeds ingevulde getallen zijn wel degelijk correct. Klik hier om het antwoord zichtbaar te maken.
Invoer
De invoer bestaat uit een reeks natuurlijke getallen, elk op een afzonderlijke regel. Deze reeks bevat minstens één getal en wordt afgesloten door het getal -1, dat zelf geen deel uitmaakt van de reeks.
Uitvoer
De gegeven getallen vormen de bovenste getallen uit een boom zoals die gebruikt wordt in het bovenstaande raadsel van Nob Yoshigahara. Voor onderstaand voorbeeld staat de reeks getallen uit de invoer hieronder ingekleurd in het groen.
Je opdracht bestaat erin om de boom verder aan te vullen door de getallen te berekenen die op de oranje posities moeten ingevuld worden. Deze getallen kan je vinden door telkens de som van de cijfers te bepalen van de twee getallen die erboven staan.
De uitvoer moet op de volgende manier opgemaakt worden. Op elke regel staan er twee getallen uit de boom. Op de eerste regel is er geen insprong, en elke volgende regel begint met een insprong die telkens twee spaties groter is dan de insprong op de vorige regel. Daarna moeten de twee getallen uitgeschreven worden, waarbij elk getal gecentreerd wordt over vier posities. Aan het einde van een regel mogen er geen spaties staan.
Voorbeeld
Invoer:
72 99 45 39 36 28 21 -1
Uitvoer:
72 99
27 45
18 39
21 36
12 28
13 21
7
| Added by: | Peter Dawyndt |
| Date: | 2015-10-04 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |


 RSS
RSS