PROG0537 - Spectroscopy
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted due to an atom or molecule making a transition from a high energy state to a lower energy state. The energy of the emitted photon is equal to the energy difference between the two states. There are many possible electron transitions for each atom, and each transition has a specific energy difference. This collection of different transitions — leading to different radiated wavelengths — make up an emission spectrum. Each element's emission spectrum is unique. As an example, the following image shows the visible hydrogen emission spectrum that contains four main spectral lines.
As a result, spectroscopy can be used to identify the elements in matter of unknown composition. Similarly, the emission spectra of molecules can be used in chemical analysis of substances. This requires taking into account a number of different forms of variation that may occur when determining emission spectra. Because of measurement errors, measured wavelengths of spectral lines usually deviate slightly from the corresponding spectral lines in an emission spectrum used as a reference. In addition, it is not necessarily the case that all possible electron transitions take place in the substance under investigation, so that the corresponding spectral lines are not measured. Due to interference between the different atoms in a substance, additional spectral lines might also appear that do not occur in the reference spectra of the individual atoms.
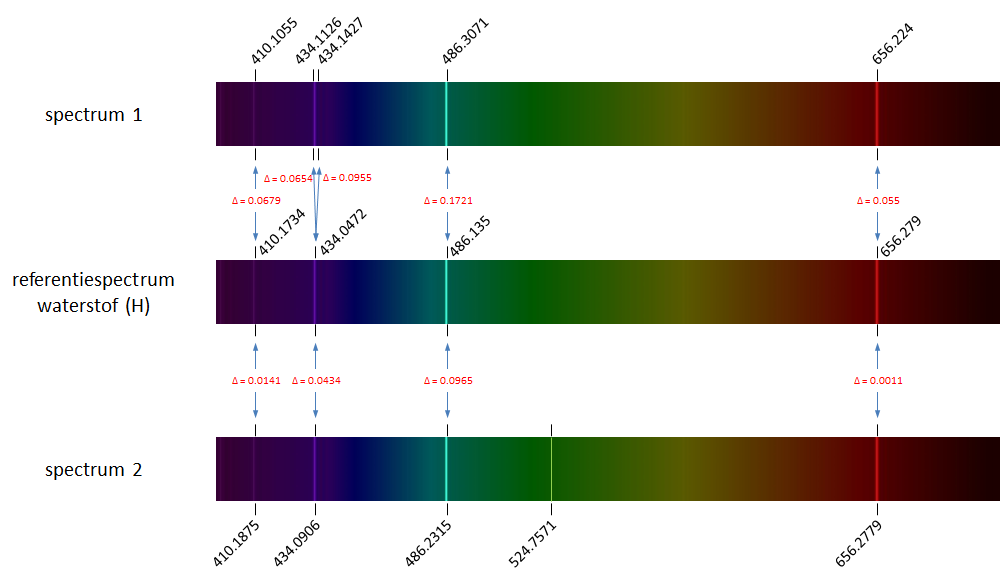
The figure above shows the reference spectrum of hydrogen (middle) containing four spectral lines. The spectra on top and below the reference spectrum are emission spectra of hydrogen as measured in the lab. We observe slight deviations in the measured wavelengths of the spectral lines (wavelengths are indicated above or below the spectra). All corresponding spectral lines between the reference spectrum and the measured spectra are indicates by blue arrows, which also contain the abolsute value of the deviation ($\Delta$). The spectrum on top shows a duplication of the second spectral line from the reference spectrum caused by a measurement error. The spectrum at the bottom shows a spurious spectral line popping up at wavelength 524.8 nm.
Assignment
In this exercise we will represent the emission spectrum of an atom or a chemical substance as a tuple of floating point numbers. These numbers represent the wavelengths of the spectral lines in the emission spectrum, and are always in increasing order.
If we store the reference spectra of a series of atoms in a text file, we use a format that has the symbolic name of each atom on a separate line, followed by a tab and the wavelengths of the spectral lines in the emission spectrum of that atom. The wavelengths of the spectral lines are separated from each other using commas (,). In this storage format, the wavelengths are not necessarily in increasing order. The following example shows the content of the file spectra.txt.
H 486.135,434.0472,656.279,410.1734 He 501.56783,667.8151,587.5621,471.31457,492.19313,504.7738,447.14802,438.79296,402.61914,412.08154 Li 610.354,670.791,413.259,610.365,670.776 Hg 404.6565,407.7837,434.74945,435.8335,535.4034,546.075,567.581,576.961,579.067,580.3782,585.9254,671.634,690.746
Your task:
- Write a function referenceSpectra that takes the location of a text file. This text file must contain the reference spectra of a series of atoms. The function must return a dictionary that maps the symbolic name of each atom in the file onto its reference spectrum. A reference spectrum is represented as a tuple containig the wavelengths of the spectral lines in the reference spectrum, represented as floating point numbers and sorted in increasing order.
- Write a function referenceLines that takes two emission spectra. The first spectrum represents a measured spectrum and the second spectrum a reference spectrum. The function also has a third optional parameter eps that takes a floating point value $\epsilon$ (default value 0.1). The value $\epsilon$ represents the maximal deviation allowed between corresponding spectral lines in the two given spectra. The function must return a positive integer that indicates the number of spectral lines in the reference spectrum that have at least one corresponding spectral line in the measured spectrum. A spectral line having wavelength $g_r$ in the reference spectrum corresponds to a spectral line having wavelength $g_m$ in the measured spectrum if $|g_r - g_m| \leq \epsilon$.
- Write a function decomposition that takes two arguments: a measured spectrum and a dictionary of reference spectra. The dictionary must be formatted as the dictionaries returned by the function referenceSpectra. The function also has an optional parameter eps that has the same meaning and default value as with the function referenceLines. The function also has an optional parameter minimum that may take a positive integer. The function must return an alphabetically sorted list of the symbolic names of all atoms that occur in the given dictionary, whose corresponding reference spectrum has a "sufficient" number of corresponding spectral lines in the measured spectrum. The function referenceLines must be used to determine the number of corresponding spectral lines between the measured spectrum and a reference spectrum, as well as the value passed to the parameter eps. In case a value was explicitly passed to the parameter minimum, this value indicates the minimum number of corresponding spectral lines that is considered to be "sufficient". In case no explicit value was passed to the parameter minimum, the number of corresponding spectral lines is only "sufficient" is all spectral lines in the reference spectrum have a corresponding spectral line in the measured spectrum.
Example
In the following interactive session, we assume that the text file spectra.txt is located in the current directory.
>>> referenceSpectrum = referenceSpectra('spectra.txt') >>> referenceSpectrum['H'] (410.1734, 434.0472, 486.135, 656.279) >>> referenceSpectrum['Li'] (413.259, 610.354, 610.365, 670.776, 670.791) >>> referenceSpectrum >>> spectrum1 = (410.1055, 434.1126, 434.1427, 486.3071, 656.224) >>> referenceLines(spectrum1, referenceSpectrum['H']) 3 >>> spectrum2 = (410.1875, 434.0906, 486.2315, 524.7571, 656.2779) >>> referenceLines(spectrum2, referenceSpectrum['H'], eps=0.1) 4 >>> referenceLines(spectrum2, referenceSpectrum['H'], eps=0.025) 2 >>> spectrum = (402.5579, 410.1914, 413.162, 434.1243, 486.0598, 504.7387, 610.157, 610.562, 656.354, 670.578, 670.991) >>> decomposition(spectrum, referenceSpectrum) ['H'] >>> decomposition(spectrum, referenceSpectrum, eps=0.2) ['H', 'Li'] >>> decomposition(spectrum, referenceSpectrum, minimum=2) ['H', 'He'] >>> decomposition(spectrum, referenceSpectrum, eps=0.2, minimum=2) ['H', 'He', 'Li']
Het emissiespectrum van een chemisch element of chemische verbinding is het frequentiespectrum van de electromagnetische straling die wordt uitgezonden wanneer een atoom of een molecule overgaat van een hoge energietoestand naar een lage energietoestand. De energie van het uitgezonden foton is gelijk aan het verschil in energie tussen de twee toestanden. Elk atoom heeft verschillende mogelijke elektronentransities, die elk corresponderen met een specifiek energieverschil. Deze verzameling van mogelijke transities — die aanleiding geven tot een straling in verschillende golflengten — vormt een emissiespectrum. Elk chemisch element heeft een uniek emissiespectrum. Bij wijze van voorbeeld tonen we hieronder het referentiespectrum van waterstof (H) waarop vier spectraallijnen te zien zijn.
Spectroscopie kan dus gebruikt worden om de atomen te identificeren die voorkomen in een stof met onbekende samenstelling. De emissiespectra van moleculen kunnen ook gebruikt worden bij de chemische analyse van stoffen. Hierbij moet rekening gehouden worden met een aantal vormen van variatie die kunnen optreden bij het bepalen van emissiespectra. Door meetfouten wijkt de gemeten golflengte van een spectraallijn doorgaans lichtjes af van een spectraallijn in een emissiespectrum dat als referentie gebruikt wordt. Bovendien vinden bij het bepalen van het energiespectrum van een bepaalde stof niet noodzakelijk alle mogelijke elektronentransities plaats, waardoor de corresponderende spectraallijnen niet gemeten worden. Door interferenties tussen atomen kunnen er ook spectraallijnen opduiken die niet in de referentiespectra van de individuele atomen voorkomen.
Hierboven tonen we opnieuw het referentiespectrum van waterstof (midden) waarop vier spectraallijnen te zien zijn. Bovenaan en onderaan de figuur staan twee emissiespectra van waterstof zoals ze gemeten werden in het laboratorium. We zien telkens een lichte afwijkingen in de gemeten golflengte van de spectraallijnen (de golflengten worden aangegeven boven of onder de spectra). Alle corresponderende spectraallijnen tussen het referentiespectrum en de gemeten spectra zijn aangegeven met een blauwe pijl, waarbij we ook de afwijking ($\Delta$) hebben aangegeven. In het bovenste spectrum is de tweede spectraallijn uit het referentiespectrum door een meetfout als het ware verdubbeld. In het onderste spectrum duikt op golflengte 524.8 nm een extra spectraallijn op.
Opgave
In deze opgave stellen we het emissiespectrum van een atoom of een chemische stof voor als een tuple met floating point getallen. Deze getallen stellen de golflengten van de spectraallijnen in het emissiespectrum voor, en moeten altijd in oplopende volgorde gerangschikt zijn.
Als we de referentiespectra van een reeks atomen opslaan in een bestand, dan doen we dat door op elke regel de symbolische naam van het atoom te zetten, gevolgd door een tab en de golflengten van de spectraallijnen in het emissiespectrum van dat atoom. De golflengten van de spectraallijnen worden van elkaar gescheiden door komma's (,). Hierbij moeten de golflengten niet noodzakelijk in oplopende volgorde gerangschikt zijn. Bij wijze van voorbeeld tonen we hieronder de inhoud van het bestand spectra.txt.
H 486.135,434.0472,656.279,410.1734 He 501.56783,667.8151,587.5621,471.31457,492.19313,504.7738,447.14802,438.79296,402.61914,412.08154 Li 610.354,670.791,413.259,610.365,670.776 Hg 404.6565,407.7837,434.74945,435.8335,535.4034,546.075,567.581,576.961,579.067,580.3782,585.9254,671.634,690.746
Gevraagd wordt:
- Schrijf een functie referentiespectra waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit tekstbestand moet de referentiespectra bevatten van een reeks atomen. De functie moet een dictionary teruggeven die de symbolische naam van elk atoom uit het bestand afbeeldt op zijn referentiespectrum. Een referentiespectrum wordt hierbij voorgesteld als een tuple dat de golflengten van de spectraallijnen uit het referentiespectrum bevat, voorgesteld als floating point getallen en gerangschikt in oplopende volgorde.
- Schrijf een functie referentielijnen waaraan twee emissiespectra moeten doorgegeven worden. Het eerste spectrum stelt een gemeten spectrum voor en het tweede een referentiespectrum. De functie heeft ook nog een derde optionele parameter eps waaraan een floating point waarde $\epsilon$ kan doorgegeven worden (standaardwaarde: 0.1). De waarde $\epsilon$ stelt de toegelaten afwijking voor tussen corresponderende spectraallijnen in de twee gegeven spectra. De functie moet een natuurlijk getal teruggeven, dat aangeeft hoeveel spectraallijnen in het referentiespectrum minstens één corresponderende spectraallijn hebben in het gemeten spectrum. Een spectraallijn met golflengte $g_r$ in het referentiespectrum correspondeert met een spectraallijn met golflengte $g_m$ in het gemeten spectrum als $|g_r - g_m| \leq \epsilon$.
- Schrijf een functie decompositie waaraan twee argumenten moeten doorgegeven worden: een gemeten spectrum en een dictionary met referentiespectra. De dictionary moet dezelfde vorm hebben als de dictionaries die worden teruggegeven door de functie referentiespectra. De functie heeft ook nog een optionele parameter eps die dezelfde betekenis en standaardwaarde heeft als bij de functie referentielijnen. De functie heeft ook nog een optionele parameter minimum waaraan een natuurlijk getal kan doorgegeven worden. De functie moet een alfabetisch gerangschikte lijst teruggeven van de symbolische namen van alle atomen die voorkomen in de gegeven dictionary, en waarvoor het corresponderende referentiespectrum "voldoende" corresponderende spectraallijnen heeft met het gemeten spectrum. Om het aantal corresponderende spectraallijnen te bepalen tussen het gemeten spectrum en een referentiespectum moet gebruik gemaakt worden van de functie referentielijnen en van de waarde die werd doorgegeven aan de parameter eps. Indien er expliciet een waarde werd doorgegeven aan de parameter minimum, dan geeft deze waarde het minimaal aantal corresponderende spectraallijnen aan dat als "voldoende" beschouwd wordt. Indien er niet expliciet een waarde werd doorgegeven aan de parameter minimum, dan zijn er pas "voldoende" corresponderende spectraallijnen, als alle spectraallijnen uit het referentiespectrum een corresponderende spectraallijn hebben in het gemeten spectrum.
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand spectra.txt zich in de huidige directory bevindt.
>>> referentiespectrum = referentiespectra('spectra.txt') >>> referentiespectrum['H'] (410.1734, 434.0472, 486.135, 656.279) >>> referentiespectrum['Li'] (413.259, 610.354, 610.365, 670.776, 670.791) >>> spectrum1 = (410.1055, 434.1126, 434.1427, 486.3071, 656.224) >>> referentielijnen(spectrum1, referentiespectrum['H']) 3 >>> spectrum2 = (410.1875, 434.0906, 486.2315, 524.7571, 656.2779) >>> referentielijnen(spectrum2, referentiespectrum['H'], eps=0.1) 4 >>> referentielijnen(spectrum2, referentiespectrum['H'], eps=0.025) 2 >>> spectrum = (402.5579, 410.1914, 413.162, 434.1243, 486.0598, 504.7387, 610.157, 610.562, 656.354, 670.578, 670.991) >>> decompositie(spectrum, referentiespectrum) ['H'] >>> decompositie(spectrum, referentiespectrum, eps=0.2) ['H', 'Li'] >>> decompositie(spectrum, referentiespectrum, minimum=2) ['H', 'He'] >>> decompositie(spectrum, referentiespectrum, eps=0.2, minimum=2) ['H', 'He', 'Li']
| Added by: | Peter Dawyndt |
| Date: | 2015-01-30 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS