SPOJ.com - Problem PROG0533

PROG0533 - Recombination

no tags

Recombination is a general process in which multi-component entities physically interact and mutually exchange components to create chimeric products or offspring. While the concept is most often applied to the heredity actions that occur in the living world, parallels exist in chemistry, physics, engineering, and many other scientific disciplines. A simple instance of recombination can be symbolized as: $$ A\bullet B + C\bullet D \longrightarrow A\bullet D + C\bullet B $$ where $A$, $B$, $C$ and $D$ represent potentially swappable components, the symbol $\bullet$ represents a concrete connection or bond between the components, and $A\bullet B, C\bullet D, \ldots$ represent complete entities with some sort of ascribable value in the system. In the realm of chemical physics for example, one can describe the process of nucleosynthesis as the recombination of existing nuclei to generate new ones. In the realm of biology, recombination of existing genes or genomes can create theretofore novel genotypes. In any event, a characteristic feature of recombination is that relatively large blocks of an underlying material are exchanged among individuals, rather than an alternative process in which new whole entities are made by piecing together minimal subunits, one-at-a-time. If each block contains quantifiable information, then the complexity of the system as a whole can be significantly affected by recombination events.

Assignment

Recombination may also be applied to natural language. If we start with two words that have equal length, recombination can be defined as the process in which corresponding sequences of one or more successive letters are exchanged between these two words. Accidentally, such a recombination might result in two existing words. Say, for example, that we start from the following two words:

BURGUL: cereal food made from the groats of several different wheat species, most often from durum wheat
AENEAS: Trojan hero in Greco-Roman mythology, son of the prince Anchises and the goddess Venus (Aphrodite)

If we then number the positions of the letters in the words from left to right, starting at 1, and exchange the letters at positions 2, 3 and 5, we get two other existing words:

BENGAL: geographical and ethno-linguistic region in South Asia
AUREUS: gold coin of ancient Rome valued at 25 silver denarii

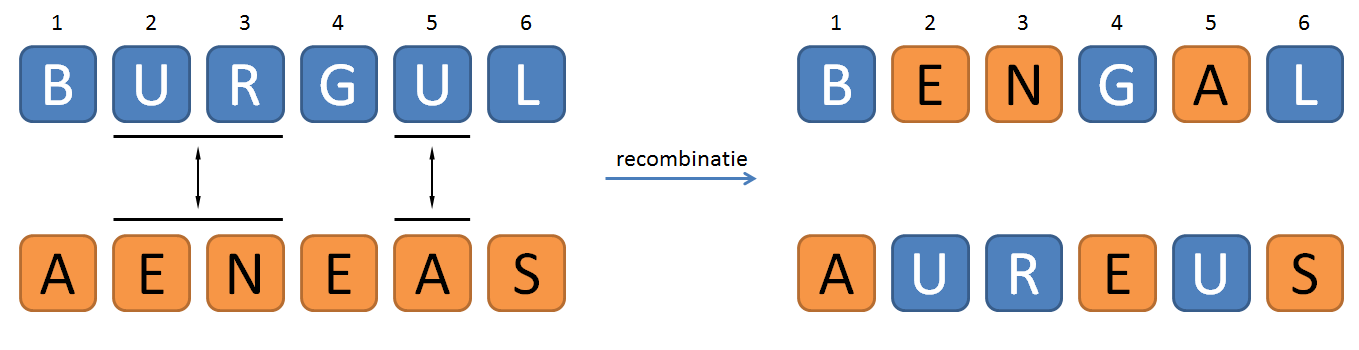
This recombination of the words BURGUL and AENEAS may be represented as

In this exercise we only consider words that contain letters. Your task is to write two functions that each take two or three words. All words passed to one of these functions should have equal length. If this is not the case, the functions must raise an AssertionError with the message words must have equal length. Raising this AssertionError always takes precedence over any other exceptions that are explicitly raised by the functions.

Write a function recombination that takes three words. If the third word can result from a recombination between the first two words, the function must return the other word that results from this recombination. In case the third word can not result from a recombination between the first two words, the function must raise an AssertionError with the message invalid recombination.
Write a function chimeras that takes three arguments. The first two arguments are words. The function must return a tuple containing the two words that result after recombination of the two given words. The third argument is a string that describes the fragments that must be exchanged during this recombination. Each fragment is a sequence of one or more consecutive letters that is described as m-n, with m being the start position of the sequence and n its final position. Positions of the letters in a word are numbered from left to right, starting at 1. The fragments are separated from each other by semicolons (;). A fragment that only contains a single letter is not represented as n-n, but simply as n.

Example

>>> recombination('burgul', 'aeneas', 'bengal')
'aureus'
>>> recombination('oleins', 'arcade', 'oreads')
'alcine'
>>> recombination('alevin', 'elodea', 'alodia')
'eleven'

>>> recombination('nitrogen', 'fluorine', 'tin')
Traceback (most recent call last):
AssertionError: words must have equal length
>>> recombination('nitrogen', 'fluorine', 'aluminium')
Traceback (most recent call last):
AssertionError: words must have equal length

>>> recombination('nitrogen', 'fluorine', 'ringtone')
Traceback (most recent call last):
AssertionError: invalid recombination

>>> chimeras('burgul', 'aeneas', '2-3;5')
('bengal', 'aureus')
>>> chimeras('oleins', 'arcade', '2;4-5')
('oreads', 'alcine')
>>> chimeras('alevin', 'elodea', '2-4;6')
('alodia', 'eleven')

>>> chimeras('nitrogen', 'aluminium', '3-7')
Traceback (most recent call last):
AssertionError: words must have equal length

Resources

Lehman N, Díaz Arenas C, White WA, Schmidt FJ (2011). Complexity through recombination: from chemistry to biology. Entropy 13(1), 17-37.

Recombinatie is een algemeen proces waarbij entiteiten die bestaan uit meerdere componenten, fysiek met elkaar interageren en daarbij componenten uitwisselen om chimerische producten of nakomelingen te maken. Hoewel het concept meestal wordt geassocieerd met overervingsstappen die voorkomen bij levende organismen, bestaan er ook parallellen in de chemie, fysica, bouwkunde en vele andere wetenschappelijke disciplines. Een eenvoudig voorbeeld van recombinatie kan voorgesteld worden als: $$ A\bullet B + C\bullet D \longrightarrow A\bullet D + C\bullet B $$ waarbij $A$, $B$, $C$ en $D$ uitwisselbare componenten voorstellen, het symbool $\bullet$ staat voor een connectie of binding tussen de componenten, en $A\bullet B, C\bullet D, \ldots$ de volledige entiteiten voorstellen. Het proces van nucleosynthese uit het domein van de chemische fysica kan bijvoorbeeld beschreven worden als de recombinatie van bestaande kernen waaruit nieuwe kernen gevormd worden. In de biologie kunnen nieuwe genotypes ontstaan door recombinatie van bestaande genen of genomen. In al deze gevallen is een kenmerk van recombinatie dat relatief grote blokken van een onderliggend materiaal uitgewisseld worden tussen individuen, in plaats van een alternatief proces waarbij nieuwe entiteiten gevormd worden door minimale bouwstenen één voor één aan elkaar te zetten.

Opgave

Recombinatie kan ook toegepast worden op natuurlijke taal. Als we vertrekken van twee woorden die even lang zijn, dan is recombinatie het proces waarbij overeenkomstige reeksen van één of meer opeenvolgende letters uitgewisseld worden tussen de twee woorden. Heel af en toe resulteert een dergelijke recombinatie in twee bestaande woorden. Stel dat we bijvoorbeeld vertekken van de volgende twee Engelse woorden:

BURGUL: graanproduct gemaakt van verschillende soorten tarwe, maar meestal van durum (harde tarwe); de tarwekorrels worden eerst gestoomd, daarna gedroogd en vervolgens gemalen of gebroken
AENEAS: mythologische Trojaanse held, zoon van de sterfelijke prins Anchises en de godin Venus (Aphrodite)

Als we nu de posities van de letters in de woorden van links naar rechts nummeren vanaf 1, dan krijgen we na uitwisseling van de letters op de posities 2, 3 en 5 twee andere bestaande Engelse woorden met de volgende betekenis:

BENGAL: regio in het noordoosten van het Indisch Subcontintent die is onderverdeeld in de Indiase staat West-Bengalen en het land Bangladesh; geldt als één van de dichtstbevolkte gebieden op Aarde
AUREUS: gouden munt ter waarde van 25 denarii die gebruikt werd in het Romeinse Rijk

Deze recombinatie van de woorden BURGUL en AENEAS kan voorgesteld worden als

In deze opgave werken we met woorden die enkel bestaat uit letters. Gevraagd wordt om de volgende twee functies te schrijven, waaraan telkens twee of drie woorden moeten doorgegeven worden. Hierbij moet telkens gelden dat alle opgegeven woorden dezelfde lengte hebben. Indien dit niet het geval is, dan moeten de functies een AssertionError opwerpen met de boodschap woorden moeten even lang zijn. Het opwerpen van deze AssertionError krijgt telkens voorrang op eventuele andere exceptions die expliciet door de functies opgeworpen worden.

Schrijf een functie recombinatie waaraan drie woorden moeten doorgegeven worden. Als het derde woord kan ontstaan zijn na recombinatie van de eerste twee woorden, dan moet de functie het andere woord teruggeven dat ontstaan is na diezelfde recombinatie. Indien het derde woord niet kan ontstaan zijn na recombinatie van de eerste twee woorden, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige recombinatie.
Schrijf een functie chimeren waaraan drie argumenten moeten doorgegeven worden. De eerste twee argumenten zijn woorden. De functie moet een tuple teruggeven dat de twee woorden bevat die ontstaan na recombinatie van de twee gegeven woorden. Het derde argument is een string die de fragmenten omschrijft die bij deze recombinatie moeten uitgewisseld worden. Hierbij is elk fragment een reeks van één of meer opeenvolgende letters die wordt omschreven als m-n waarin m de positie van de eerste letter in de reeks aangeeft en n de positie van de laatste letter ervan. De posities van de letters in een woord worden van links naar rechts genummerd vanaf 1. De verschillende fragmenten worden van elkaar gescheiden door een puntkomma (;). Een fragment dat slechts uit één letter bestaat wordt niet genoteerd als n-n, maar simpelweg als n.

Voorbeeld

>>> recombinatie('burgul', 'aeneas', 'bengal')
'aureus'
>>> recombinatie('oleins', 'arcade', 'oreads')
'alcine'
>>> recombinatie('alevin', 'elodea', 'alodia')
'eleven'

>>> recombinatie('nitrogen', 'fluorine', 'tin')
Traceback (most recent call last):
AssertionError: woorden moeten even lang zijn
>>> recombinatie('nitrogen', 'fluorine', 'aluminium')
Traceback (most recent call last):
AssertionError: woorden moeten even lang zijn

>>> recombinatie('nitrogen', 'fluorine', 'ringtone')
Traceback (most recent call last):
AssertionError: ongeldige recombinatie

>>> chimeren('burgul', 'aeneas', '2-3;5')
('bengal', 'aureus')
>>> chimeren('oleins', 'arcade', '2;4-5')
('oreads', 'alcine')
>>> chimeren('alevin', 'elodea', '2-4;6')
('alodia', 'eleven')

>>> chimeren('nitrogen', 'aluminium', '3-7')
Traceback (most recent call last):
AssertionError: woorden moeten even lang zijn

Bronnen

Lehman N, Díaz Arenas C, White WA, Schmidt FJ (2011). Complexity through recombination: from chemistry to biology. Entropy 13(1), 17-37.

Submit solution!

Added by:	Peter Dawyndt
Date:	2015-01-27
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None