PROG0512 - Doomsday clock
The Doomsday Clock is a universally-recognized symbolic clock face, representing a countdown to possible political related global catastrophe (nuclear war or climate change). It has been maintained since 1947 by the members of the Science and Security Board of the Bulletin of the Atomic Scientists, who are in turn advised by the Governing Board and the Board of Sponsors, including 18 Nobel Laureates. The closer they set the Clock to midnight, the closer the scientists believe the world is to global disaster. The Clock — which hangs on a wall in a Bulletin's office in the University of Chicago — originally represented an analogy for the threat of global nuclear war. However, since 2007 it has also reflected climate change and new developments in the life sciences and technology that could inflict irrevocable harm to humanity.
In 1947, during the Cold War, the Clock was started at seven minutes to midnight and was subsequently advanced or rewound per the state of the world and nuclear war prospects. The Clock is not set and reset in real time as events occur. Rather than respond to each and every crisis as it happens, the Science and Security Board meets twice annually to discuss global events in a deliberative manner. The closest nuclear war threat, the Cuban Missile Crisis in 1962, reached crisis, climax, and resolution before the Clock could be set to reflect that possible doomsday. In 1991 the Clock was set seventeen minutes before midnight as the United States and the Soviet Union signed the Strategic Arms Reduction Treaty, after which the Soviet Union dissolved. This is the Clock's earliest setting since its inception.
The Doomsday Clock also works a barometer that indicates how positive people saw the future at certain times in recent history, as evidenced by the 1969 hit song In the Year 2525 (Exordium et Terminus) by the American pop-rock duo Zager & Evans.
Assignment
In this exercise, progress of the Doomsday Clock is represented as a string having the following format.
1947 7,1949 3,1953 2,1960 7,1963 12,1968 7,1969 10,1972 12,1974 9,1980 7,1981 4,1983 3,1984 3
This string representation contains a comma-separated sequence of Clock adjustments. Each adjustment is described as the year in which the Clock was reset, followed by a space and the minutes before midnight to which the Clock was set. The Clock adjustments are listed in chronological order, and you may assume that the Clock is never reset twice a year.
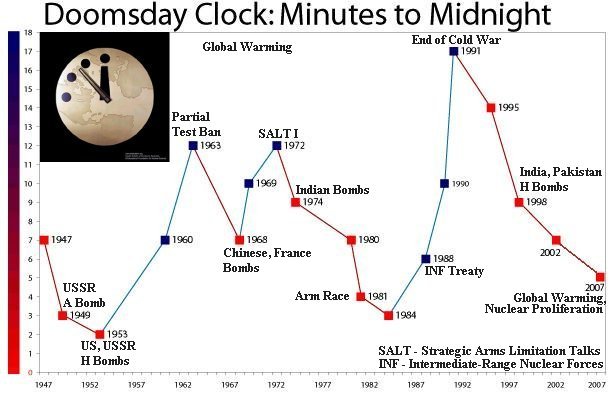
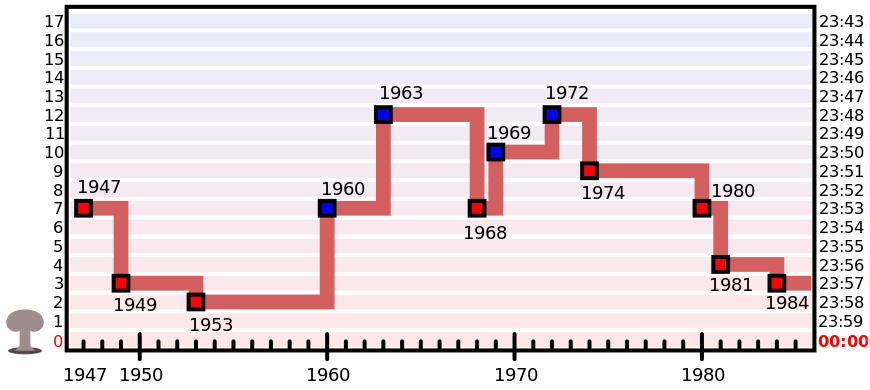
The figure below shows a graphical representation of the string representation shown above. If we represent time on a 24-hour clock, it's easy to see from the figure that the Doomsday Clock for example was set to 23:57 in 1950, to 23:48 in 1965 and to 23:51 in 1974. We will always consider the adjusted time in years where the clock was reset.
The goal of this exercise is to determine the threat in a given year, given the progress of the Doomsday Clock. This threat is expressed as a timestamp on a 24-hour clock. Your task:
- Write a function clock that takes a positive integer. This integer expresses a given number of minutes before midnight. The function must return a string containing the representation of that time stamp on a 24-hour clock, using the format hh:mm. This implies that $0 \leq \text{hh} < 24$ and $0 \leq \text{mm} < 60$.
- Write a function progress that takes the string representation of the progress of the Doomsday Clock, formatted as described in the introduction of this assignment. The function must return the progress of the Clock as a tuple of tuples, where each adjustment to the Clock is represented as a tuple whose first element is the year (integer) the clock was reset and whose second element is the time to which the Clock was set (string representation on a 24-hour clock, as generated by the function clock).
- Write a function threat that takes two arguments: an integer representing a given year and a tuple of tuples representing the progress of the Doomsday Clock in the format returned by the function progress. The function must return the time indicated by the Clock in the given year, represented on a 24-hour clock. You may assume that the given year is always included in the interval in which the given progress of the Doomsday Clock is described, including the limits.
Example
>>> clock(0) '00:00' >>> clock(7) '23:53' >>> clock(123) '21:57' >>> adjustments = '1947 7,1949 3,1953 2,1960 7,1963 12,1968 7,1969 10,1972 12,1974 9,1980 7,1981 4,1983 3,1984 3' >>> doomsdayclock = progress(adjustments) >>> doomsdayclock ((1947, '23:53'), (1949, '23:57'), (1953, '23:58'), (1960, '23:53'), (1963, '23:48'), (1968, '23:53'), (1969, '23:50'), (1972, '23:48'), (1974, '23:51'), (1980, '23:53'), (1981, '23:56'), (1983, '23:57'), (1984, '23:57')) >>> threat(1974, doomsdayclock) '23:51' >>> threat(1950, doomsdayclock) '23:57' >>> threat(1965, doomsdayclock) '23:48'
De doemdagklok (Engels: Doomsday Clock) is een symbolische klok die sinds 1947 aan de Universiteit van Chicago wordt bijgehouden door de Bulletin of the Atomic Scientists. De klok geeft aan hoe dicht de mensheid bij een kernoorlog staat. Dit wordt voorgesteld als een aantal minuten voor middernacht, waarbij middernacht symbool staat voor het uitbreken van een kernoorlog. Het aantal minuten voor middernacht is hierbij dus een maat voor nucleaire dreiging.
Telkens wanneer gebeurtenissen op het wereldtoneel de dreiging versterken of verzwakken, wordt de klok bijgewerkt. In 1953 werd de klok bijvoorbeeld op twee voor twaalf gezet toen de VS en de Sovjet-Unie allebei testen begonnen uit te voeren met waterstofbommen. In 1991 werd de klok op zeventien minuten voor twaalf gezet, ten gevolge van het toenmalige akkoord tussen de VS en de Sovjet-Unie over het terugdrijven van hun kernwapenarcenaal. Onderstaande grafiek toont het verloop van de klok doorheen de recente geschiedenis:
De doemdagklok is ook een goeie barometer om aan te geven hoe positief men de toekomst inzag op bepaalde momenten in het recente verleden, zoals blijkt uit de hit In the Year 2525 (Exordium et Terminus) die het Amerikaanse pop-rock duo Zager & Evans uitbracht in 1969.
Opgave
Bij deze opgave wordt het verloop van de doemdagklok voorgesteld door een string van de vorm
1947 7,1949 3,1953 2,1960 7,1963 12,1968 7,1969 10,1972 12,1974 9,1980 7,1981 4,1983 3,1984 3
Hierbij worden een reeks klokaanpassingen opgelijst, die telkens van elkaar worden gescheiden door een komma. Elke aanpassing wordt beschreven door het jaartal waarin de klok werd bijgesteld, gevolgd door een spatie en het nieuwe aantal minuten voor middernacht waarop de klok werd ingesteld. De klokaanpassingen worden in chronologische volgorde opgelijst, en je mag ervan uitgaan dat de doemsdagklok nooit tweemaal wordt bijgesteld in hetzelfde jaar.
Onderstaande figuur toont een grafische voorstelling van de stringvoorstelling die hierboven als voorbeeld werd gegeven. Als we tijdstippen voorstellen op een 24-uursklok, dan kun je uit de figuur makkelijk aflezen dat de doemdagklok bijvoorbeeld in 1950 ingesteld stond op 23:57, in 1965 op 23:48 en in 1974 op 23:51. We zullen altijd de nieuwe stand van de klok beschouwen in een jaar waarin de klok werd bijgesteld.
Het doel van deze opgave is om de dreiging te bepalen in een gegeven jaar, op basis van een gegeven verloop van de doemdagklok. Deze dreiging moet uitgedrukt worden als een tijdstip op een 24-uursklok. Gevraagd wordt:
- Schrijf een functie klok waaraan een natuurlijk getal moet doorgegeven worden. Dit getal stelt een gegeven aantal minuten voor middernacht voor. De functie moet een string teruggeven die de weergave bevat van het corresponderende tijdstip op een 24-uursklok, in het formaat uu:mm. Hierbij moet dus gelden dat $0 \leq \text{uu} < 24$ en $0 \leq \text{mm} < 60$.
- Schrijf een functie verloop waaraan de stringvoorstelling van het verloop van de doemdagklok moeten doorgegeven worden, in het formaat zoals aangegeven in de inleiding. De functie moet het verloop van de doemdagklok teruggeven als een tuple van tuples, waarbij elke aanpassing aan de klok wordt beschreven als een tuple met als eerste element het jaartal (als natuurlijk getal) waarin de aanpassing gebeurde, en als tweede element het tijdstip waarop de klok werd ingesteld (stringvoorstelling op een 24-uursklok, zoals gegenereerd door de functie klok).
- Schrijf een functie dreiging waaraan twee argumenten moeten doorgegeven worden: een natuurlijk getal dat een jaartal voorstelt, en een tuple van tuples dat het het verloop van de doemdagklok voorstelt in het formaat zoals dat wordt weergegeven door de functie verloop. De functie moet het tijdstip teruggeven waarop de klok staat ingesteld in het gegeven jaartal, weergegeven op een 24-uursklok. Je mag ervan uitgaan dat het gegeven jaartal altijd binnen het interval ligt waarin het verloop van de doemdagklok wordt beschreven, inclusief de uiterste grenzen.
Voorbeeld
>>> klok(0) '00:00' >>> klok(7) '23:53' >>> klok(123) '21:57' >>> aanpassingen = '1947 7,1949 3,1953 2,1960 7,1963 12,1968 7,1969 10,1972 12,1974 9,1980 7,1981 4,1983 3,1984 3' >>> doemdagklok = verloop(aanpassingen) >>> doemdagklok ((1947, '23:53'), (1949, '23:57'), (1953, '23:58'), (1960, '23:53'), (1963, '23:48'), (1968, '23:53'), (1969, '23:50'), (1972, '23:48'), (1974, '23:51'), (1980, '23:53'), (1981, '23:56'), (1983, '23:57'), (1984, '23:57')) >>> dreiging(1974, doemdagklok) '23:51' >>> dreiging(1950, doemdagklok) '23:57' >>> dreiging(1965, doemdagklok) '23:48'
| Added by: | Peter Dawyndt |
| Date: | 2014-10-16 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS