PROG0508 - Smoke signals
In Ancient China, soldiers stationed along the Great Wall would alert each other of impending enemy attack by signaling from tower to tower. In this way, they were able to transmit a message as far away as 750 kilometers in just a few hours.
The fortifications along the Great Wall of China are not positioned in a straight line, but form a network of walls made of stone, brick, tampered earth and wood that connect a series of watchtowers with each other. Watchtowers used to spread smoke signals are usually built on top of a hummock to optimize the observation of the signals.
Assignment
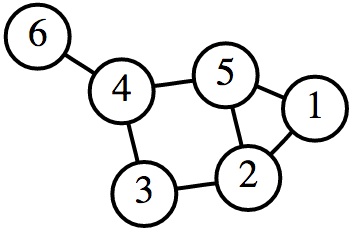
An example netwerk of guard posts along the Great Wall of China where smoke signals can be released is depicted below. The guard posts are represented as circles, with each watchtower labeled by an integer. Two watchtowers are connected by a line if smoke signals released from one of the towers can be observed at the other watchtower. As such, a smoke signal released at watchtower 6 in this network can be observed only at watchtower 4. A smoke signal released at watchtower 1 can be observed at watchtowers 2 and 5. As soon as a guard post observes a smoke signal, it starts releasing smoke signals at its own watchtower in order to spread the alarm along the entire network.
In this exercise, each watchtower is represented by an integer that uniquely identifies the guard post. A network of guard posts is represented as a dictionary, whose keys are formed by the set of all watchtowers in the network. The dictionary maps each key onto a set of integers, that represent the neighbours of the key (watchtower) in the network. The example network depicted above is thus represented by the following dictionary:
{1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}}
Your task:
- Write a function observed that takes two arguments: a set of watchtowers where smoke signals are released and a dictionary representing a network of watchtowers. The function must return the set of watchtowers in the network where smoke signals are observed by that do not release smoke signals themselves.
- Use the function observed to write a function distribution that takes two arguments: a watchtower (integer) and a dictionary representing a network of watchtowers. At time zero, a smoke signal is released at the given watchtower. After each time step additional smoke signals are released at all watchtowers where a smoke signal is observed. The function must return an integer that indicates after how many time steps the alarm has been spread across all watchtowers in the network.
Example
>>> network = {1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}} >>> observed({1, 2}, network) {3, 5} >>> observed({3, 4}, network) {2, 5, 6} >>> distribution(1, network) 3 >>> distribution(4, network) 2
In het oude China verzonden soldaten die gestationeerd waren langs de Chinese Muur rooksignalen van toren naar toren om de aantocht van vijandelijke troepen aan elkaar door te seinen. Op die manier konden boodschappen zich in een paar uur tijd verspreiden over een afstand van meer dan 750 kilometer.
De verdedigingslinie die door de Chinese Muur werd opgetrokken vormde geen rechte lijn, maar een netwerk van aarden en stenen versterkingen die verschillende wachtposten met elkaar verbonden. Wachtposten die gebruikt werden om rooksignalen te verspreiden, waren doorgaans op een hoogte gebouwd om het waarnemen van de signalen zo optimaal mogelijk te laten verlopen.
Opgave
Hieronder hebben we een voorbeeld getekend van een netwerk van wachtposten langs de Chinese Muur waarop rooksignalen kunnen opgelaten worden. De wachtposten worden voorgesteld door cirkels, en elke wachtpost wordt op een unieke manier gelabeld door een natuurlijk getal. Twee wachtposten worden door een lijn met elkaar verbonden als de rooksignalen die worden opgelaten vanaf de ene wachttoren kunnen waargenomen worden op de andere wachttoren. Zo zie je dat in dit netwerk een rooksignaal dat wordt opgelaten vanaf wachttoren 6 enkel kan waargenomen worden op wachttoren 4. Een rooksignaal dat wordt opgelaten vanaf wachttoren 1 kan worden waargenomen op wachttorens 2 en 5. Van zodra door een wachtpost een rooksignaal wordt waargenomen, begint men vanaf die wachttoren ook rooksignalen op te laten om zo de waarschuwing te verspreiden langs het volledige netwerk.
In deze opgave wordt elke wachtpost voorgesteld door een natuurlijk getal, dat gebruikt wordt om de wachtpost te identificeren. Een netwerk van wachtposten wordt voorgesteld als een dictionary, waarin alle wachttorens als sleutel voorkomen. Elke sleutel wordt door de dictionary afgebeeld op een verzameling natuurlijke getallen, die de labels voorstellen van de buren van de sleutel (wachttoren) in het netwerk. Het netwerk dat hierboven als voorbeeld gebruikt werd, wordt op deze manier beschreven door de volgende dictionary:
{1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}}
Gevraagd wordt:
- Schrijf een functie waargenomen waaraan twee argumenten moeten doorgegeven worden: een verzameling wachtposten waarvan een rooksignaal wordt opgelaten en een dictionary die een netwerk van wachtposten voorstelt. De functie moet de verzameling wachtposten in het netwerk teruggeven waarop een rooksignaal wordt waargenomen maar waarvan zelf geen rooksignaal wordt opgelaten.
- Gebruik de functie waargenomen om een functie verspreiding te schrijven waaraan twee argumenten moeten doorgegeven worden: een wachtpost (integer) en een dictionary die een netwerk van wachtposten voorstelt. Op tijdstip nul wordt een rooksignaal opgelaten vanaf de gegeven wachttoren. Na elke tijdsstap worden bijkomende rooksignalen opgelaten vanaf alle wachttorens waarop een rooksignaal wordt waargenomen. De functie moet een natuurlijk getal teruggeven dat aangeeft na hoeveel tijdsstappen het signaal verspreid werd over alle wachttorens in het netwerk.
Voorbeeld
>>> netwerk = {1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}} >>> waargenomen({1, 2}, netwerk) {3, 5} >>> waargenomen({3, 4}, netwerk) {2, 5, 6} >>> verspreiding(1, netwerk) 3 >>> verspreiding(4, netwerk) 2
| Added by: | Peter Dawyndt |
| Date: | 2014-10-15 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS