PROG0487 - The stopped clock
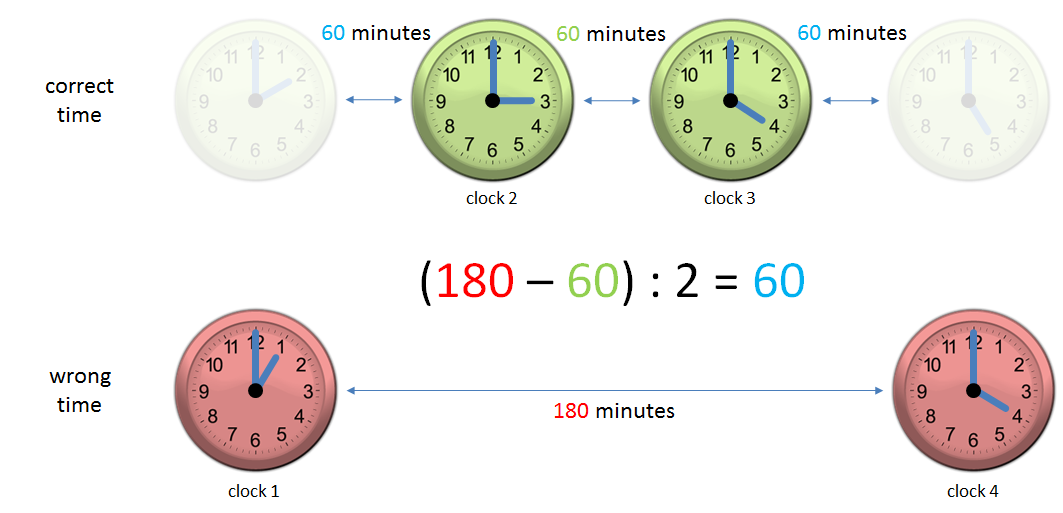
Andrea's only timepiece is a large grandfather clock that is fixed to the wall. One day she forgets to wind it and it stops. A few days later, she travels across town to have dinner with a friend whose own clock is always correct. When she returns home, she makes a simple calculation and sets her own clock accurately. How does she manage this without knowing the travel time between her house and her friend's?
Before she leaves the house, Andrea winds her own clock and sets it to an arbitrary time. Then she notes the correct time at her friend's house both when she arrives and when she leaves. When she returns home she consults her own clock to see how much time the whole trip has taken, subtracts the period she spent at her friend's house, and divides the result by two to learn the travel time in each direction. By adding this interval to the time she noted as she left her friend's house, she can infer the current time and set her own clock.
Input
The input consists of 8 integers. Each pair of consecutive integers $h$ ($0 \leq h < 24$) and $m$ ($0 \leq m < 60$) corresponds to the timestamp $h:m$ on a 24-hour-clock. The four timestamps consecutively indicate the time at which Andrea
- leaves her own house
- arrives at her friend's house
- leaves her friend's house
- returns to her own house
Output
Two lines containing the integers $h$ ($0 \leq h < 24$) and $m$ ($0 \leq m < 60$) that correspond to the correct time $h:m$ on a 24-hour-clock when Andrea returns to her own house. You may assume that the total time Andrea is away from home is at most 24 hours.
Example
Input:
13
0
15
0
16
0
16
0
Output:
17
0
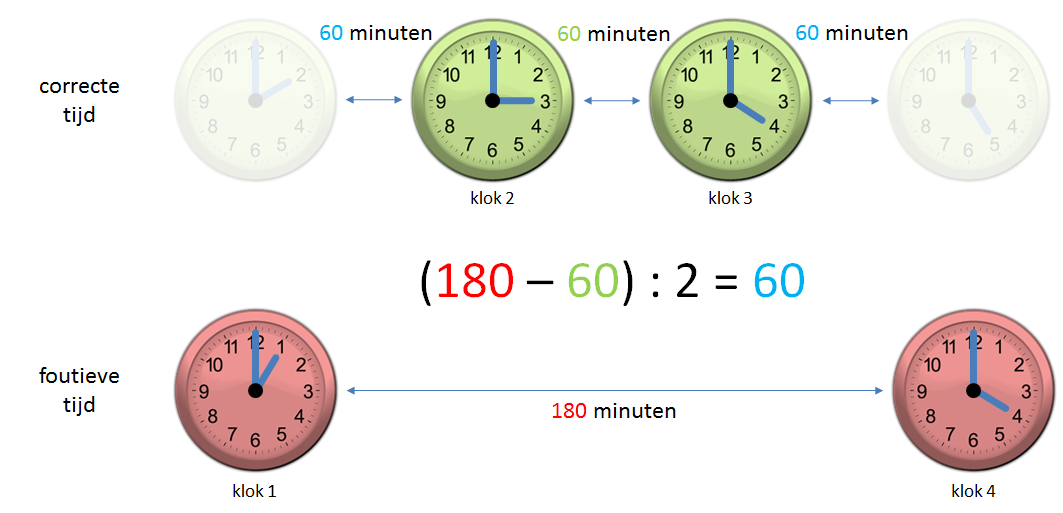
Het enige uurwerk dat Andrea in huis heeft, is een grote staande klok. Op een dag is ze vergeten om de klok op te winden, waardoor de klok gestopt is met tikken. Enkele dagen later reist ze naar de stad om er te gaan lunchen bij een vriendin wiens klok altijd de correcte tijd aangeeft. Als ze terug thuiskomt, maakt ze een eenvoudige berekening waarmee ze haar klok terug juist kan zetten. Hoe is ze daarin geslaagd zonder de exacte reistijd te kennen tussen haar huis en dat van haar vriendin?
Vooraleer haar huis te verlaten, windt Andrea haar staande klok terug op en onthoudt ze de tijd die de klok bij vertrek aangeeft. Daarna onthoudt ze ook de correcte tijd die de klok in het huis van haar vriendin aangeeft, zowel bij aankomst als bij vertrek. Als ze terug thuiskomt, kan ze op basis van de tijd die haar klok aangeeft, bepalen hoeveel tijd de volledige trip geduurd heeft. Daar trekt ze de tijd vanaf die ze in het huis van haar vriendin heeft doorgebracht, en deelt het resultaat door twee om de reistijd tussen haar huis en dat van haar vriendin te weten te komen. Als ze deze tijdsduur optelt bij de tijd die de klok aangaf als ze bij het huis van haar vriendin vertrok, dan bekomt ze de huidige tijd waarmee ze haar eigen klok kan instellen.
Invoer
De invoer bestaat uit 8 natuurlijke getallen. Elk paar opeenvolgende getallen $h$ ($0 \leq h < 24$) en $m$ ($0 \leq m < 60$) correspondeert met de tijdsaanduiding $h:m$ op een 24-uursklok. De vier tijdsaanduidingen geven achtereenvolgens de tijd aan op het ogenblik dat Andrea
- vertrekt vanaf haar eigen huis
- aankomt bij het huis van haar vriendin
- terug vertrekt vanaf het huis van haar vriendin
- terug aankomt bij haar eigen huis
Uitvoer
Twee regels die de natuurlijke getallen $h$ ($0 \leq h < 24$) en $m$ ($0 \leq m < 60$) bevatten die corresponderen met de correcte tijd $h:m$ op een 24-uursklok wanneer Andrea terug aankomt bij haar eigen huis. Je mag ervan uitgaan dat Andrea niet langer dan 24 uur van huis is weggeweest.
Voorbeeld
Invoer:
13
0
15
0
16
0
16
0
Uitvoer:
17
0
| Added by: | Peter Dawyndt |
| Date: | 2014-08-23 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS