PROG0479 - The mechanical Internet
Telecommunications got an early start in France, where inventor Claude Chappe built a series of towers between Lille and Paris in 1792. Each tower was topped with a set of movable wooden arms that could be arranged to represent symbols. If each operator viewed his neighbor through a telescope, a symbol could pass through 15 stations covering 120 miles in only 9 minutes, giving France a valuable communications advantage over the surrounding powers during the sensitive period of the revolution.
This mechanical form of the Internet avant la lettre even makes an appearance in The Count of Monte-Cristo (Alexandre Dumas, 1844, original French title: Le Comte de Monte-Cristo):
They passed to the third story; it was the telegraph room. Monte Cristo looked in turn at the two iron handles by which the machine was worked. "It is very interesting," he said, "but it must be very tedious for a lifetime."
"Yes. At first my neck was cramped with looking at it, but at the end of a year I became used to it; and then we have our hours of recreation, and our holidays."
"Holidays?"
"Yes."
"When?"
"When we have a fog."
Expanded into a network of 534 stations, the system worked well, but it was expensive, with skilled operators manning towers set every 10-30 kilometers, and the messages were far from private. Finally the electrical telegraph killed it — Sweden abandoned the last commercial semaphore line in 1880. By then, depressed by illness and the conviction that others were stealing his ideas, Chappe had long since killed himself.
Assignment
- Write a function network that takes the location of a text file as its argument. This file describes a network of towers that may communicate with each other. Each line of the file contains the names of two neighboring towers (indicated by the name of the city where the towers are located), separated from each other by a tab. The function must return a dictionary that maps the name of each tower (city) in the network onto a set containing the names of its neighboring towers (cities).
- Write a function hubs that takes three arguments. The first two arguments are names of towers. The third argument is a dictionary that described the topology of a network of towers, formatted as the dictionaries returned by the function network. The function must return an integer that indicates the minimal number of times a symbol must be transmitted from one tower to a neighboring tower in the network, to sent the message between the two given towers. If a message cannot be sent between the two given towers — because they belong to two disconnected subnetworks — the function must return the value -1. If at least one of the given towers does not belong to the given network, an AssertionError must be raised with the message city not in network.
Algorithm
You can use the following algorithm to find the shortest path between tower1 and tower2 in a network:
- Initialize $U$ = [tower1] as a list of towers whose neighbors still need to be processed, and $P$ = {tower1:0} as a dictionary that maps each processed tower onto the shortest distance from that tower to tower1.
- Remove the first tower from $U$ and process its neighbors in the network by appending each unprocessed neighbor to $U$ and adding to $P$ the shortest distance from that unprocessed neighbour to tower1.
- Keep repeating step 2 until a neighbors is reached that equals tower2 (figure out yourself how to obtain the distance to tower1) or until $U$ is empty (meaning that tower2 could not be reached from tower1).
Unicode files
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems. The standard consists of a set of code charts for visual reference, an encoding method and set of standard character encodings, a set of reference data computer files, and a number of related items, such as character properties, rules for normalization, decomposition, collation, rendering, and bidirectional display order (for the correct display of text containing both right-to-left scripts, such as Arabic and Hebrew, and left-to-right scripts).
Unicode can be implemented by different character encodings. The most commonly used encodings are UTF-8, UTF-16 and the now-obsolete UCS-2. UTF-8 uses one byte for any ASCII character, all of which have the same code values in both UTF-8 and ASCII encoding, and up to four bytes for other characters. To open a Unicode file in Python, you can pass the encoding used to the optional parameter encoding of the built-in function open. For example, in order to read the information from the Unicode text file france.txt that makes use of UTF-8 encoding, the file can be opened in the following way:
>>> open('france.txt', 'r', encoding='utf-8')
Example
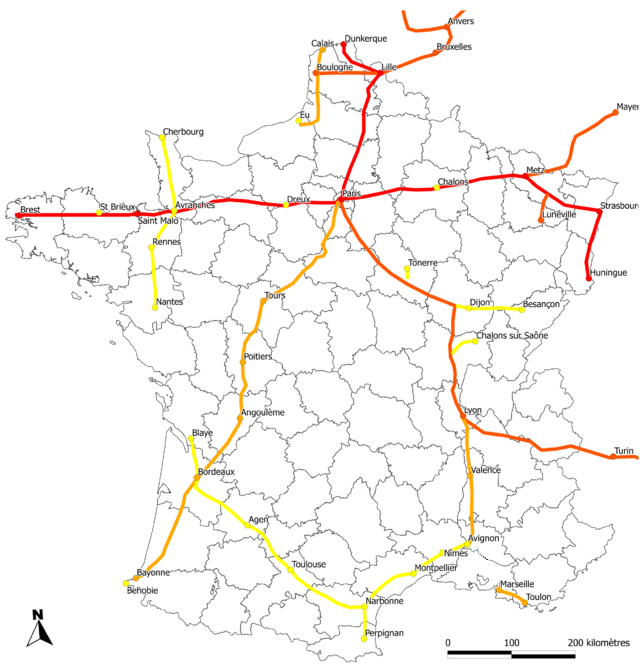
In the following interactive session we assume that the text file chappe.txt is in the current directory. This file contains a description of the network of towers that is graphically represented below. Note, for example, that the network has no connection between Avignon and Marseilles. As a result, no messages can be communicated between Lille and Marseille (they belong to two disconnected subnetworks).
>>> chappe = network('chappe.txt') >>> chappe['Lille'] {'Paris', 'Bruxelles', 'Dunkerque', 'Boulogne'} >>> chappe['Paris'] {'Tours', 'Dreux', 'Tonerre', 'Lille'} >>> chappe['Brest'] {'St Brieux'} >>> hubs('Lille', 'Lille', chappe) 0 >>> hubs('Lille', 'Tours', chappe) 2 >>> hubs('Lille', 'Toulouse', chappe) 11 >>> hubs('Lille', 'Montpellier', chappe) 9 >>> hubs('Lille', 'Perpignan', chappe) 11 >>> hubs('Lille', 'Marseille', chappe) -1 >>> hubs('Lille', 'Londres', chappe) Traceback (most recent call last): AssertionError: city not in network
Telecommunicatie kreeg in Frankrijk een vroege start toen uitvinder Claude Chappe in 1792 een reeks torens bouwde tussen Rijsel en Parijs. Bovenaan elke toren werd een constructie van beweegbare houten armen aangebracht. Deze armen konden zo geschikt worden dat ze een bepaald symbool voorstelden. Als de operatoren door middel van een telescoop de opstelling van naburige torens in de gaten hielden, dan kon een symbool in 9 minuten over de 15 torens langs het 200 kilometer lange traject doorgestuurd worden. Tijdens de gevoelige periode van de revolutie gaf deze vorm van communicatie aan Frankrijk een enorm voordeel tegenover de omliggende machten.
Deze mechanische vorm van het Internet avant la lettre kreeg bijvoorbeeld een vermelding in De graaf van Monte-Cristo (Alexandre Dumas, 1844, originele Franse titel: Le Comte de Monte-Cristo):
Ze gingen naar de derde verdieping en bereikten zo de kamer van de telegraaf. Monte Cristo keek heen en weer naar de twee ijzeren handvatten waarmee de machine bediend werd. "Dit is uiterst interessant", zei hij, "maar het lijkt me een zeer tijdrovende bezigheid."
"Ja. In eerste instantie kreeg ik steeds een stijve nek door ernaar te kijken. Maar naar het einde van het jaar toe begon ik eraan gewend te raken. En toen kregen we eerst een paar uur ontspanning, en daarna zelfs een heuse vakantie."
"Vakantie?"
"Ja"
"Wanneer?"
"Toen de mist begon op te komen."
De Chappe semafoorlijn groeide op zijn hoogtepunt uit tot een netwerk van 534 torens. Het systeem werkte zeer goed, maar was ontzettend duur door de nood aan goed opgeleide operatoren die om de 10-30 kilometer een toren moesten bemannen. Bovendien kon de berichtgeving moeilijk geheim gehouden worden.
De opkomst van de elektrische telegraaf betekende uiteindelijk het doodvonnis van de Chappe-lijn. Zweden doekte de laatste commerciële semafoorlijn op in 1880. Tegen die tijd had Claude Chappe — depressief door ziekte en de overtuiging dat anderen zijn idee hadden gestolen — zichzelf al lang van kant gemaakt.
Opgave
- Schrijf een functie netwerk waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit bestand beschrijft een netwerk van torens die met elkaar kunnen communiceren. Elke regel van het bestand bevat de namen van twee naburige torens (aangegeven met de naam van de stad waar de torens zich bevinden), van elkaar gescheiden door een tab. De functie moet een dictionary teruggeven, die de naam van elke toren (stad) in het netwerk afbeeldt op een verzameling met de namen van alle naburige torens (steden).
- Schrijf een functie tussenstations waaraan drie argumenten moeten doorgegeven worden. De eerste twee argumenten zijn namen van torens. Het derde argument is een dictionary dat de topologie van een netwerk van torens aangeeft, in de vorm zoals de dictionaries die worden teruggegeven door de functie netwerk. De functie moet een natuurlijk getal teruggeven, dat aangeeft hoeveel keer een symbool minimaal moet doorgestuurd worden van een toren naar een naburige toren in het netwerk, om het bericht door te sturen tussen de twee gegeven torens. Indien het bericht niet kan doorgestuurd worden tussen de twee gegeven torens — omdat die behoren tot twee subnetwerken die niet met elkaar verbonden zijn — dan moet de functie de waarde -1 teruggeven. Als minstens één van de gegeven torens niet tot het gegeven netwerk behoort, dan moet de functie een AssertionError opwerpen met de boodschap stad behoort niet tot netwerk.
Algoritme
Om de kortste route te vinden tussen toren1 en toren2 in een netwerk, kan je als volgt te werk gaan:
- Initialiseer $U$ = [toren1] als een lijst met torens waarvan de buren nog moeten verwerkt worden, en $P$ = {toren1:0} als een dictionary die elke verwerkte toren afbeeldt op de kortste afstand van die toren tot toren1.
- Verwijder de eerste toren uit $U$ en verwerk zijn buren in het netwerk door elke onverwerkte buur achteraan toe te voegen aan $U$ en de kortste afstand van toren1 tot elke onverwerkte buur toe te voegen aan $P$.
- Blijf stap 2 herhalen totdat er een buur bereikt wordt die gelijk is aan toren2 (bedenk zelf hoe je dan aan de afstand komt tot toren1) of totdat $U$ leeg is (wat aangeeft dat toren2 niet kon bereikt worden vanuit toren1).
Unicode bestanden
Unicode is een internationale standaard voor de codering van binaire codes naar grafische tekens en symbolen, vergelijkbaar met de ASCII-standaard. De Unicode tekenset is echter veel uitgebreider dan de 256 symbolen van de ASCII-tekenset. Unicode ondersteunt een aantal mogelijke coderingen voor de tekenset, die aangeven hoe de symbolen binair voorgesteld worden. Als je in Python een Unicode bestand wilt openen, dan kan de gebruikte codering doorgegeven worden aan de parameter encoding van de ingebouwde functie open. Om bijvoorbeeld informatie te lezen uit het Unicode bestand chappe.txt dat gebruikt maakt van UTF-8 codering, kan het bestand als volgt geopend worden:
>>> open('chappe.txt', 'r', encoding='utf-8')
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat het bestand chappe.txt zich in de huidige directory bevindt. Dit bestand bevat een omschrijving van het netwerk van torens dat hieronder grafisch wordt weergegeven. Merk hierbij op dat er bijvoorbeeld geen verbinding is tussen Avignon en Marseille, waardoor er geen berichten kunnen verstuurd worden tussen Lille en Marseille (ze behoren tot twee verschillende subnetwerken).
>>> chappe = netwerk('chappe.txt') >>> chappe['Lille'] {'Paris', 'Bruxelles', 'Dunkerque', 'Boulogne'} >>> chappe['Paris'] {'Tours', 'Dreux', 'Tonerre', 'Lille'} >>> chappe['Brest'] {'St Brieux'} >>> tussenstations('Lille', 'Lille', chappe) 0 >>> tussenstations('Lille', 'Tours', chappe) 2 >>> tussenstations('Lille', 'Toulouse', chappe) 11 >>> tussenstations('Lille', 'Montpellier', chappe) 9 >>> tussenstations('Lille', 'Perpignan', chappe) 11 >>> tussenstations('Lille', 'Marseille', chappe) -1 >>> tussenstations('Lille', 'Londres', chappe) Traceback (most recent call last): AssertionError: stad behoort niet tot netwerk
| Added by: | Peter Dawyndt |
| Date: | 2014-06-07 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS