PROG0459 - Hidato
Forget about sudoku puzzles. The latest craze in logic puzzles is hidato. Today hidato is featured in over 60 newspapers around the world. At any moment, thousands of people play hidato online. Hidato's slogan "Find the Path… Solve the Puzzle!" is now well-known among scores of puzzle-solvers and it will probably bring fun and teach logic skills to many more in the near future. The term hidato originates from the Hebrew word for riddle (Hida, חידאתו) and is the name of a logic puzzle game invented by Dr. Gyora Benedek, an Israeli computer scientist, inventor and adventurer.
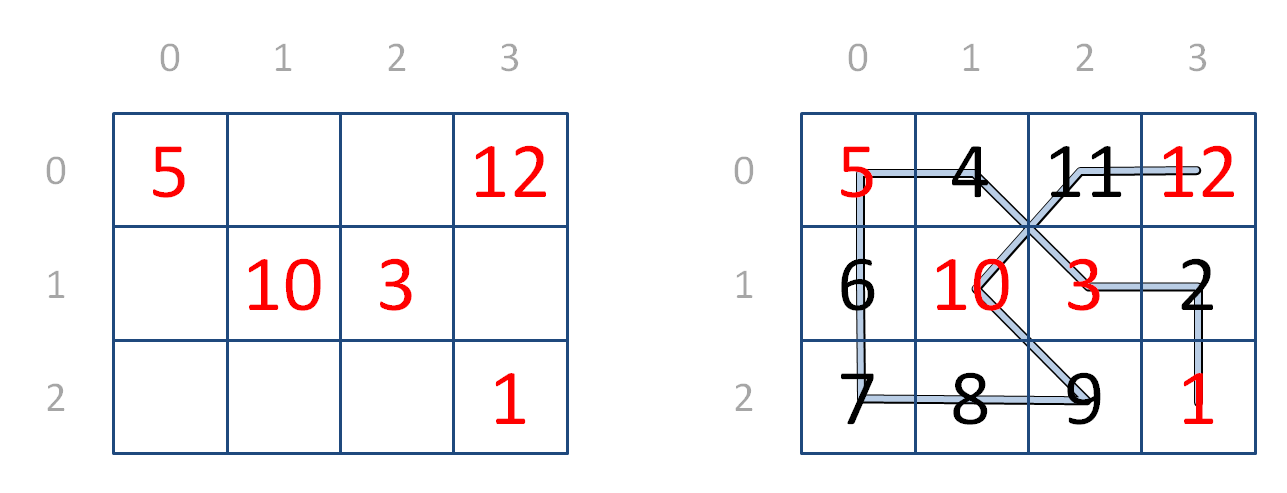
A hidato consists of a rectangular grid with $m$ rows and $n$ columns. The goal is to fill the grid with the series of consecutive numbers 1 to $m \times n$ adjacent to each other vertically, horizontally, or diagonally. In every hidato the positions of the numbers 1 and $m \times n$ on the grid are given. There are also other given numbers on the grid (with values between 1 and $m \times n$) to help direct the player how to start the solution and to ensure the hidato has a unique solution.
Assignment
In this assignment, we represent a $m \times n$ grid containing the solution of a hidato as a list containing $m$ elements. These elements represent the rows of the grid. Each row is itself a list containing $n$ integers. These represent the numbers which are filled in the successive columns of the row. You may assume that each of the numbers 1, 2, …, $m \times n$ occurs just once in the grid. The rows of the grid are indexed from top to bottom, and the columns from left to right. Indexing of the rows and columns always starts from 0. Your task is to determine whether a given $m \times n$ grid represents a valid solution of a hidato. In order to do so, you proceed as follows:
- Write a function first that takes the solution of a hidato as its argument. The function must return a tuple (r, c) that contains the row index r and the column index c of the cell in the grid that contains the value 1.
- Write a function successor that takes three arguments. The first argument is the solution of a hidato. The second and third arguments respectively represent the row and column index of a cell in the grid. The function must return a tuple (r, c) that contains the row index r and the column index c of the cell in the grid that follows upon the given cell. If the given cell contains the integer $v$, its successor is the vertically, horizontally, or diagonally adjacent cell that contains the value $v + 1$. If the given cell has no successor, the function should return the tuple (None, None).
- Use the functions first and successor to write a function last that takes the solution of a hidato as its argument. The function must return a tuple (r, c) that contains the row index r and the column index c of the cell in the grid that is found by starting from the cell containing the value 1, and repetitively visiting the next cell until a cell is reached that has no successor. The coordinates of the last visited cell must be return by the function.
- Use the function last to write a function hidato that takes the solution of a hidato as its argument. The function must return a Boolean value that indicates whether or not the given grid is a valid solution of a hidato. This can be determined by starting from the cell containing the value 1, and repetitively visiting the next cell until a cell is reached that has no successor. In case the last visited cell contains an integer that is equal to the total number of cells in the grid, the given grid represents a valid solution of a hidato.
Example
>>> first([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]]) (2, 3) >>> first([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]]) (1, 1) >>> first(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10))) (1, 1) >>> successor([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]], 2, 3) (1, 3) >>> successor([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]], 1, 3) (1, 2) >>> successor([[5, 4, 11, 2], [6, 10, 3, 12], [7, 8, 9, 1]], 2, 3) (None, None) >>> last([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]]) (0, 3) >>> last([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]]) (3, 2) >>> last(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10))) (0, 2) >>> hidato([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]]) True >>> hidato([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]]) False >>> hidato(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10))) True
Fun Fact
When asked by The New York Times where he got the idea for hidato, Dr. Benedek gave the following anwser
During SCUBA diving, I noticed a school of fish swimming at amazing speed around me. They were so fast that I could only see them at the spots where they changed direction. In my mind I worked hard to reconstruct their path. I was so fascinated that I hadn't noticed the time and the level of oxygen in my tank. Luckily, my partner signaled — time to surface. I was reluctant to leave behind this amazing dance of fish and it was still in my mind when I noticed a crumpled and wet newspaper in the shower. The only dry spot in the paper was a Sudoku puzzle. And then an idea popped in my mind: How about a printed puzzle where you reconstruct the path of the fish from observed spots? I couldn't wait to get home and start building the puzzle. A couple of weeks later, I knew I had something big. This is how Hidato was born.
Vergeet sudoku's. De nieuwste rage op het gebied van logische puzzels is de hidato. Meer dan 60 kranten wereldwijd hebben hun sudokupuzzels reeds vervangen door hidato's en het aantal online hidato-spelers groeit zienderogen. De term hidato is afgeleid van het Hebreeuwse woord voor raadsel (hida, חידאתו) en is de naam van een puzzel uitgevonden door Gyora Benedek, een Israëlische informaticus, uitvinder en avonturier.
De opgave van een hidato bestaat uit een rechthoekig rooster met $m$ rijen en $n$ kolommen. De oplossing bestaat erin de reeks natuurlijke getallen van 1 tot en met $m \times n$ in het rooster in te vullen, zodat opeenvolgende getallen horizontaal, verticaal of diagonaal naast elkaar staan. De opgave van de puzzel bevat reeds de posities van de getallen 1 en $m \times n$. Daarnaast worden in het gegeven rooster ook al een aantal andere getallen ingevuld, om de speler op weg te helpen bij het vinden van de oplossing en om te verzekeren dat de hidato een unieke oplossing heeft.
Opgave
In deze opgave stellen we een $m \times n$ rooster met de oplossing van een hidato voor als lijst met $m$ elementen. Deze elementen stellen de rijen van het rooster voor. Elke rij is zelf ook een lijst met $n$ natuurlijke getallen. Deze stellen de getallen voor die ingevuld zijn op de opeenvolgende kolomen van de rij. Je mag ervan uitgaan dat elk van de getallen 1, 2, …, $m \times n$ juist één keer voorkomt in het rooster. De rijen van het rooster worden van boven naar onder genummerd, en de kolommen van links naar rechts. Het nummeren van de rijen en de kolommen start vanaf 0. Gevraagd wordt om te bepalen of een gegeven $m \times n$ rooster een geldige oplossing van een hidato voorstelt. Hiervoor ga je als volgt te werk:
- Schrijf een functie eerste waaraan de oplossing van een hidato moet doorgegeven worden. De functie moet een tuple (r, k) teruggeven dat het rijnummer $r$ en het kolomnummer $k$ bevat van de cel in het rooster die de waarde 1 bevat.
- Schrijf een functie opvolger waaraan drie argumenten moeten doorgegeven worden. Het eerste argument is de oplossing van een hidato. Het tweede en derde argument stellen respectievelijk het rij- en kolomnummer van een cel in het rooster voor. De functie moet een tuple (r, k) teruggeven dat het rijnummer $r$ en het kolomnummer $k$ bevat van de cel in het rooster dat volgt op de gegeven cel. Als de gegeven cel het natuurlijke getal $v$ bevat, dan is de opvolger de cel die horizontaal, verticaal of diagonaal raakt aan de gegeven cel en de waarde $v + 1$ bevat. Indien de gegeven cel geen opvolger heeft, dan moet de functie het tuple (None, None) teruggeven.
- Gebruik de functies eerste en opvolger om een functie laatste te schrijven waaraan de oplossing van een hidato moet doorgegeven worden. De functie moet een tuple (r, k) teruggeven dat het rijnummer $r$ en het kolomnummer $k$ bevat van de cel in het rooster die bekomen wordt door te vertrekken vanaf de cel die de waarde 1 bevat, en telkens de volgende cel te bepalen totdat een cel bereikt wordt die geen opvolger meer heeft. De coördinaten van deze laatste cel moeten door de functie teruggegeven worden.
- Gebruik de functie laatste om een functie hidato te schrijven waaraan de oplossing van een hidato moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven, die aangeeft of het gegeven rooster een geldige oplossing van een hidato voorstelt. Dit kan bepaald worden door te vertrekken vanaf de cel die de waarde 1 bevat, en telkens de volgende cel te bepalen totdat een cel bereikt wordt die geen opvolger meer heeft. Indien deze laatste cel een getal bevat dat gelijk is aan het aantal cellen van het rooster, dan stelt het gegeven rooster een geldige oplossing van een hidato voor.
Voorbeeld
>>> eerste([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]]) (2, 3) >>> eerste([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]]) (1, 1) >>> eerste(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10))) (1, 1) >>> opvolger([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]], 2, 3) (1, 3) >>> opvolger([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]], 1, 3) (1, 2) >>> opvolger([[5, 4, 11, 2], [6, 10, 3, 12], [7, 8, 9, 1]], 2, 3) (None, None) >>> laatste([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]]) (0, 3) >>> laatste([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]]) (3, 2) >>> laatste(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10))) (0, 2) >>> hidato([[5, 4, 11, 12], [6, 10, 3, 2], [7, 8, 9, 1]]) True >>> hidato([[8, 14, 13, 12], [15, 1, 2, 11], [5, 3, 10, 16], [4, 6, 7, 9]]) False >>> hidato(((18, 19, 20, 4, 5), (17, 1, 3, 6, 8), (16, 13, 2, 9, 7), (14, 15, 12, 11, 10))) True
Weetje
Dr. Benedek beschreef als volgt aan The New York Times hoe hij aan het idee van de hidato kwam:
During SCUBA diving, I noticed a school of fish swimming at amazing speed around me. They were so fast that I could only see them at the spots where they changed direction. In my mind I worked hard to reconstruct their path. I was so fascinated that I hadn't noticed the time and the level of oxygen in my tank. Luckily, my partner signaled — time to surface. I was reluctant to leave behind this amazing dance of fish and it was still in my mind when I noticed a crumpled and wet newspaper in the shower. The only dry spot in the paper was a Sudoku puzzle. And then an idea popped in my mind: How about a printed puzzle where you reconstruct the path of the fish from observed spots? I couldn't wait to get home and start building the puzzle. A couple of weeks later, I knew I had something big. This is how Hidato was born.
| Added by: | Peter Dawyndt |
| Date: | 2014-03-23 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS