PROG0421 - Van der Waals force
The method to determine the zeroes of a quadratic function ($ax^2 + bx + c = 0$) is exact and well-known ($\Delta = b^2 - 4ac, \ldots$). The calculations become more complex when determining the zeroes of a cubic or quartic function. For quintic and higher degree functions, no formula exists to calculate their zeroes. In these cases, it has even been proven that a general formula will never be found.
Let this not discourage you. Although the positions of the zeroes cannot exactly be determined, we're still able to approximate them. Further, as the accuracy of floating point number representations within computers is limited, we can iteratively calculate the zeroes until the difference between the real zeroes and the estimated zeroes becomes smaller than the accuracy of the computer.
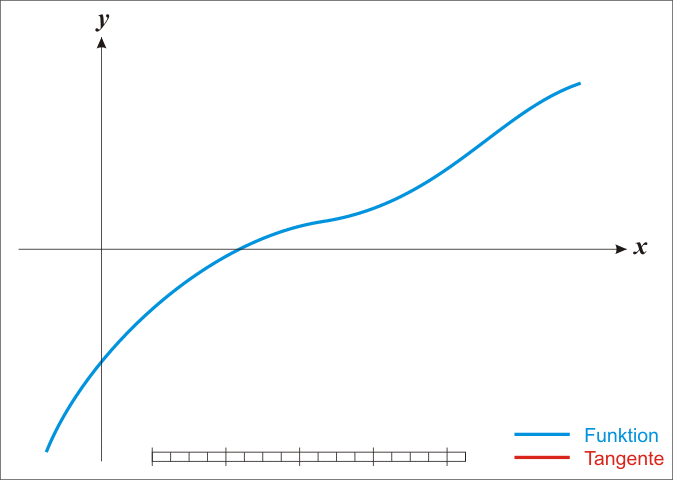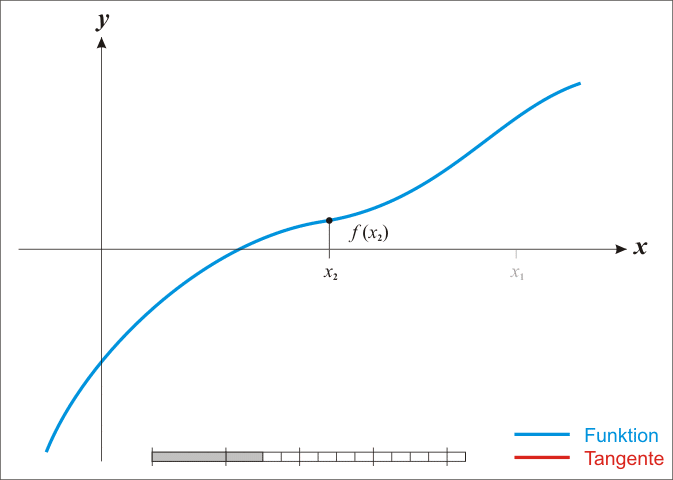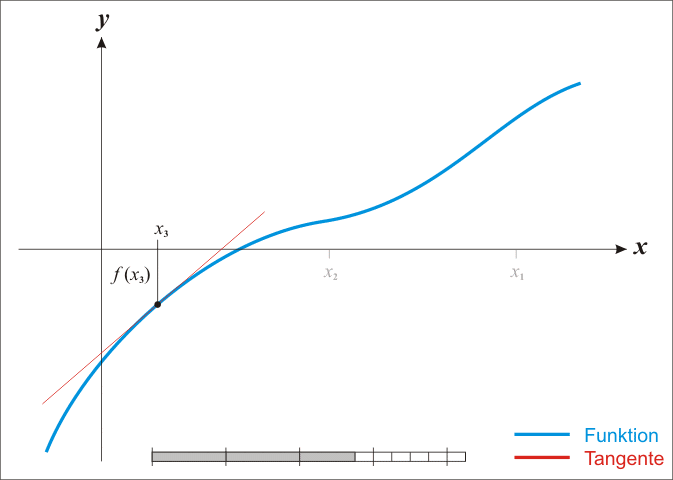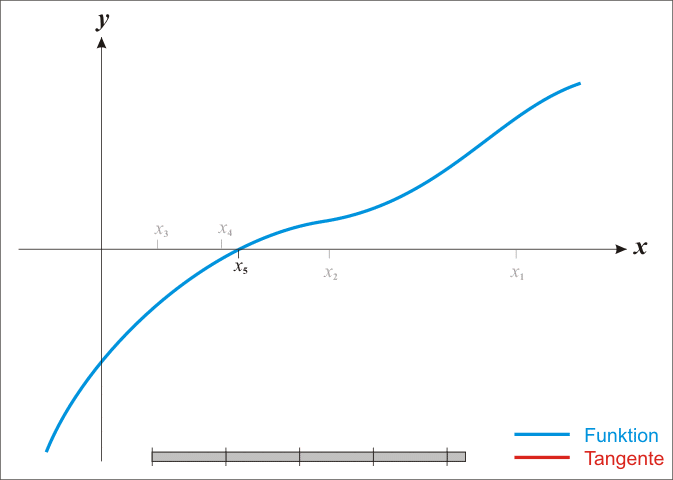
The best known method to approximate the zeroes of a function is Newton's method. This method starts with an initial approximation $x_1$ of a zero. Once an estimation $x_n$ ($n = 1, 2, \ldots$) is obtained, a new one $x_{n+1}$ that is more accurate than the previous one is calculated by determining the intersection of the tangent to the function at the point $x_n$ with the $X$ axis. This procedure is repeated, until a sufficiently accurate approximation is obtained.
In case an estimation $x_n$ of a zero is known, the next estimation may be determined as $x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$. Here, $f'$ is the derivative of the function $f$, so that $f'(x)$ denotes the slope of the tangent to the function $f$ in the point $x$. To find a good approximation of a zero using Newton's method, it is important to have an initial estimate $x_1$ that is positioned close enough to the zero (how close depends on the function itself). The series of estimates should continue until $f(x_m)$ is close enough to zero.
Exercise
The Van der Waals force $E$ between two atoms in an inert gas can be written in function of the distance $r$ between the atoms $$E(r) = \frac{A}{r^{12}} - \frac{B}{r^6}$$ in which $A$ and $B$ represent two gas constants that need to be determined experimentally. For this exercise, apply Newton's method to find the distance between two atoms where $E = 100$. In other words, search the zero of the function $f(r) = E(r) - 100$. The derivative of this function is: $$f'(r) = -\frac{12 A}{r^{13}} + \frac{6 B}{r^7}$$
Input
The input consists of three real numbers, each on a separate line. The first two lines represent the experimentally determined gas constants $A$ and $B$. De third line contains an initial estimation $r_1$ of the distance with $E(r_1) \approx 100$.
Output
Example
Input:
1.5 7.12 0.5
Output:
0.6718209666720478
Iedereen kent de methode om de nulpunten van een tweedegraadsvergelijking ($ax^2 + bx + c = 0$) exact te bepalen ($\Delta = b^2 - 4 a c, \ldots$). De berekeningen worden al een stuk ingewikkelder als men de nulpunten wil bepalen van een derde- of vierdegraadsvergelijking. Voor vergelijkingen van graad vijf of hoger bestaan er echter geen formules om de nulpunten exact te bepalen. Voor dergelijke gevallen kan zelfs bewezen worden dat er geen algemene formules bestaan.
Laat je echter niet ontmoedigen omdat de wiskundig hier tekort schiet. Als de positie van de nulpunten niet exact kan bepaald worden, dan kunnen we nog altijd proberen om de positie te benaderen. Meer nog, door de beperkte nauwkeurigheid waarmee floating point getallen in een computer opgeslagen worden, is het mogelijk om nulpunten zo nauwkeurig te benaderen dat het verschil met de exacte positie kleiner wordt dan de nauwkeurigheid van de computer.
De bekendste methode om nulpunten te benaderen is de methode van Newton. Deze methode start met een initiële benadering $x_1$ van een nulpunt. Eenmaal een benadering $x_n$ ($n = 1, 2, \ldots$) gevonden is, kan men een nieuwe benadering $x_{n+1}$ bekomen die nauwkeuriger is dan de vorige door het snijpunt te bepalen van de raaklijn aan de functie in het punt $x_n$ met de $X$-as. Deze procedure kan men blijven herhalen, totdat uiteindelijk een benadering bekomen wordt die voldoende nauwkeurig is.
Indien een benadering $x_n$ gekend is, dan kan de volgende benadering bepaald worden als $x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$. Hierbij stelt $f'$ de afgeleide van de functie $f$ voor, zodat $f'(x)$ de richtingscoëfficiënt oplevert van de raaklijn aan de functie $f$ in het punt $x$. Om een goede benadering te kunnen vinden aan de hand van de methode van Newton, is het van belang om een initiële schatting $x_1$ te hebben die voldoende dicht bij het nulpunt gelegen is (hoe dicht hangt af van de functie zelf). De reeks benaderingen kan dan voortgezet worden totdat $f(x_m)$ voldoende dicht bij nul ligt.
Opgave
De Vanderwaalskracht $E$ tussen twee atomen in een inert gas kan geschreven worden in functie van de afstand $r$ van de atomen $$E(r) = \frac{A}{r^{12}} - \frac{B}{r^6}$$ waarbij $A$ en $B$ twee gasconstanten zijn die experimenteel moeten bepaald worden. Voor deze opgave moet je de methode van Newton toepassen om de afstand tussen twee atomen te vinden waarbij $E = 100$. Je moet met andere woorden een nulpunt zoeken van de functie $f(r) = E(r) - 100$. We geven nog de afgeleide van deze functie mee: $$f'(r) = -\frac{12 A}{r^{13}} + \frac{6 B}{r^7}$$
Invoer
De invoer bestaat uit drie reële getallen, elk op een afzonderlijke regel. De eerste twee regels bevatten de experimenteel bepaalde waarden van de gasconstanten $A$ en $B$. De derde regel bevat een initiële benadering $r_1$ van een afstand waarvoor $E(r_1) \approx 100$.
Uitvoer
Voorbeeld
Invoer:
1.5 7.12 0.5
Uitvoer:
0.6718209666720478
| Added by: | Peter Dawyndt |
| Date: | 2013-09-11 |
| Time limit: | 20s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS