PROG0399 - Classification of triangles
A triangle is a geometrical shape that is formed when 3 non-collinear points are joined. The joining line segments are the sides of the triangle. The angles in between the sides on the inside of the triangle are the internal angles.
Triangles can be classified according to the length of their sides:
- Equilateral triangle: all sides are equal
- Isosceles triangle: at least 2 sides are equal in length
- Scalene triangle: all sides are unequal
Triangles can also be classified according to their internal angles:
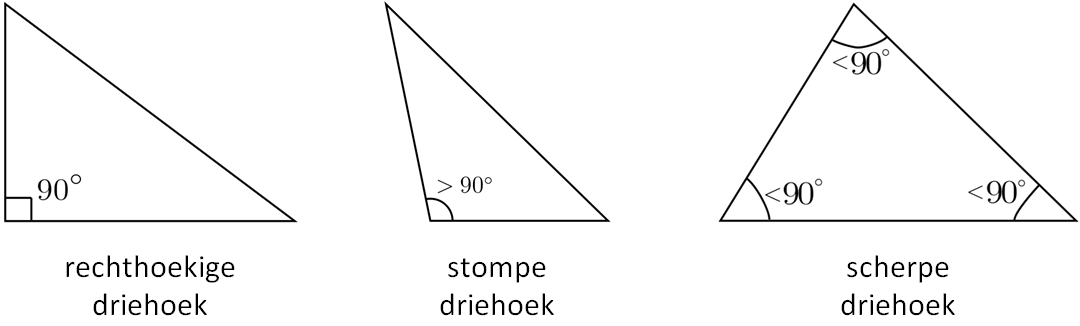
- Acute triangle: all interior angles measuring less than 90°
- Right triangle: one of its interior angles measures 90°
- Obtuse triangle: one interior angle measuring more than 90°
Length of sides between two points
The length $l$ of a side that joins the internal angles $(x_1, y_1)$ and $(x_2, y_2)$ , can be calculated as $$ l = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
Internal angle formed by 2 sides
The size of an internal angle $\gamma$ formed by two sides of a triangle can be calculated using the law of cosines $$cos(\gamma) = \frac{a^2+b^2-c^2}{2ab}$. $ , $a$ and $b$ represent the length of the sides that form the internal angle $\gamma$ , $c$ represents the length of the side right across the internal angle $\gamma$ .
Comparing floating point
numbers
For this assignment you have to compare the length of the sides with the size of the angles. Take into consideration that these figures are represented by floating point numbers. When inserted in a computer memory, minor mistakes in rounding off may occur. It is possible that a variable angle representing a 90° angle, has an actual value of 90.00000001. Therefore, testing an angle as follows is a bad idea:
if angle == 90: print('right angle')
Instead, the condition can be reformulated by stating that the size of the corner has to be "in a close range" from 90°. In the code fragment below, an angle may not deviate from 90° by more than 0.000001:
if abs(angle - 90) < 1e-6: print('right angle')
Watch this video containing further explanation about working with floating point numbers.
Assignment
Determine the name of the triangle formed by three non-collinear points, based both on its sides as well as on its internal angles.
Input
Six real numbers, each on a separate line. Every pair of consecutive numbers represents the $(x, y)$ co-ordinate for an internal angle of a triangle. You may presume that these internal angles are non-collinear.
Output
The name of the triangle that is formed by three points of which the co-ordinates are stated in the input. Use the template Triangle classification: classification_sides classification_angles. Here classification_sides is the term that represents a triangle classified according to the length of its sides. classification_angles is the term that represents a triangle classified according to the size of its internal angles. Always give the most specific term that applies to the triangle.
Example
Input:
-5.018651714882998 5.273815977515895 -4.1327268984230505 5.7376448463677665 -4.596555767274922 6.623569662827715
Output:
Triangle classification: isosceles right
Een driehoek is een meetkundige figuur die ontstaat door drie punten die niet op een rechte lijn liggen met elkaar te verbinden. De verbindende lijnstukken worden de zijden van de driehoek genoemd. De hoeken tussen de zijden aan de binnenkant van een driehoek worden de binnenhoeken van de driehoek genoemd.
Driehoeken kunnen ingedeeld worden op basis van de lengtes van hun zijden:
- gelijkzijdige driehoek: alle zijden zijn even lang
- gelijkbenige driehoek: minstens twee zijden zijn even lang
- ongelijkzijdige driehoek: alle zijden hebben een verschillende lengte
Driehoeken kunnen ook ingedeeld worden op basis van hun binnenhoeken:
- scherpe driehoek: alle hoeken zijn kleiner dan 90°
- rechthoekige driehoek: één van de hoeken is gelijk aan 90°
- stompe driehoek: één van de hoeken is groter dan 90°
Lengte van zijde tussen twee punten
De lengte $l$ van een zijde die de hoekpunten $(x_1, y_1)$ en $(x_2, y_2)$ verbindt, kan berekend worden als $$ l = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
Binnenhoek gevormd door twee zijden
De grootte van de binnenhoek $\gamma$ gevormd door twee zijden van een driehoek kan berekend worden op basis van de cosinusregel $$cos(\gamma) = \frac{a^2+b^2-c^2}{2ab}$$ Hierbij zijn $a$ en $b$ de lengten van de zijden die de binnenhoek $\gamma$ vormen, en is $c$ de lengte van de zijde die tegenover de binnenhoek $\gamma$ staat.
Vergelijken van floating point
getallen
Bij deze opgave moet je de lengte van zijden en de grootte van hoeken vergelijken. Let daarbij op het feit dat deze waarden voorgesteld worden als floating point getallen, waarbij kleine afrondingsfouten optreden als ze voorgesteld worden in een computergeheugen. Het kan dus voorvallen dat een variabele hoek die een hoek van 90° voorstelt, eigenlijk als waarde 90.00000001 heeft. Daardoor is het geen goed idee om op de volgende manier te testen of dit een rechte hoek voorstelt:
if hoek == 90: print('rechte hoek')
In plaats daarvan kan de voorwaarde geherformuleerd worden door te stellen dat de grootte van de hoek "dicht genoeg" bij 90° moet liggen. In het volgende codefragment stellen we bijvoorbeeld dat de hoek niet meer dan 0.000001 mag afwijken van 90°:
if abs(hoek - 90) < 1e-6: print('rechte hoek')
Bekijk deze video waarin extra uitleg wordt gegeven bij het werken met floating point getallen.
Opgave
Bepaal de indeling van de driehoek die gevormd wordt door drie gegeven punten die niet op een rechte lijn liggen, zowel op basis van de zijden als op basis van de binnenhoeken.
Invoer
Zes reële getallen, elk op een afzonderlijke regel. Elk paar opeenvolgende getallen stelt de $(x, y)$-coördinaat voor van een hoekpunt van een driehoek. Je mag ervan uitgaan dat deze hoekpunten niet op eenzelfde lijn liggen.
Uitvoer
Een omschrijving van de indeling van de driehoek die gevormd wordt door de drie punten waarvan de coördinaten in de invoer gegeven worden. Gebruik voor de omschrijving de template Driehoek classificatie: indeling_zijden indeling_hoeken, waarbij indeling_zijden de term is die de indeling van de driehoek op basis van de zijden aangeeft en indeling_hoeken de term is die de indeling van de driehoek op basis van de hoeken aangeeft. Gebruik telkens de meest specifieke term die van toepassing is op de driehoek.
Voorbeeld
Invoer:
-5.018651714882998 5.273815977515895 -4.1327268984230505 5.7376448463677665 -4.596555767274922 6.623569662827715
Uitvoer:
Driehoek classificatie: rechthoekige driehoek
| Added by: | Peter Dawyndt |
| Date: | 2013-06-05 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |





 RSS
RSS