SPOJ.com - Problem PROG0388

PROG0388 - Star classification

no tags

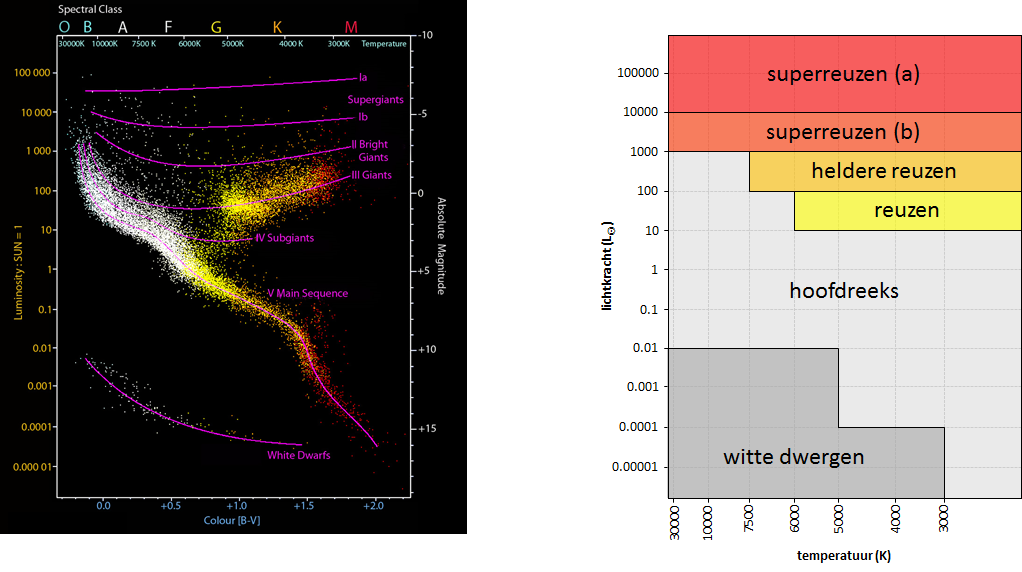
A Hertzsprung-Russell diagram is a scatter graph. The vertical axis shows the brightness of a star, expressed as absolute magnitude (magnitude corrected for distance and interstellar obscuration) or relative light intensity towards the sun. The horizontal axis shows a variable related to surface temperature, such as the B-V color index, the spectral type, or the actual temperature. Note: the temperature increases from right to left. The diagram is the usual base for the classification of stars and is used to describe their evolution. It was named after Ejnar Hertzsprung and Henry Norris Russell who introduced it independently around 1910.

Example of a Hertzsprung-Russell diagram (left) and a simple distinction of areas within the diagram that correspond to the various classes of stars (right).

Based on the position of the stars within a Hertzsprung-Russell diagram, the following classes are distinguished: supergiants (a), supergiants (b), bright giants, giants, the main sequence and white dwarfs. There is no univocal distinguishing of the areas within the diagram that correspond with the classes. For this assignment, we will take the picture on the right as a starting point. De borders of every area are parallel with one of the axis of the diagram and always correspond with one of the figures on the axis.

Assignment

Write a function classification to which two floating point numbers must be passed that respectively represent the temperature (in Kelvin) and the luminosity (relative to the sun) of a star. The function should return a string that indicates the class of the star, according to the classification in the above figure on the right. You may assume that the values of the temperature and the luminosity are alwayrs within the limits of the image, and that they will never form a point that is situated on a border of the areas used for dividing.
Write a function catalogue to which the location of a text file must be passed. The file describes a number of stars. The firs line contains a header. The following lines each contain information about one single star in fields that are separates by one tab: i) name) , ii) stellar classification, iii) temperature (in Kelvin), iv) luminosity, v) mass and vi) radius. The last three information fields are each time expressed relative to the sun. The function must return a dictionary, that displays the name of each star on a tuple that contains the floating point values of the temperature and luminosity of the star.
Write a function classes to which a dictionary must be passed that is built like the dictionaries returned by the function catalogue. The function should return a new dictionary, that displays the name of a class of stars on the collection of names of stars from the given dictionary that belong to this class. The name of a class of stars can only be used as a key in this new dictionary, if the given dictionary also contains stars that belong to this class.

Example

In the following example session we assume that the text file stars.txt is in the current directory.

>>> classification(8525.0, 196000.0) # Deneb
'supergiants (a)'
>>> classification(18890.0, 3300.0)  # Sigma Sagittarii
'supergiants (b)'
>>> classification(4925.0, 132.0)    # Zeta Hydrae
'bright giants'
>>> classification(4810.0, 45.0)     # Delta Arietis
'giants'
>>> classification(13397.0, 148.0)   # Zeta Draconis
'main sequence'
>>> classification(7740.0, 0.00049)  # Procyon A
'white dwarfs'

>>> stars = catalogue('stars.txt')
>>> stars
{'Beta Herculis': (4887.0, 151.0), 'Omicron Ursae Majoris': (5242.0, 138.0), 'Alpha Columbae': (12963.0, 1000.0), 'Beta Ursae Minoris': (4030.0, 390.0), 'Zeta Aquilae': (9620.0, 39.4), 'Epsilon Sagittarii': (5807.0, 0.89), 'Nu Ophiuchi': (4928.0, 123.0), 'Pi Orionis': (6516.0, 2.822), 'Beta Lyrae': (13300.0, 6.5), 'Beta Ceti': (4797.0, 139.1)}

>>> classes(stars)
{'main sequence': {'Pi Orionis', 'Alpha Columbae', 'Epsilon Sagittarii', 'Zeta Aquilae', 'Beta Lyrae'}, 'bright giants': {'Beta Herculis', 'Omicron Ursae Majoris', 'Nu Ophiuchi', 'Beta Ceti', 'Beta Ursae Minoris'}}

Een Hertzsprung-Russelldiagram is een puntenwolk. Op de verticale as staat de helderheid van een ster weergegeven, uitgedrukt als absolute magnitude (magnitude gecorrigeerd voor afstand en interstellaire extinctie) of relatieve lichtkracht ten opzichte van de zon. Op de horizontale as staat een variabele gerelateerd aan de oppervlaktetemperatuur, zoals de B-V-kleurindex, de spectraalklasse, of de effectieve temperatuur. Opgelet: de temperatuur neemt toe van rechts naar links. Het diagram is de gebruikelijke basis voor de classificatie van sterren en wordt gebruikt om hun evolutie te beschrijven. Het is genoemd naar Ejnar Hertzsprung en Henry Norris Russell die het omstreeks 1910 onafhankelijk van elkaar introduceerden.

Voorbeeld van een Hertzsprung-Russelldiagram (links) en een eenvoudige afbakening van gebieden binnen het diagram die corresponderen met de verschillende klassen van sterren (rechts).

Op basis van de positie van de sterren binnen een Hertzsprung-Russelldiagram worden de volgende klassen onderscheiden: superreuzen (a), superreuzen (b), heldere reuzen, reuzen, de hoofdreeks en witte dwergen. Er bestaat geen eenduidige afbakening van de gebieden in het diagram die corresponderen met de verschillende klassen. Voor deze opgave zullen we uitgaan van de afbakening die staat weergegeven in de rechter figuur hierboven. De randen van elk gebied liggen daarbij telkens parallel met één van de assen van het diagram en vallen steeds samen met één van de waarden die op de assen staan weergegeven.

Opgave

Schrijf een functie classificatie waaraan twee floating point getallen moeten doorgegeven worden die respectievelijk de temperatuur (in Kelvin) en de lichtkracht (relatief ten opzichte van de zon) van een ster voorstellen. De functie moet een string teruggeven die aangeeft tot welke klasse de ster behoort, volgens de indeling die gemaakt wordt in de rechter figuur hierboven. Je mag ervan uitgaan dat de waarden van de temperatuur en de lichtkracht steeds binnen de grenzen van de afbeelding vallen, en dat ze nooit een punt vormen dat op de rand ligt van de gebieden die bij de indeling gebruikt worden.
Schrijf een functie cataloog waaraan de locatie van een tekstbestand moet doorgegeven worden. Het bestand omschrijft een aantal sterren. De eerste regel bevat een hoofding. De volgende regels geven telkens de volgende informatie van één enkele ster weer in velden die van elkaar gescheiden worden door één enkele tab: i) naam, ii) spectraalklasse, iii) temperatuur (in Kelvin), iv) lichtkracht, v) massa en vi) straal. De laatste drie informatievelden worden telkens uitgedrukt relatief ten opzichte van de zon. De functie moet een dictionary teruggeven, die de naam van elke ster afbeeldt op een tuple dat de floating point waarden bevat van de temperatuur en lichtkracht van de ster.
Schrijf een functie klassen waaraan een dictionary moet doorgegeven worden die is opgebouwd zoals de dictionaries die door de functie cataloog teruggegeven worden. De functie moet een nieuwe dictionary teruggeven, die de naam van een klasse van sterren afbeeldt op de verzameling namen van sterren uit de gegeven dictionary die tot die klasse behoren. De naam van een klasse van sterren mag enkel gebruikt worden als sleutel in deze nieuwe dictionary, indien de gegeven dictionary daadwerkelijk ook sterren bevat die tot deze klasse behoren.

Voorbeeld

Bij onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand sterren.txt zich in de huidige directory bevindt.

>>> classificatie(8525.0, 196000.0) # Deneb
'superreuzen (a)'
>>> classificatie(18890.0, 3300.0)  # Sigma Sagittarii
'superreuzen (b)'
>>> classificatie(4925.0, 132.0)    # Zeta Hydrae
'heldere reuzen'
>>> classificatie(4810.0, 45.0)     # Delta Arietis
'reuzen'
>>> classificatie(13397.0, 148.0)   # Zeta Draconis
'hoofdreeks'
>>> classificatie(7740.0, 0.00049)  # Procyon A
'witte dwergen'

>>> sterren = cataloog('sterren.txt')
>>> sterren
{'Beta Herculis': (4887.0, 151.0), 'Omicron Ursae Majoris': (5242.0, 138.0), 'Alpha Columbae': (12963.0, 1000.0), 'Beta Ursae Minoris': (4030.0, 390.0), 'Zeta Aquilae': (9620.0, 39.4), 'Epsilon Sagittarii': (5807.0, 0.89), 'Nu Ophiuchi': (4928.0, 123.0), 'Pi Orionis': (6516.0, 2.822), 'Beta Lyrae': (13300.0, 6.5), 'Beta Ceti': (4797.0, 139.1)}

>>> klassen(sterren)
{'hoofdreeks': {'Pi Orionis', 'Alpha Columbae', 'Epsilon Sagittarii', 'Zeta Aquilae', 'Beta Lyrae'}, 'heldere reuzen': {'Beta Herculis', 'Omicron Ursae Majoris', 'Nu Ophiuchi', 'Beta Ceti', 'Beta Ursae Minoris'}}

Submit solution!

Added by:	Peter Dawyndt
Date:	2013-06-03
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None