PROG0381 - Victoria amazonica
Victoria amazonica is a species of flowering plant, the largest of the Nymphaeaceae family of water lilies. It thrives at a temperature of 27-30 °C and is native to the shallow waters of the Amazon River basin, such as oxbow lakes and bayous. In Belgium, the plant can be admired in the botanical garden of Ghent University (Ghent) and the National Botanic Garden of Belgium (Meise).
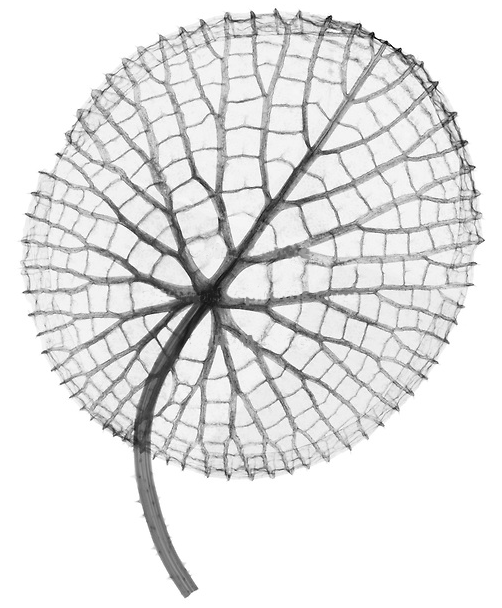
The leaves of V. amazonica are maroon when they reach the surface, but turn green later on. Young leaves have short edges that are curled inwards. Older leaves can grow up to 3 meter in diameter and float on the water's surface on a submerged stalk, 7 to 8 meter in length. The largest leaves can easily carry 40 kg. The underside of the leaves is covered with thorns and prominent ribs that form an irregular pattern of cells.
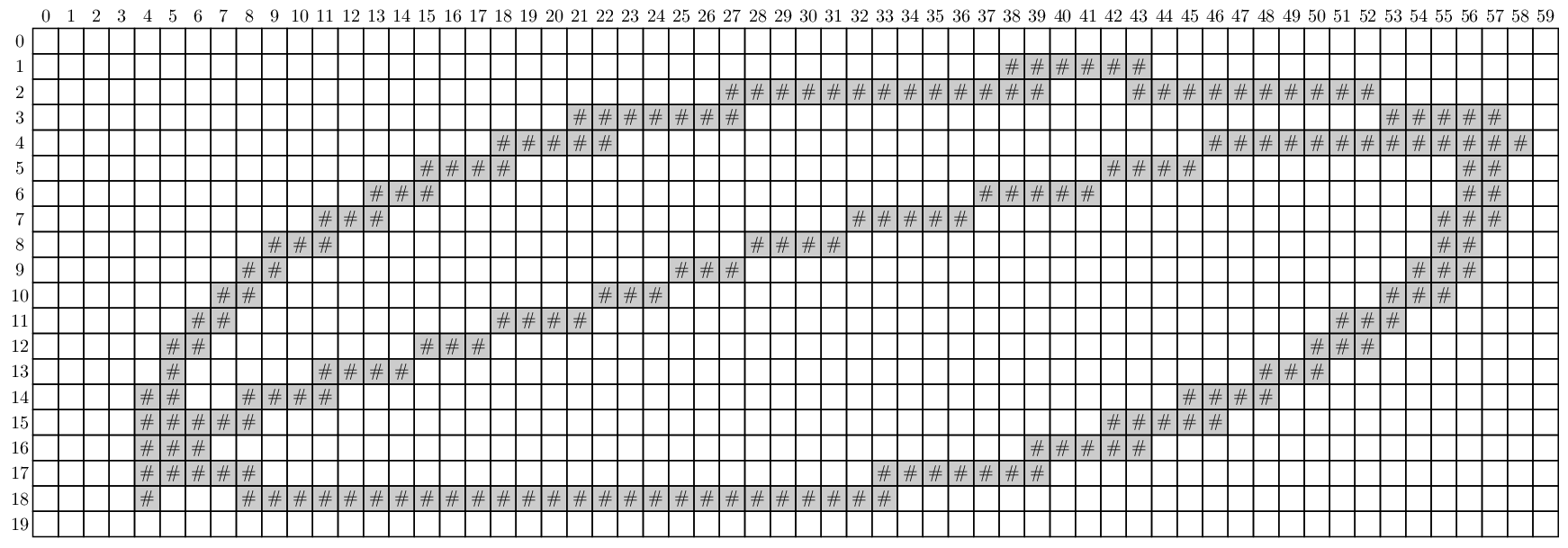
To investigate a plant species we want to count the number of cells on its leaves and determine the average size of these leaf cells. To do this, we convert images of leaves into bitmaps in which leaf cells are clearly delineated. Such a bitmap is nothing more than a rectangular grid and the squares of the bitmap are called bits. Each bit in the grid is either empty (represented by a space) or covered by a piece of rib of the leaf (represented by a pound sign: #). Below you see an example image of a simple leaf having only two cells (left) and the bitmap we have created from this image (right). In a bitmap, leaf cells correspond to regions of contiguous empty bits. Bits are called contiguous if they share a common side. A region of contiguous empty bits is never considered to be a leaf cell, if it contains empty bits on the outer border of the bitmap.
Assignment
Define a class Leaf that can be used to analyze plant leafs. The objects of this class must at least have the following methods:
- An initialization method __init__ that takes the location of a text file as an argument. This text file contains a bitmap of the leaf under analysis.
- A method __str__ that returns the string representation of the leaf. This string represents the rectangular grid as it is read from the given bitmap file. Apart from empty bits (represented by spaces) and bits that coincide with ribs of the leaf (represented by pound signs: #), bits can also be filled (represented by dots). Filling up bits happens when the fill method is called (see below).
- A method fill that takes the row and column index of an empty cell in the bitmap. The rows of a bitmap are indexed top to bottom, the columns left to right, and indexing starts at zero in both cases. If the bit at the given position is not empty, the method must throw an AssertionError with the message bit must be empty. Otherwise, all bits of the region of contiguous empty bits that contains the given empty bit must be marked as filled (they thus are not longer considered empty after the method has been called), and the method must return the number of bits contained in this region.
- A method clear that marks all filled bits as empty. Note that the filled bits in the bitmap may belong to multiple leaf cells, for example if the method fill is called multiple times before the method clear is called.
- Use the methods fill and clear to write a method cells that returns the number of leaf cells whose size is not smaller than the given minimal cell size. The minimal size of a leaf cell can be passed to the optional parameter minimum (default value: 1). The size of a leaf cell is expressed as the number of bits contained in the corresponding region of contiguous empty bits in the bitmap. Taking into account a minimal cell size is important to exclude small artifacts that might pop up while converting the image of the leaf into its corresponding bitmap. Note again that regions of contiguous empty bits that contain empty bits on the outer border are never considered as leaf cells. These regions must be ignored when the method counts the leaf cells. Make sure that the bitmap has no filled bits after calling this method.
- Use the methods fill and clear to write a method cellsize that returns the average cell size of all leaf cells whose size is not smaller than the given minimal cell size. The minimal size of a leaf cell can be passed to the optional parameter minimum (default value: 1). As with the previous method, this method should also not consider regions of contiguous empty bits that contain empty bits on the outer border of the bitmap as leaf cells, and the bitmap may not contain filled bits after the method has been called. The method must return the value None if there are no leaf cells that are larger than or equal to the given minimal cell size.
Example
In the following interactive session we assume that the text files leaf.txt and victoria.txt are located in the current directory. The first file contains the bitmap created from the image of the simple leaf used as an example above. The second file contains a bitmap created from the image of the underside of a leaf of V. amazonica that we have used in the introduction of this assignment.
>>> leaf = Leaf('leaf.txt') >>> print(leaf) <BLANKLINE> ###### ############# ########## ####### ##### ##### ############# #### #### ## ### ##### ## ### ##### ### ### #### ## ## ### ### ## ### ### ## #### ### ## ### ### # #### ### ## #### #### ##### ##### ### ##### ##### ####### # ########################## <BLANKLINE> >>> leaf.fill(5, 30) 182 >>> print(leaf) <BLANKLINE> ###### #############...########## #######.........................##### #####.......................############# ####.......................#### ## ###.....................##### ## ###..................##### ### ###................#### ## ##...............### ### ##.............### ### ##..........#### ### ##........### ### #.....#### ### ##..#### #### ##### ##### ### ##### ##### ####### # ########################## <BLANKLINE> >>> leaf.fill(8, 30) Traceback (most recent call last): AssertionError: bit must be empty >>> leaf.fill(15, 30) 335 >>> print(leaf) <BLANKLINE> ###### #############...########## #######.........................##### #####.......................############# ####.......................####..........## ###.....................#####..............## ###..................#####..................### ###................####.......................## ##...............###..........................### ##.............###............................### ##..........####.............................### ##........###................................### #.....####.................................### ##..####.................................#### #####.................................##### ###................................##### #####........................####### # ########################## <BLANKLINE> >>> leaf.clear() >>> print(leaf) <BLANKLINE> ###### ############# ########## ####### ##### ##### ############# #### #### ## ### ##### ## ### ##### ### ### #### ## ## ### ### ## ### ### ## #### ### ## ### ### # #### ### ## #### #### ##### ##### ### ##### ##### ####### # ########################## <BLANKLINE> >>> leaf.cells() 2 >>> leaf.cellsize() 258.5 >>> victoria = Leaf('victoria.txt') >>> victoria.cells() 242 >>> victoria.cells(minimum=10) 219 >>> victoria.cells(minimum=20) 213 >>> victoria.cellsize() 107.86363636363636 >>> victoria.cellsize(minimum=10) 118.74885844748859 >>> victoria.cellsize(minimum=20) 121.64319248826291
Victoria amazonica is de grootste waterlelie ter wereld. Deze soort heeft een temperatuur van 27-30 °C nodig, wat zelfs in de tropen niet overal voorkomt. Ze komt van nature voor in stilstaand of langzaam stromend water in Brazilië, Colombia, Guyana en Peru. In België kan de plant bewonderd worden in de plantentuin van de Universiteit Gent (Gent) en de Nationale Plantentuin van België (Meise).
De bladeren van V. amazonica zijn kastanjebruin als ze het wateroppervlak bereiken, maar worden later groen. Jonge bladeren hebben korte, naar binnen omgekrulde randen. Oudere bladeren kunnen een diameter tot 3 meter bereiken. Ze hebben een 4–10 cm hoge rand en drijven aan 7 tot 8 meter lange stengels. De grootste bladeren hebben een draagvermogen van 40 kg. De bladeren zijn aan de onderkant bezet met stekels en opvallende ribben die een onregelmatig patroon van cellen vormen.
Om een plantensoort te onderzoeken willen we het aantal cellen aan de onderkant van zijn bladeren tellen en de gemiddelde grootte van een bladcel bepalen. Hiervoor zetten we telkens een afbeelding van een blad om in een bitmap waarin de bladcellen duidelijk afgelijnd zijn. Zo een bitmap is niets anders dan een rechthoekig rooster en de vakjes van dit rooster worden bits genoemd. Elke bit van het rooster is leeg (voorgesteld door een spatie) of wordt bedekt door een stuk rib van het blad (voorgesteld door een hekje: #). Als voorbeeld zie je hieronder een afbeelding van een eenvoudig blad met twee cellen (links) en de bitmap die we van deze afbeelding gemaakt hebben (rechts). In een bitmap wordt een bladcel gevormd door een gebied van aangrenzende lege bits. Bits worden hierbij aangrenzend genoemd als ze een gemeenschappelijke zijde hebben. Een gebied van aangrenzende lege bits wordt nooit als een bladcel beschouwt als het bits op de buitenste rand van de bitmap bevat.
Opgave
Definieer een klasse Blad waarmee bladeren van planten kunnen geanalyseerd worden. De objecten van deze klasse moeten minstens de volgende methoden hebben:
- Een initialisatiemethode __init__ waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit tekstbestand bevat een bitmap van het blad dat moet geanalyseerd worden.
- Een methode __str__ die een stringvoorstelling van het blad teruggeeft. Deze stringvoorstelling geeft het rechthoekig rooster weer zoals het uit het opgegeven bitmapbestand werd gelezen. Naast lege bits (voorgesteld door spaties) en bits die samenvallen met ribben van het blad (voorgesteld door hekjes: #), kunnen bits daarnaast ook opgevuld zijn (voorgesteld door punten). Dit opvullen gebeurt door het aanroepen van de methode opvullen (zie verder).
- Een methode opvullen waaraan het rij- en kolomnummer van een lege bit in de bitmap moet doorgegeven worden. De rijen van een bitmap worden genummerd van boven naar onder, de kolommen van links naar rechts, en de nummering start telkens vanaf nul. Indien de bit op de opgegeven positie niet leeg is, moet de methode een AssertionError opwerpen met de tekst bit moet leeg zijn. Anders moeten alle bits van het gebied van aangrenzend lege bits waartoe de opgegeven bit behoort als opgevuld gemarkeerd worden (ze worden dus niet langer als leeg beschouwd nadat de methode werd aangeroepen) en moet de methode teruggeven uit hoeveel bits dit gebied bestaat.
- Een methode wissen die alle opgevulde bits van de bitmap terug als leeg markeert. Merk op dat de opgevulde bits in de bitmap mogelijks tot meerdere cellen kunnen behoren, bijvoorbeeld als de methode opvullen verschillende keren werd aangeroepen voordat de methode wissen wordt aangeroepen.
- Gebruik de methoden opvullen en wissen om een methode cellen te schrijven die het aantal bladcellen teruggeeft die niet kleiner zijn dan de opgegeven minimale celgrootte. De minimale celgrootte kan doorgegeven worden aan de optionele parameter minimum (standaardwaarde: 1). De grootte van een bladcel wordt uitgedrukt als het aantal bits in het overeenkomstige gebied van aaneengesloten lege bits in de bitmap. Het gebruik van een minimale celgrootte is belangrijk om kleine artefacten uit te sluiten die kunnen ontstaan bij het omzetten van de afbeelding van het blad naar de overeenkomstige bitmap. We merken hier opnieuw op dat gebieden van aaneengesloten lege bits die bits op de buitenste rand van de bitmap bevatten niet als bladcel mogen beschouwd worden. Deze gebieden moeten dus genegeerd worden als de methode de bladcellen telt. Zorg ervoor dat de bitmap geen opgevulde bits heeft nadat de methode werd aangeroepen.
- Gebruik de methoden opvullen en wissen om een methode celgrootte te schrijven die de gemiddelde celgrootte teruggeeft van alle bladcellen die niet kleiner zijn dan de opgegeven minimale celgrootte. De minimale celgrootte kan doorgegeven worden aan de optionele parameter minimum (standaardwaarde: 1). Net zoals de vorige methode mag ook deze methode de gebieden van aaneengesloten lege bits die bits op de buitenste rand van de bitmap bevatten niet als bladcellen beschouwen, en mag de bitmap ook geen opgevulde bits vertonen na het aanroepen van de methode. De methode moet de waarde None teruggeven indien er geen bladcellen zijn die groter of gelijk zijn dan de opgegeven minimale celgrootte.
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat de tekstbestanden blad.txt en victoria.txt zich in de huidige directory bevinden. Het eerste bestand bevat de bitmap die gemaakt werd van de afbeelding van het eenvoudige blad dat hierboven als voorbeeld gebruikt werd. Het tweede bestand bevat een bitmap die gemaakt werd op basis van de afbeelding met de onderkant van een blad van de V. amazonica die we in de inleiding van deze opgave gebruikt hebben.
>>> blad = Blad('blad.txt') >>> print(blad) <BLANKLINE> ###### ############# ########## ####### ##### ##### ############# #### #### ## ### ##### ## ### ##### ### ### #### ## ## ### ### ## ### ### ## #### ### ## ### ### # #### ### ## #### #### ##### ##### ### ##### ##### ####### # ########################## <BLANKLINE> >>> blad.opvullen(5, 30) 182 >>> print(blad) <BLANKLINE> ###### #############...########## #######.........................##### #####.......................############# ####.......................#### ## ###.....................##### ## ###..................##### ### ###................#### ## ##...............### ### ##.............### ### ##..........#### ### ##........### ### #.....#### ### ##..#### #### ##### ##### ### ##### ##### ####### # ########################## <BLANKLINE> >>> blad.opvullen(8, 30) Traceback (most recent call last): AssertionError: bit moet leeg zijn >>> blad.opvullen(15, 30) 335 >>> print(blad) <BLANKLINE> ###### #############...########## #######.........................##### #####.......................############# ####.......................####..........## ###.....................#####..............## ###..................#####..................### ###................####.......................## ##...............###..........................### ##.............###............................### ##..........####.............................### ##........###................................### #.....####.................................### ##..####.................................#### #####.................................##### ###................................##### #####........................####### # ########################## <BLANKLINE> >>> blad.wissen() >>> print(blad) <BLANKLINE> ###### ############# ########## ####### ##### ##### ############# #### #### ## ### ##### ## ### ##### ### ### #### ## ## ### ### ## ### ### ## #### ### ## ### ### # #### ### ## #### #### ##### ##### ### ##### ##### ####### # ########################## <BLANKLINE> >>> blad.cellen() 2 >>> blad.celgrootte() 258.5 >>> victoria = Blad('victoria.txt') >>> victoria.cellen() 242 >>> victoria.cellen(minimum=10) 219 >>> victoria.cellen(minimum=20) 213 >>> victoria.celgrootte() 107.86363636363636 >>> victoria.celgrootte(minimum=10) 118.74885844748859 >>> victoria.celgrootte(minimum=20) 121.64319248826291
| Added by: | Peter Dawyndt |
| Date: | 2013-06-02 |
| Time limit: | 20s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS