PROG0378 - Error correction in reads
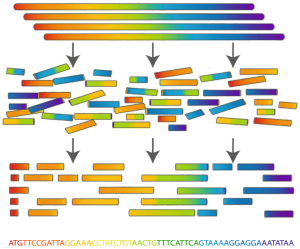
Determining an organism's complete genome (called genome sequencing) is one of the cornerstones of bioinformatics. Unfortunately, we still don't possess the microscope technology to zoom in to the nucleotide level and determine the sequence of a genome's nucleotides, one at a time. However, researchers can apply chemical methods to generate and identify much smaller snippets of DNA, called reads. After obtaining a large collection of reads from multiple copies of the same genome, the remaining challenge is to reconstruct the desired genome from these small pieces of DNA. This process is called genome assembly.
Even though genome sequencing now has become a multi-billion dollar enterprise, the sequencing machines that identify the reads still produce errors a substantial percentage of the time. To make matters worse, these errors are unpredictable. It is difficult to determine if the machine has made an error, let alone where in the read the error has occurred. For this reason, error correction in reads is typically a vital first step in genome assembly. As is the case with point mutations, the most common type of sequencing error occurs when a single nucleotide from a read is interpreted incorrectly.
Assignment
You are given a collection of reads of equal length. For each read $r$ in the data set, one of the following applies:
- $r$ was correctly sequenced and appears in the data set at least twice (possibly as a reverse complement)
- $r$ is incorrect (it appears in the data set exactly once) and its Hamming distance is 1 with respect to exactly one correct read in the data set (or the reverse complement of that read); in this case, the correct read (or its reverse complement) can be used as the error correction for the incorrect read
- $r$ is incorrect (it appears in the data set exactly once) and has Hamming distance at least 2 with respect to all correct reads and the reverse complement of all correct reads in the data set; in that case, the incorrect read is called an orphan for which no error correction can be suggested
Your task is to determine the orphan reads and to determine the error corrections for the other incorrect reads. In order to do so, you proceed as follows:
- Write a function hamming that takes two strings. The function must throw an AssertionError with the message strings should have equal length in case both strings have a different length. Otherwise, the function must return the Hamming distance between both strings.
- Write a function complement that takes a DNA sequence (this is a string that only contains the uppercase letters A, C, G and T) as an argument. The function must return the reverse complement of the given DNA sequence.
- Write a function normalform that takes a DNA sequence as an argument. The function must either return the given sequence itself, or its reverse complement, depending on which one comes first lexicographically. We call this the normal form of the DNA sequence.
- Write a function occurrences that takes a collection (a list, tuple, …) of reads as an argument. The function must return a dictionary that maps the normal form of each read in the given collection onto the number of reads with that normal form in the given collection.
- Write a function errors that takes a collection (a list, tuple, …) of reads as an argument. The function may assume that all reads have equal length. The function must return a tuple containing two elements. The first element is the set containing all orphan reads from the given collection. The second element is the lexicographically sorted list of all other incorrect reads. Each incorrect read in that list is represented as a tuple that — apart from the incorrect read itself — also contains the corrected version of the read as a second element. Sorting only depends on the incorrect reads.
Reverse complement
The reverse complement of a DNA string is formed by reversing the string and taking the complement of each base symbol (A and T are complementary base symbols, as are C and G). We must reverse the string in addition to taking complements because of the directionality of DNA. DNA replication and transcription occurs from the 5' end to the 3' end, and the 3' end of one strand is opposite from the 5' end of the complementary strand. Thus, if we were to simply take complements, then we would be reading the second strand in the wrong direction.
Hamming distance
The Hamming distance between two strings having the same length is the minimum number of symbol substitutions required to transform one string into the other. If the strings are given by $s_1$ and $s_2$, then we write the Hamming distance between them as $d_H(s_1,s_2)$.
We can compute the Hamming distance by visual inspection: the Hamming distance between two strings is simply the number of positions in the strings at which corresponding symbols differ. For example, the Hamming distance between the two strings in the figure below is equal to 7.
Example
>>> hamming('TTCAT', 'TTCAT') 0 >>> hamming('TTCAT', 'TTGAT') 1 >>> hamming('TTCAT', 'GAGGA') 5 >>> hamming('TTCAT', 'TTT') Traceback (most recent call last): AssertionError: strings should have equal length >>> complement('TTCAT') 'ATGAA' >>> complement('TTGAT') 'ATCAA' >>> complement('GAGGA') 'TCCTC' >>> normalform('TTCAT') 'ATGAA' >>> normalform('TTGAT') 'ATCAA' >>> normalform('GAGGA') 'GAGGA' >>> reads = ['TCATC', 'TTCAT', 'TCATC', 'TGAAA', 'GAGGA', 'TTTCA', 'ATCAA', 'TTGAT', 'AGGCT'] >>> occurrences(reads) {'GAGGA': 1, 'ATGAA': 1, 'TGAAA': 2, 'GATGA': 2, 'AGCCT': 1, 'ATCAA': 2} >>> errors(reads) ({'AGGCT'}, [('GAGGA', 'GATGA'), ('TTCAT', 'TTGAT')]) >>> reads = ['GATTA', 'GATTA', 'TAATC', 'GAATC', 'GATTA', 'TAAGC', 'TAATA'] >>> occurrences(reads) {'GATTA': 4, 'TAATA': 1, 'GCTTA': 1, 'GAATC': 1} >>> errors(reads) (set(), [('GAATC', 'TAATC'), ('TAAGC', 'TAATC'), ('TAATA', 'TAATC')])
Het bepalen van het volledige genoom van een organisme (genoomsequenering) is één van de hoekstenen van de bioinformatica. Helaas beschikken we nog steeds niet over microscopische technologie die toelaat om tot op nucleotideniveau in te zoomen en zo de reeks nucleotiden van een genoom één voor één af te lezen. Onderzoekers beschikken echter wel over chemische methoden die kunnen toegepast worden voor het genereren en identificeren van kortere DNA fragmenten. In deze context worden de korte fragmenten reads genoemd. Nadat we een grote collectie van reads geïdentificeerd hebben uit meerdere kopieën van hetzelfde genoom, blijft de uitdaging om het genoom te reconstrueren uit deze korte stukjes DNA. Dit proces wordt genoomassemblage genoemd.
Ondanks het feit dat genoomsequenering vandaag de dag is uitgegroeid tot een miljardenbusiness, blijven de sequeneringsmachines die de reads identificeren nog steeds in een substantieel aantal gevallen fouten produceren. Om het nog erger te maken, zijn deze fouten ook nog eens onvoorspelbaar. Het is moeilijk om te bepalen of de machine een fout gemaakt heeft, laat staan om te bepalen waar de fout voorkomt in de read. Daarom is foutcorrectie van de reads meestal een belangrijke eerste stap bij genoomassemblage. Zoals dat ook met puntmutaties het geval is, komen fouten waarbij één enkele nucleotide van de read verkeerd geïnterpreteerd wordt het vaakst voor.
Opgave
Gegeven is een collectie van reads die allemaal even lang zijn. Voor elke read $r$ in deze collectie is één van de volgende uitspraken van toepassing:
- $r$ werd correct gesequeneerd en komt minstens twee keer voor in de dataset (mogelijk als een invers complement)
- $r$ werd verkeerd gesequeneerd (de read komt slechts één keer voor in de dataset) en er is juist één correcte read (of het invers complement van die read) in de dataset waarvoor de Hammingafstand ten opzichte van de verkeerde read gelijk is aan 1; in dit geval kan de correcte read (of zijn invers complement) beschouwd worden als de foutcorrectie van de verkeerde read
- $r$ werd verkeerd gesequeneerd (de read komt slechts één keer voor in de dataset) en heeft Hammingafstand minstens 2 met alle correcte reads en het invers complement van alle correcte reads in de dataset; in dat geval wordt de verkeerde read een wees genoemd waarvoor geen foutcorrectie kan gesuggereerd worden
Je opdracht bestaat erin om de verweesde reads te bepalen en om de foutcorrecties te bepalen voor de andere verkeerde reads. Hiervoor ga je als volgt te werk:
- Schrijf een functie hamming waaraan twee strings moeten doorgegeven worden. De functie moet een AssertionError opwerpen met de boodschap strings moeten even lang zijn indien de gegeven strings niet dezelfde lengte hebben. Anders moet de functie de Hammingafstand tussen beide strings teruggeven.
- Schrijf een functie complement waaraan een DNA sequentie moet doorgegeven worden (dit is een string die enkel bestaat uit de hoofdletters A, C, G en T). De functie moet het invers complement van de gegeven DNA sequentie teruggeven.
- Schrijf een functie normaalvorm waaraan een DNA sequentie moet doorgegeven worden. De functie moet ofwel de gegeven sequentie zelf teruggeven, of diens invers complement, afhankelijk van welke string alfabetisch eerst komt. We noemen die string de normaalvorm van de DNA sequentie.
- Schrijf een functie voorkomens waaraan een collectie (een lijst, tuple, …) van reads moet doorgegeven worden. De functie moet een dictionary teruggeven die de normaalvorm van elke read uit de collectie afbeeldt op het aantal keer dat een read met die normaalvorm voorkomt in de gegeven collectie.
- Schrijf een functie fouten waaraan een collectie (een lijst, tuple, …) van reads moet doorgegeven worden. De functie mag hierbij veronderstellen dat alle reads dezelfde lengte hebben. De functie moet een tuple met twee elementen teruggeven. Het eerste element is de verzameling van verweesde reads uit de gegeven collectie. Het tweede element is de alfabetisch gesorteerde lijst van alle andere verkeerde reads. Elke verkeerde read uit die lijst wordt voorgesteld als een tuple dat — naast de verkeerde read zelf — als tweede element ook de correctie van de read bevat. Het sorteren moet enkel gebeuren op basis van de verkeerde reads.
Invers complement
Het invers complement van een DNA sequentie wordt verkregen door de string om te keren en het complement te nemen van elke base (A en T zijn complementaire basen, net zoals C en G). Naast het nemen van het complement moeten we de string ook omkeren omwille van de gerichtheid van DNA. DNA-replicatie en -transcriptie gebeuren immers van het 5' uiteinde tot het 3' uiteinde, en het 3' uiteinde van de ene streng ligt tegenover het 5' uiteinde van de complementaire streng. Als we dus gewoon het complement zouden nemen, dan zou de tweede streng in de verkeerde richting gelezen worden.
Hammingafstand
De Hammingafstand tussen twee strings met dezelfde lengte is het minimaal aantal karakters dat moet vervangen worden om de ene string om te zetten in de andere. Als de strings worden aangeduid door $s_1$ en $s_2$, dan wordt de Hammingafstand tussen beide strings genoteerd als $d_H(s_1,s_2)$.
De berekening van de Hammingafstand kan makkelijk visueel voorgesteld worden: de afstand tussen twee strings is immers niets anders dan het aantal posities waarop verschillende karakters voorkomen in beide strings. Zo is de Hammingafstand tussen de twee strings die hieronder weergegeven worden bijvoorbeeld gelijk aan 7.
Voorbeeld
>>> hamming('TTCAT', 'TTCAT') 0 >>> hamming('TTCAT', 'TTGAT') 1 >>> hamming('TTCAT', 'GAGGA') 5 >>> hamming('TTCAT', 'TTT') Traceback (most recent call last): AssertionError: strings moeten even lang zijn >>> complement('TTCAT') 'ATGAA' >>> complement('TTGAT') 'ATCAA' >>> complement('GAGGA') 'TCCTC' >>> normaalvorm('TTCAT') 'ATGAA' >>> normaalvorm('TTGAT') 'ATCAA' >>> normaalvorm('GAGGA') 'GAGGA' >>> reads = ['TCATC', 'TTCAT', 'TCATC', 'TGAAA', 'GAGGA', 'TTTCA', 'ATCAA', 'TTGAT', 'AGGCT'] >>> voorkomens(reads) {'GAGGA': 1, 'ATGAA': 1, 'TGAAA': 2, 'GATGA': 2, 'AGCCT': 1, 'ATCAA': 2} >>> fouten(reads) ({'AGGCT'}, [('GAGGA', 'GATGA'), ('TTCAT', 'TTGAT')]) >>> reads = ('GATTA', 'GATTA', 'TAATC', 'GAATC', 'GATTA', 'TAAGC', 'TAATA') >>> voorkomens(reads) {'GATTA': 4, 'TAATA': 1, 'GCTTA': 1, 'GAATC': 1} >>> fouten(reads) (set(), [('GAATC', 'TAATC'), ('TAAGC', 'TAATC'), ('TAATA', 'TAATC')])
| Added by: | Peter Dawyndt |
| Date: | 2013-06-02 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


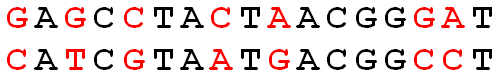
 RSS
RSS