SPOJ.com - Problem PROG0315

PROG0315 - Eyjafjallajökull

no tags

There is chaos in the air traffic centers of all European airports. Eyjafjallajökull — an ice-covered strato-volcano in Iceland — has just erupted. The ash cloud caused by this volcanic eruption is spreading rapidly across the European continent. A closure of the airspace over much of northern Europe is imminent. Your task is to identify whether any other volcanoes are likely to erupt and to follow the ash clouds they cause very closely. Based on this information, you must advise if can still be organized between two given airports.

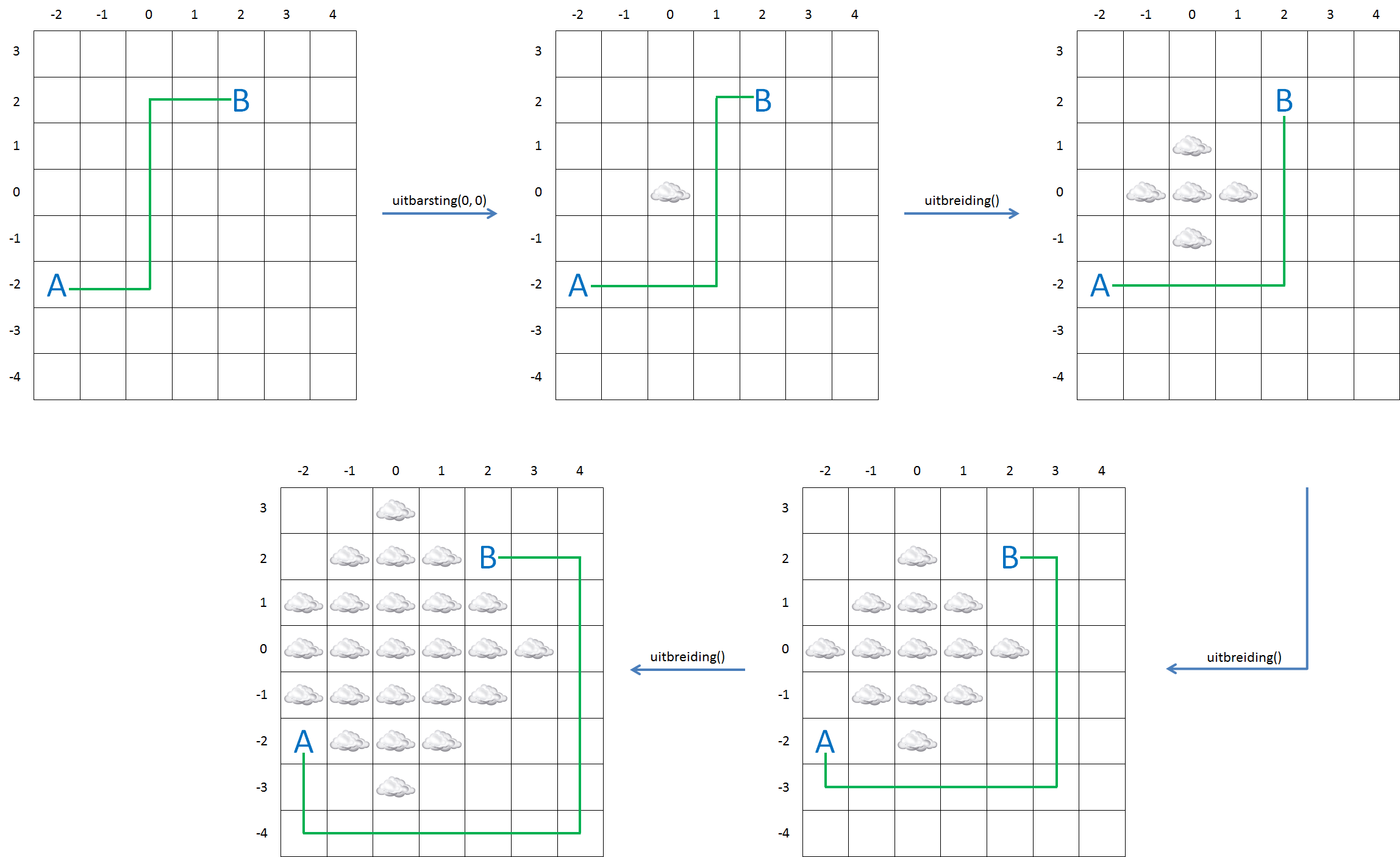
To maintain the overview, we have divided a map into square areas that form a rectangular grid. When a volcano erupts, we indicate this by drawing a cloud over the square where the volcano is situated. The spread of ash clouds is modeled by highlighting the squares that are at the top, at the bottom, on the left or on the right from the square that was already marked with a cloud in every following step. In order to keep things simple, we have numbered the columns in the example grid below in an increasing order from left to right and the rows from bottom to top. The order of the numbers has little importance for the rest of the exercise, as long as it is done with whole numbers in an increasing order. This way we can indicate a certain square with its column number and row number. The example shows how an ash cloud spreads over the adjacent squares after an eruption in square $(0, 0)$.

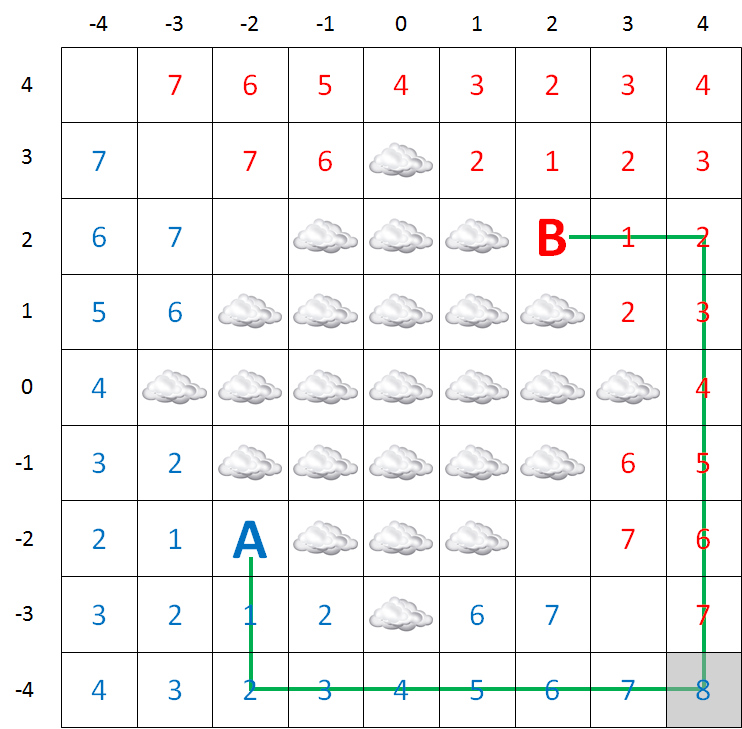
To advise whether any flights can be organized between two airports, you determine the distance of the shortest route from one airport to another without flying through the ash cloud. We will explain the procedure to determine this distance with the image below. The squares in which the airports are situated, are indicated with the letters A and B. A flying route can't go through any of the squares that are marked with clouds.

If one of the airports, or both of them, is situated in a square that is marked with a cloud, it is impossible to fly from that airports, otherwise, the shortest route cant be determined as follows:

mark the square A and B with the value 0 (zero)
equate $i$ with 0
mark every square that is above, below, left or right from A that is marked with a cloud, with value $i$ and give value $i + 1$ to every square that hasn't been marked yet; These markings are given in blue in the picture above.
mark every square that is above, below, left or right from B that is marked with a cloud, with value $i$ and give value $i + 1$ to every square that hasn't been marked yet; These markings are given in red in the picture above.
if no additional square can be numbered in step 3 or in step 4, both airports are completely isolated and no route can be found.
when there are two horizontally or vertically adjacent squares are marked one in blue and one in red in step 3 and 4, you have found the shortest route and the procedure ends.
raise $i$ with 1
return to 3

The only thing you have to think about yourself is how you will calculate the shortest distance that you have found in step 6. The distance of the route is expressed in the number of steps to adjacent squares (horizontally or vertically touching the current square). that you have to take to go from one airport to another. In the example above, the shortest route is 16.

Assignment

Define a class Map which can be used to follow the evolution of ash clouds over a rectangular square, an which can also be used to determine the shortest route — that doesn't go through an ash cloud — to get from one airport to another. The objects of this class must contain at least the following properties and methods.

Every object of the class Map must have the property ashcloud, that refers to a collection. When making a new object, this collection is empty, but the two following methods are used to change the contents of the collection.
A method eruption to which two whole numbers must be given, these numbers respectively indicate the column number $k$ and the row number $r$of a square in the grid in which the eruption takes place. The fact that this eruption causes an ash cloud, is saved by adding the tuple $(k, r)$ to the collection ash cloud.
A method spread to which no arguments should be given. By calling this method, the co-ordinates of all squares that were added to the collection ash cloud, that touch the square that was already indicated with an ash cloud on the left, on the right, above or below.
A method shortestRoute to which two tuples with the co-ordinates of the two airports must be given. The method must print the length of the shortest route between those airports, that does not go through the ash cloud. If one of both airports is situated beneath an ash cloud, or is both airports are completely isolated, the value -1 must be printed as a result.

Example

>>> airmap = Map()
>>> airmap.eruption(0, 0)
>>> airmap.ashcloud
{(0, 0)}
>>> airmap.spread()
>>> airmap.ashcloud
{(0, 1), (0, -1), (1, 0), (0, 0), (-1, 0)}
>>> airmap.shortestRoute((-2, -2), (2, 2))
8
>>> airmap.spread()
>>> airmap.ashcloud
{(0, 1), (-1, 1), (0, 0), (-1, 0), (-1, -1), (1, 1), (2, 0), (0, -2), (0, -1), (1, 0), (1, -1), (0, 2), (-2, 0)}
>>> airmap.shortestRoute((-2, -2), (2, 2))
12
>>> airmap.spread()
>>> airmap.shortestRoute((-2, -2), (2, 2))
16
>>> airmap.spread()
>>> airmap.shortestRoute((-2, -2), (2, 2))
-1

Er heerst chaos in de luchtverkeerscentra van alle Europese luchthavens. De Eyjafjallajökull — een met ijs bedekte stratovulkaan in IJsland — is net tot uitbarsting gekomen. De aswolk die bij deze vulkaanuitbarsting is ontstaan, verspreidt zich razendsnel over het Europese vasteland. Een sluiting van het luchtruim boven een groot deel van Noord-Europa dient zich dan ook aan. Jouw taak bestaat erin om in kaart te brengen of er nog andere vulkanen tot uitbarsting komen en de verspreiding van de aswolken die daardoor ontstaan op de voet te volgen. Op basis van deze informatie moet je adviseren of er nog vluchten kunnen georganiseerd worden tussen twee gegeven luchthavens.

Om het overzicht te bewaren, hebben we een kaart opgedeeld in vierkante gebieden die samen een rechthoekig rooster vormen. Als een vulkaan tot uitbarsting komt, dan duiden we dit aan door het vierkant waarin de vulkaan gelegen is te markeren met een wolk. De verspreiding van aswolken wordt gemodelleerd, door bij elke volgende tijdsstap ook de vierkanten met een wolk te markeren die bovenaan, onderaan, links of rechts raken aan een vierkant dat reeds met een wolk gemarkeerd was. We hebben voor de eenvoud de kolommen in het onderstaande voorbeeldrooster oplopend genummerd van links naar rechts, en de rijen oplopend van onder naar boven. De volgorde van de nummering doet er voor deze opgave verder weinig toe, zolang ze maar gebeurt met oplopende gehele getallen. Op die manier kunnen we immers een bepaald vierkant van het rooster aanduiden met diens kolom- en rijnummer. Het voorbeeld toont hoe een aswolk zich na een vulkaanuitbarsting in het vierkant $(0, 0)$ gradueel verspreidt over aangrenzende vierkanten.

Om te adviseren of er nog vluchten kunnen georganiseerd worden tussen twee luchthavens, bepaal je de afstand van de kortste route die nog kan genomen worden om van de ene luchthaven naar de andere te vliegen zonder daarbij door een aswolk te vliegen. We zullen de procedure om deze afstand te bepalen, uitleggen aan de hand van onderstaande figuur. De vierkanten waarin de twee luchthavens gelegen zijn, worden aangeduid met de letters A en B. Een vliegroute kan geen vierkanten aandoen die met een wolk gemarkeerd zijn.

Als één van de luchthavens, of beide, zelf in een vierkant liggen die met een wolk gemarkeerd is, dan is het niet meer mogelijk om vanaf die luchthaven te vliegen. Anders kan de kortste route op de volgende manier bepaald worden:

markeer de vierkanten A en B met de waarde 0 (nul)
stel $i$ gelijk aan 0
markeer elk vierkant dat bovenaan, onderaan, links of rechts raakt aan een vierkant rondom A dat gemarkeerd is met de waarde $i$ en dat zelf nog niet gemarkeerd is (met een wolk of een getal) met de waarde $i + 1$; deze markeringen worden in bovenstaande afbeelding in het blauw weergegeven
markeer elk vierkant dat bovenaan, onderaan, links of rechts raakt aan een vierkant rondom B dat gemarkeerd is met de waarde $i$ en dat zelf nog niet gemarkeerd is (met een wolk of een getal) met de waarde $i + 1$; deze markeringen worden in bovenstaande afbeelding in het rood weergegeven
als er in stap 3 of in stap 4 geen bijkomende vierkanten konden genummerd worden, dan zijn de luchthavens volledig van elkaar afgesloten door de aswolk en kan er geen route gevonden worden
van zodra er tijdens stap 3 of 4 twee horizontaal of verticaal aangrenzende vierkanten zijn waarvan de ene met een blauw getal en de andere met een rood getal gemarkeerd is, dan heb je de kortste route gevonden en eindigt de procedure
verhoog $i$ met 1
spring terug naar stap 3

Het enige waarover je zelf nog even moet nadenken is hoe je de afstand van de kortste route bepaalt die je in stap 6 hebt gevonden. De afstand van een route wordt uitgedrukt als het aantal stappen naar naburige vierkanten (horizontaal of verticaal rakend aan het huidige vierkant) dat je moet nemen om van de ene luchthaven naar een andere luchthaven te gaan. In bovenstaand voorbeeld is de kortste route dus 16.

Opgave

Definieer een klasse Kaart waarmee de evolutie van aswolken boven een rechthoekig rooster kan opgevolgd worden, en waarmee de kortste route tussen twee luchthavens — die niet door een aswolk loopt — kan bepaald worden. De objecten van deze klasse moeten minstens over de volgende eigenschappen en methoden beschikken:

Elk object van de klasse Kaart moet gegarandeerd een eigenschap aswolk hebben, die verwijst naar een verzameling. Bij het aanmaken van een nieuw object is deze verzameling nog leeg, maar de volgende twee methoden worden gebruikt om de inhoud van de verzameling te wijzigen.
Een methode uitbarsting waaraan twee gehele getallen moeten doorgegeven worden. Deze getallen geven respectievelijk het kolomnummer $k$ en rijnummer $r$ aan van een vierkant in het rooster waarin zich een vulkaanuitbarsting voordoet. Het feit dat hierdoor boven dit vierkant gebied een aswolk ontstaat, wordt bijgehouden door het tuple $(k, r)$ toe te voegen aan de verzameling aswolk.
Een methode uitbreiding waaraan geen argumenten moeten doorgegeven worden. Door het aanroepen van deze methode worden de coördinaten van alle vierkanten aan de verzameling aswolk toegevoegd, die zelf links, rechts, bovenaan of onderaan raken aan een vierkant dat reeds met een aswolk gemarkeerd was.
Een methode kortsteRoute waaraan twee tuples met de coördinaten van twee luchthavens moeten doorgegeven worden. De methode moet de lengte van de kortste route tussen de twee luchthavens teruggegeven, die niet door een aswolk passeert. Indien één van beide luchthavens zelf onder een aswolk ligt, of indien de twee luchthavens volledig van elkaar zijn afgesloten, dan moet de waarde -1 als resultaat teruggegeven worden.

Voorbeeld

>>> kaart = Kaart()
>>> kaart.uitbarsting(0, 0)
>>> kaart.aswolk
{(0, 0)}
>>> kaart.uitbreiding()
>>> kaart.aswolk
{(0, 1), (0, -1), (1, 0), (0, 0), (-1, 0)}
>>> kaart.kortsteRoute((-2, -2), (2, 2))
8
>>> kaart.uitbreiding()
>>> kaart.aswolk
{(0, 1), (-1, 1), (0, 0), (-1, 0), (-1, -1), (1, 1), (2, 0), (0, -2), (0, -1), (1, 0), (1, -1), (0, 2), (-2, 0)}
>>> kaart.kortsteRoute((-2, -2), (2, 2))
12
>>> kaart.uitbreiding()
>>> kaart.kortsteRoute((-2, -2), (2, 2))
16
>>> kaart.uitbreiding()
>>> kaart.kortsteRoute((-2, -2), (2, 2))
-1

Submit solution!

Added by:	Peter Dawyndt
Date:	2013-01-28
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None