PROG0239 - Stable marriage
A dating agency wants to pair off $n$ men $m_0, m_1, \ldots, m_{n-1}$ with $n$ women $w_0, w_1, \ldots, w_{n-1}$. Each man and each woman was asked to arrange all candidates of the opposite sex according to personal preference. These preferences can be represented in two$n \times n$ tables. The first row show the preferences of the men, for example the arrangement of man $m_0$, where a value $i$ ($0 \leq i < n$) in the first column shows that the first choice of man $m_0$ is woman $w_i$. A value $j$ ($0 \leq j < n$) in the second column shows that the man $m_0$'s second choice is woman $w_j$. In the same manner, the second row shows the arrangement of man $m_1$. The table with the preferences of the women drawn up in the same way.
Below are example tables with preferences of four men and four women, with the candidates of both groups labeled with the numbers 0, 1, 2, and 3.
| preference men | ||||
|---|---|---|---|---|
| 0 | 1 | 0 | 2 | 3 |
| 1 | 3 | 0 | 1 | 2 |
| 2 | 0 | 2 | 1 | 3 |
| 3 | 1 | 2 | 0 | 3 |
| preference women | ||||
|---|---|---|---|---|
| 0 | 0 | 2 | 1 | 3 |
| 1 | 2 | 3 | 0 | 1 |
| 2 | 3 | 1 | 2 | 0 |
| 3 | 2 | 1 | 0 | 3 |
From the previous tables, for example, we can see that man $m_0$ prefers woman $w_1$, while man $m_0$ is only the third choice of woman $w_1$.
Taking into account the personal preferences, the dating agency would like to pair off the men with the women. However, they want to do this in a way that no man and no woman would rather have each other than the partner they were paired off with. If successful, the chances are very high that this will indeed lead to stable marriages. For a very eloquent exposition of the stable marriage problem and additional background information, please read to this article.
Algorithm
In 1962 David Gale and Lloyd Shapley proved that for an equal number of men and women it is always possible to find a stable solution for the previous problem. They also provided an algorithm to fin the solution. This Gale-Shapley algorithm can be described as follows:
initially all men and women are available (not paired off)
as long as there is still a man m available
first find a woman W to whom the man m has not proposed yet (*)
if woman w has not yet been paired off with a man
then pair man m and woman w off
woman w is already otherwise paired off with male competitor c
if woman w prefers man m over man c
pair off man m aand woman w
man c is available again
otherwise woman w stays paired off with man c
Gale and Shapley also showed that at point (*) of the algorithm the woman $w$ has never before been proposed to by man $m$.
With the previous preference tables the algorithm follows these steps:
- iteration 1: man 0 chooses woman 1 (his first choice)
- iteration 2: man 1 chooses woman 3 (his first choice)
- iteration 3: man 2 chooses woman 0 (his first choice)
- iteration 4: man 3 chooses woman 1 (his first choice), because woman 1 prefers man 3 over man 0; man 0 is available again
- iteration 5: man 0 chooses woman 0 (his second choice), because woman 0 prefers man 0 over man 2; man 2 is available again
- iteration 6: man 2 chooses woman 2 (his second choice)
- all women are now paired off with men
- man 0 $\rightarrow$ woman 0
- man 1 $\rightarrow$ woman 3
- man 2 $\rightarrow$ woman 2
- man 3 $\rightarrow$ woman 1
Assignment
Write a function datingagency that implements the Gale-Shapley algorithm. To this function two parameters must be passed: the preference of the men and the preference of the women. Each of these parameters must be passed as a list of lists of integers, where the inner lists always display an arrangement of the values $0, 1, \ldots, n-1$. The function should return a tuple of couples (tuple with two integers), where the first element of the couple is the label of the man and the second element is the label of the woman the man is paired off with. The couples have to be arrange according to ascending labels of the men.
Example
>>> datingagency( ... [[1, 0, 2, 3], [3, 0, 1, 2], [0, 2, 1, 3], [1, 2, 0, 3]], ... [[0, 2, 1, 3], [2, 3, 0, 1], [3, 1, 2, 0], [2, 1, 0, 3]] ... ) ((0, 0), (1, 3), (2, 2), (3, 1)) >>> datingagency( ... [[0, 2, 1], [1, 0, 2], [1, 2, 0]], ... [[2, 1, 0], [2, 1, 0], [1, 2, 0]] ... ) ((0, 2), (1, 0), (2, 1)) >>> datingagency( ... [[0, 2, 1, 3], [2, 1, 3, 0], [0, 3, 1, 2], [1, 2, 0, 3]], ... [[1, 0, 2, 3], [0, 2, 3, 1], [3, 0, 1, 2], [1, 3, 2, 0]] ... ) ((0, 0), (1, 2), (2, 3), (3, 1))
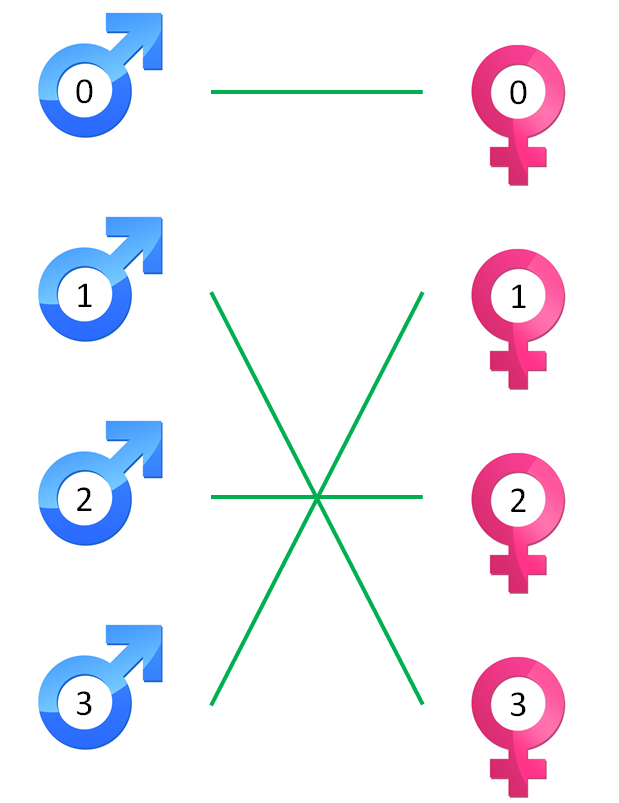
The first example corresponds with the preference tables above. The solution for these tables is shown graphically below.
Een koppelbureau wil $n$ mannen $m_0, m_1, \ldots, m_{n-1}$ koppelen aan $n$ vrouwen $v_0, v_1, \ldots, v_{n-1}$. Aan elke man en elke vrouw werd gevraagd om alle kandidaten van het andere geslacht te rangschikken naar persoonlijke voorkeur. Deze voorkeuren van de mannen en de vrouwen kunnen voorgesteld worden in twee $n \times n$ tabellen. Hierbij geeft de eerste rij van de tabel met de voorkeur van de mannen bijvoorbeeld de rangschikking van man $m_0$ aan, waarbij een waarde $i$ ($0 \leq i < n$) in de eerste kolom aangeeft dat de eerste keuze van man $m_0$ uitgaat naar vrouw $v_i$. Een waarde $j$ ($0 \leq j < n$) in de tweede kolom geeft analoog aan dat de tweede keuze van man $m_0$ uitgaat naar vrouw $v_j$. Op dezelfde manier geeft de tweede rij de rangschikking van de vrouwen zoals die werd opgesteld door man $m_1$. De tabel met de voorkeur van de vrouwen is op dezelfde manier opgebouwd.
Hieronder staan bijvoorbeeld de tabellen met de voorkeuren voor 4 mannen en 4 vrouwen, waarbij de kandidaten van beide groepen gelabeld worden met de getallen 0, 1, 2, en 3.
| voorkeur mannen | ||||
|---|---|---|---|---|
| 0 | 1 | 0 | 2 | 3 |
| 1 | 3 | 0 | 1 | 2 |
| 2 | 0 | 2 | 1 | 3 |
| 3 | 1 | 2 | 0 | 3 |
| voorkeur vrouwen | ||||
|---|---|---|---|---|
| 0 | 0 | 2 | 1 | 3 |
| 1 | 2 | 3 | 0 | 1 |
| 2 | 3 | 1 | 2 | 0 |
| 3 | 2 | 1 | 0 | 3 |
Uit voorgaande tabellen leiden we bijvoorbeeld af dat de eerste keuze van man $m_0$ uitgaat naar vrouw $v_1$, terwijl man $m_0$ zelf slechts de derde keuze is van vrouw $v_1$.
Rekening houdend met de persoonlijke voorkeuren wil het koppelbureau de mannen en de vrouwen paarsgewijs aan elkaar koppelen. Ze willen dit echter op zo'n manier doen dat geen enkele man en geen enkele vrouw liever elkaar zouden hebben dan de partner waaraan ze gekoppeld werden. Indien dit lukt, dan is de kans immers zeer groot dat dit zal leiden tot stabiele huwelijken. Voor een zeer welsprekende uiteenzetting van het stable marriage problem en bijkomende achtergrondinformatie verwijzen we naar dit artikel.
Algoritme
In 1962 bewezen David Gale en Lloyd Shapley dat het voor een gelijk aantal mannen en vrouwen altijd mogelijk is om een stabiele oplossing te vinden voor het bovenstaande probleem. Ze gaven daarbij ook een algoritme om de oplossing te vinden. Dit Gale-Shapley algoritme kan als volgt omschreven worden:
initieel zijn alle mannen en vrouwen nog vrij (niet gekoppeld)
zolang er nog een man m is die niet aan een vrouw gekoppeld is
zoek eerst gerangschikte vrouw v die man m nog niet heeft aangezocht (*)
als vrouw v nog niet gekoppeld is aan een man
koppel dan man m aan vrouw v
anders is vrouw v reeds gekoppeld aan mannelijke concurrent c
als vrouw v man m verkiest boven man c
koppel dan man m aan vrouw v
man c is terug een vrij man
anders blijft vrouw v aan man c gekoppeld
Gale en Shapley toonden ook aan dat er op punt (*) van het algoritme gegarandeerd steeds een vrouw $v$ is waaraan de vrije man $m$ nog geen aanzoek gedaan heeft.
Voor de bovenstaande voorkeurstabellen doorloopt het algoritme de volgende stappen:
- iteratie 1: man 0 kiest vrouw 1 (zijn eerste keuze)
- iteratie 2: man 1 kiest vrouw 3 (zijn eerste keuze)
- iteratie 3: man 2 kiest vrouw 0 (zijn eerste keuze)
- iteratie 4: man 3 kiest vrouw 1 (zijn eerste keuze), want vrouw 1 verkiest man 3 boven man 0; man 0 is terug vrij
- iteratie 5: man 0 kiest vrouw 0 (zijn tweede keuze), want vrouw 0 verkiest man 0 boven man 2; man 2 is terug vrij
- iteratie 6: man 2 kiest vrouw 2 (zijn tweede keuze)
- alle vrouwen zijn nu aan mannen gekoppeld
- man 0 $\rightarrow$ vrouw 0
- man 1 $\rightarrow$ vrouw 3
- man 2 $\rightarrow$ vrouw 2
- man 3 $\rightarrow$ vrouw 1
Opgave
Schrijf een functie koppelbureau die het Gale-Shapley algoritme implementeert. Aan deze functie moeten twee parameters doorgegeven worden: de voorkeur van de mannen en de voorkeur van de vrouwen. Elk van deze parameters moet doorgegeven worden als een lijst van lijsten van gehele getallen, waarbij de binnenste lijsten telkens een rangschikking van de waarden $0, 1, \ldots, n-1$ weergeven. De functie moet als resultaat een tuple van koppels (tuple met twee natuurlijke getallen) teruggeven, waarbij het eerste element van elk koppel telkens het label van de man aangeeft en het tweede element het label van de vrouw die aan de man gekoppeld werd. De koppels moeten gerangschikt worden volgens oplopende labels van de mannen.
Voorbeeld
>>> koppelbureau( ... [[1, 0, 2, 3], [3, 0, 1, 2], [0, 2, 1, 3], [1, 2, 0, 3]], ... [[0, 2, 1, 3], [2, 3, 0, 1], [3, 1, 2, 0], [2, 1, 0, 3]] ... ) ((0, 0), (1, 3), (2, 2), (3, 1)) >>> koppelbureau( ... [[0, 2, 1], [1, 0, 2], [1, 2, 0]], ... [[2, 1, 0], [2, 1, 0], [1, 2, 0]] ... ) ((0, 2), (1, 0), (2, 1)) >>> koppelbureau( ... [[0, 2, 1, 3], [2, 1, 3, 0], [0, 3, 1, 2], [1, 2, 0, 3]], ... [[1, 0, 2, 3], [0, 2, 3, 1], [3, 0, 1, 2], [1, 3, 2, 0]] ... ) ((0, 0), (1, 2), (2, 3), (3, 1))
Het eerste voorbeeld correspondeert met de voorkeurstabellen die hierboven als voorbeeld werden gegeven. De oplossing voor deze tabellen wordt hieronder grafisch weergegeven.
| Added by: | Peter Dawyndt |
| Date: | 2012-03-30 |
| Time limit: | 10s-15s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS