PROG0156 - Positioning
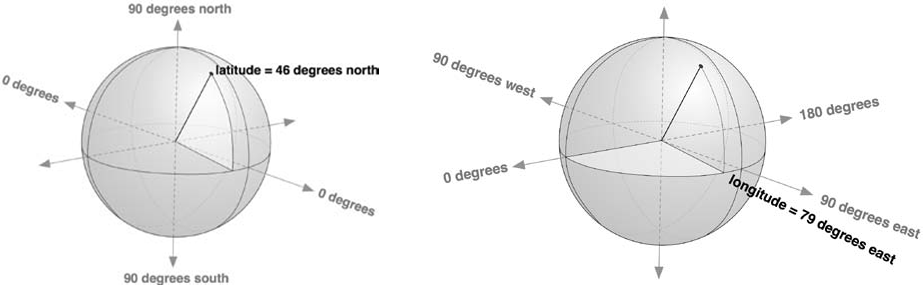
A place on Earth is indicated with spherical co-ordinates consisting of a pair of co-ordinates that respectively indicate the longitude an latitude. The latitude is the angle made by the joining line between that place and the centre of the Earth and the surface of the equator, and varies from -90° to 90° (both enclosed). The longitude is the angle between the meridian surface of Greenwich and the meridian surface of the measuring point and varies from -180° to 180° (half-open interval in which -180° is excluded).
In the most simple decimal notation a co-ordinate is given as a real number that indicates the number of degrees. Negative numbers indicate southern latitude or western longitude and the positive cases for northern latitude and the eastern longitude. In GMS notation a grade (*) is further divided in 60 minutes ('), and a minute is further divided in 60 seconds ("). To a latitude $b$ a s (southern latitude) is added if it is situated on the Southern Hemisphere ($?90° \leq b \leq 0°$), and an N (northern latitude) is added if it is situated on the Northern Hemisphere ($0° < b \leq 90°$). To a longitude $l$ a W (western longitude) is added if it is situated west of the prime meridian. If it is situated east of the prime meridian ($0° < l \leq 180°$), an e (eastern longitude) is added.
Assignment
- Write a function degrees2GMS
that converts a given co-ordinate $g$ ($g \in \mathbb{R}$, with $g \geq
0$) in decimal notation to the corresponding GMS notation. The
co-ordinate $g$ should be passed to the function as a real number. The
function should print a string of the format G*M'S"
as a result, as a representation of the co-ordinate in GMS notation. The
values $G$, $M$ and $S$ are calculated as follows:
- the number of degrees $G$ is the absolute value for the decimal point of $g$: $87,728055 = 87\ \text{graden}$
- multiply the part after the decimal point of $G$ by 60; the number of minutes $M$ is the part before the decimal point of the value in the outcome: $0,728055 \times 60 = 43,6833 = 43\ \text{minuten}$
- multiply the part after the decimal point by 60; the seconds $S$ are calculated by rounding off this number to the nearest integer: $0,6833 \times 60 = 40,998 = 41\ \text{seconden}$
- the final result is the string 87*43'41"
- Use the function degrees2GMS to write a function coord2GMS. Two real arguments should be passed to this function, that respectively represent the latitude and the longitude in decimal notation. As a result, the function must print a string that shows the location by giving both co-ordinates in GMS notation. For example, the function should print a string 40*26'46"N 79*56'56"W for the values 40,446195 and -79,948862. If an invalid longitude or latitude is given to the function, the string must print invalid as a result.
Example
>>> print(degrees2GMS(40.446195)) 40*26'46" >>> print(degrees2GMS(79.948862)) 79*56'56" >>> print(coord2GMS(40.446195, -79.948862)) 40*26'46"N 79*56'56"W >>> print(coord2GMS(-83.827439, -180.0)) invalid
Een plek op Aarde wordt in bolcoördinaten aangeduid met een paar coördinaten die respectievelijk de breedte- en lengtegraad aangeven. De breedtegraad is de hoek die de verbindingslijn tussen die plek en het middelpunt van de Aarde maakt met het vlak van de evenaar, en varieert van -90° tot 90° (beide ingesloten). De lengtegraad is de hoek tussen het meridiaanvlak van Greenwich en het meridiaanvlak van het meetpunt, en varieert van -180° tot 180° (halfopen interval waarin -180° wordt uitgesloten).
In de meest eenvoudige decimale notatie wordt een coördinaat aangegeven als een reëel getal dat het aantal graden aanduidt. Negatieve getallen staan voor zuiderbreedte of westerlengte, en positieve getallen voor noorderbreedte of oosterlengte. In GMS notatie wordt een graad (*) verder onderverdeeld in 60 minuten ('), en wordt een minuut verder onderverdeeld in 60 seconden ("). Aan een breedtegraad $b$ wordt een Z (zuiderbreedte) toegevoegd indien die op het zuidelijk halfrond gelegen is ($?90° \leq b \leq 0°$), en een N (noorderbreedte) indien die op het noordelijk halfrond gelegen is ($0° < b \leq 90°$). Aan een lengtegraad $l$ wordt een W (westerlengte) toegevoegd indien die ten westen van de nulmeridiaan gelegen is ($?180°< l \leq 0°)$ en een O (oosterlengte) indien die ten oosten van de nulmeridiaan gelegen is ($0° < l \leq 180°$).
Opgave
- Schrijf een functie graden2GMS die een gegeven coördinaat $g$ ($g \in \mathbb{R}$, met $g \geq 0$) in decimale notatie omzet naar de corresponderende GMS notatie. De coördinaat $g$ moet als reëel getal aan de functie doorgegeven worden. De functie moet als resultaat een string met formaat G*M'S" teruggeven, als voorstelling van de coördinaat in GMS notatie. De waarden $G$, $M$ en $S$ worden op de volgende manier berekend:
- het aantal graden $G$ is de absolute waarde van het deel voor het decimale punt van $g$: $87,728055 = 87\ \text{graden}$
- vermenigvuldig het deel na het decimale punt van $G$ met 60; het aantal minuten $M$ is het deel voor het decimale punt van de bekomen waarde: $0,728055 \times 60 = 43,6833 = 43\ \text{minuten}$
- vermenigvuldig het deel na het decimale punt van de minuten met 60; het aantal seconden $S$ wordt bekomen door dit getal af te ronden naar het dichtstbijzijnde natuurlijk getal: $0,6833 \times 60 = 40,998 = 41\ \text{seconden}$
- het finale resultaat is de string 87*43'41"
- Gebruik de functie graden2GMS om een functie coord2GMS te schrijven. Aan deze functie moeten twee reële argumenten meegegeven worden, die respectievelijk een breedte- en lengtegraad voorstellen uitgedrukt in decimale notatie. De functie moet als resultaat een string teruggeven die de plaatsbepaling gegeven door de twee coördinaten weergeeft in GMS notatie. Zo moet de functie voor de waarden 40,446195 en -79,948862 de string 40*26'46"N 79*56'56"W als resultaat teruggeven. Indien een ongeldige lengte- of breedtegraad wordt doorgegeven aan de functie, moet de string ongeldig als resultaat teruggegeven worden.
Voorbeeld
>>> print(graden2GMS(40.446195)) 40*26'46" >>> print(graden2GMS(79.948862)) 79*56'56" >>> print(coord2GMS(40.446195, -79.948862)) 40*26'46"N 79*56'56"W >>> print(coord2GMS(-83.827439, -180.0)) ongeldig
| Added by: | Peter Dawyndt |
| Date: | 2011-08-29 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS