SPOJ.com - Problem PROG0093

PROG0093 - Lunar phases

no tags

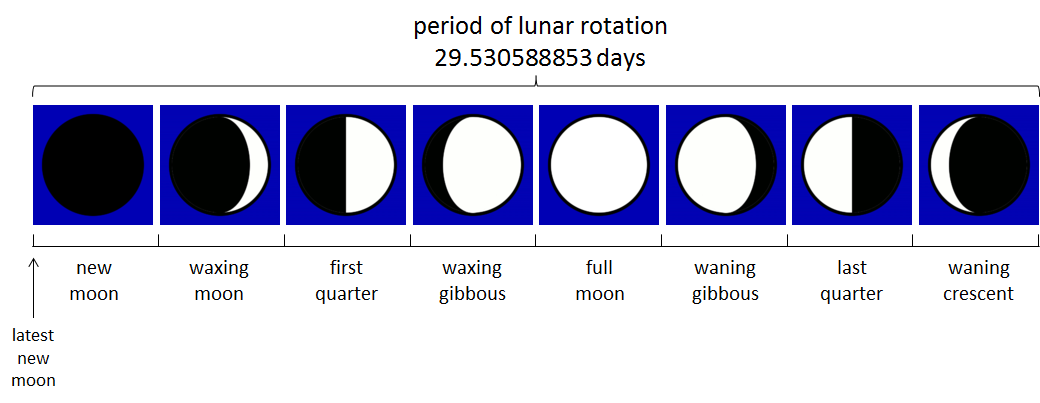
Lunar phase or phase of the moon refers to the shape of the illuminated (sunlit) portion of the Moon as seen by an observer, usually on Earth. The lunar phases change cyclically as the Moon orbits the Earth, according to the changing relative positions of the Earth, Moon, and Sun. The half of the lunar surface facing the Sun is always sunlit, but the portion of this illuminated hemisphere that is visible to an observer on Earth can vary from about 100% (full moon) to 0% (new moon). The lunar terminator is the boundary between the illuminated and unilluminated hemispheres. The period of the Moon orbiting the Earth is usually subdivided into eight lunar phases: new moon, waxing crescent, first quarter, waxing gibbous, full moon, waning gibbous, last quarter and waning crescent. If you can determine for a give date how many days have passed since the latest new moon, then the corresponding lunar phase may be determined by looking in which eighth of the period of the lunar rotation this number of days falls (see figure below).

Names of the lunar phases as applied in the Northern Hemisphere.

The Moon orbits the Earth with a period of $p=29.530588853$ days. If we know that there was a new moon at January 6, 2000, then we can use the following formula to determine the number of days since the last new moon. This number of days will be denoted as $d_n$. $$ d_n = d_r - p * \left\lfloor\frac{d_r}{p}\right\rfloor $$ Here, $d_r$ represents the number of days since the reference day January 6, 2000, and the operator $\lfloor x\rfloor$ determines the integer fraction of the floating point number $x$. Say, for example, that we want to determine the lunar phase on 28/01/2010. On this day, 3675 days have passed since January 6, 2000, so that $d_n=13,21$. Since the value $d_n$ falls within the fourth part of the eight-part division of the moon rotation period, this date corresponds to the lunar phase waxing gibbous.

Assignment

Write a function

lunarPhase([day][, month][, year])

that returns the name of the lunar phase corresponding to the given date. The day, the month and the year of the given date must be passed as three separate integer arguments to the function. All parameters of the function are optional, and by default get the value of today's day, month and year respectively. The current date must be determined dynamically, and should not be fixed for example to the date the function was implemented. If the function is called for example with arguments corresponding to the date of January 28th, 2010, the function must return the string waxing gibbous. Try to keep the number and the expression of the conditions that need to be tested in order to compute the result of the function as small as possible.

Hint: Take a look at the datetime module that is part of The Python Standard Library. In particular, take a look at what can be done with date objects — representing dates — and timedelta objects — representing time intervals. The following demo contains some clues on how these modules can be used to solve this assignment.

>>> from datetime import date
>>> today = date.today()
>>> type(today)
<type 'datetime.date'>
>>> today.year, today.month, today.day
(2011, 11, 18)
>>> birthday = date(1975, 12, 5)
>>> interval = today - birthday
>>> type(interval)
<type 'datetime.timedelta'>
>>> interval.days
13132
>>> 'Today I am {} days old'.format(interval.days)
'Today I am 13132 days old'

Example

>>> from datetime import date
>>> today = date.today()
>>> print(today)
2011-11-02
>>> lunarPhase(today.day, today.month, today.year)
'waxing moon'
>>> lunarPhase(2, 11, 2011)
'waxing moon'
>>> lunarPhase(day=2, month=11, year=2011)
'waxing moon'
>>> lunarPhase(year=2011, month=11, day=2)
'waxing moon'
>>> lunarPhase(month=11, day=2, year=2011)
'waxing moon'
>>> lunarPhase(2, year=2011, month=11)
'waxing moon'
>>> lunarPhase(month=8)
'new moon'
>>> lunarPhase(month=2)
'waning gibbous'
>>> lunarPhase(year=2020)
'full moon'
>>> lunarPhase(28, 1, 2009)
'new moon'
>>> lunarPhase(28, 1, 2010)
'waxing gibbous'
>>> lunarPhase(28, 1, 2011)
'last quarter'

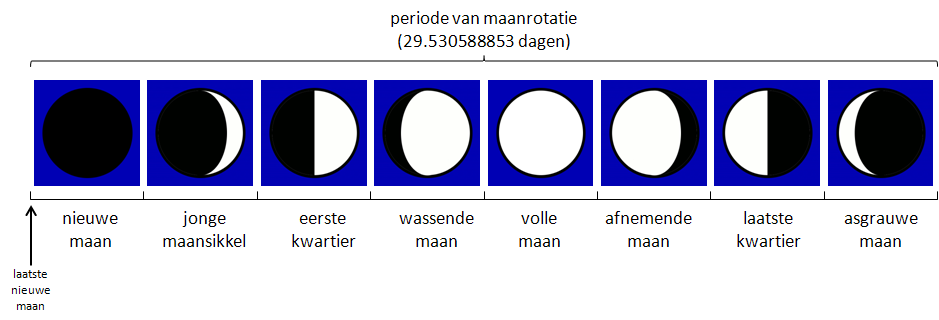
Onze maan vertoont zogenaamde schijngestalten, wat wil zeggen dat ze zich gedurende haar omloop rond de aarde in verschillende gedaanten laat zien. Dit fenomeen wordt veroorzaakt door het feit dat de maan vanuit een andere richting door de zon wordt bestraald dan de richting waarin ze wordt waargenomen. Hierdoor lijkt het alsof de terminator (dit is de scheidingslijn van licht en donker) zich over de oppervlakte van de maan verplaatst, waardoor de maan te zien is als een sikkelvormig of rond lichaam. De periode waarin de maan rond de aarde draait wordt over het algemeen onderverdeeld in acht maanfasen: nieuwe maan, jonge maansikkel, eerste kwartier, wassende maan, volle maan, afnemende maan, laatste kwartier en asgrauwe maan. Als je voor een gegeven datum kunt bepalen hoeveel dagen er zijn verstreken sinds de laatste nieuwe maan, dan kan je de corresponderende maanfase bepalen door te kijken in welke achtste deel van de periode van de maanrotatie dit aantal dagen valt (zie onderstaande figuur).

Benamingen van de schijngestalten van de maan, zoals die worden toegepast op het Noordelijk halfrond.

De maan draait in een baan om de aarde met een periode $p=29.530588853$ dagen. Als we weten dat er een nieuwe maan voorkwam op 6 januari 2000, dan kunnen we op basis van onderstaande formule het aantal dagen sinds de laatste nieuwe maan bepalen. We noteren dit aantal dagen als $d_n$. \[ d_n = d_r - p * \left\lfloor\frac{d_r}{p}\right\rfloor \] Hierbij stelt $d_r$ het aantal dagen voor sinds de referentiedatum van 6 januari 2000, en stelt de operator $\lfloor x\rfloor$ het geheel deel van het reëel getal $x$ voor. Stel dat we bijvoorbeeld de maanfase willen bepalen voor de datum 28/01/2010. Er zijn op deze datum reeds 3675 dagen verstreken sinds 6 januari 2000, waardoor in dit geval $d_n=13,21$. Aangezien de waarde van $d_n$ in het vierde deel van de achtdelige onderverdeling van de maanperiode valt, correspondeert deze datum dus met de maanfase wassende maan.

Opgave

Schrijf een functie

maanfase([dag][, maand][, jaar])

die de fase van de maan teruggeeft die correspondeert met een opgegeven datum. Aan deze functie moeten de dag, de maand en het jaar van de opgegeven datum als drie afzonderlijke integerargumenten doorgegeven worden. Alle parameters van de functie zijn optioneel, en krijgen als standaardwaarde de dag, de maand en het jaar van vandaag mee. Hierbij moet de datum van vandaag dynamisch bepaald worden, en niet vast ingesteld op bijvoorbeeld de dag waarop je de functie hebt geïmplementeerd. Indien de functie bijvoorbeeld wordt aangeroepen met argumenten die corresponderen met de datum 28 januari 2010, dan moet de string wassende maan als waarde teruggegeven worden. Probeer het aantal en de uitdrukking van de voorwaarden die moeten getest worden om het resultaat van de functie te bepalen zo beknopt mogelijk te houden.

Hint: Bestudeer de module datetime die meegeleverd wordt met The Python Standard Library. Bekijk in het bijzonder wat je allemaal kan doen met date objecten — die datums voorstellen — en timedelta objecten — die tijdsintervallen voorstellen. Onderstaande demo kan je waarschijnlijk al een deel op weg helpen.

>>> from datetime import date
>>> vandaag = date.today()
>>> type(vandaag)
<type 'datetime.date'>
>>> vandaag.year, vandaag.month, vandaag.day
(2011, 11, 18)
>>> geboortedatum = date(1975, 12, 5)
>>> aantal_dagen = vandaag - geboortedatum
>>> type(aantal_dagen)
<type 'datetime.timedelta'>
>>> aantal_dagen.days
13132
>>> 'Ik ben vandaag {} dagen oud'.format(aantal_dagen.days)
'Ik ben vandaag 13132 dagen oud'

Voorbeeld

>>> from datetime import date
>>> vandaag = date.today()
>>> print(vandaag)
2011-11-02
>>> maanfase(vandaag.day, vandaag.month, vandaag.year)
'jonge maansikkel'
>>> maanfase(2, 11, 2011)
'jonge maansikkel'
>>> maanfase(dag=2, maand=11, jaar=2011)
'jonge maansikkel'
>>> maanfase(jaar=2011, maand=11, dag=2)
'jonge maansikkel'
>>> maanfase(maand=11, dag=2, jaar=2011)
'jonge maansikkel'
>>> maanfase(2, jaar=2011, maand=11)
'jonge maansikkel'
>>> maanfase(maand=8)
'nieuwe maan'
>>> maanfase(maand=2)
'asgrauwe maan'
>>> maanfase(jaar=2020)
'volle maan'
>>> maanfase(28, 1, 2009)
'nieuwe maan'
>>> maanfase(28, 1, 2010)
'wassende maan'
>>> maanfase(28, 1, 2011)
'laatste kwartier'

Submit solution!

Added by:	Peter Dawyndt
Date:	2011-08-03
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None