PROG0090 - Triangle inequality
A carpenter has three wooden beams of different lengths. He wonders whether he can make a triangular frame without sawing the beams.
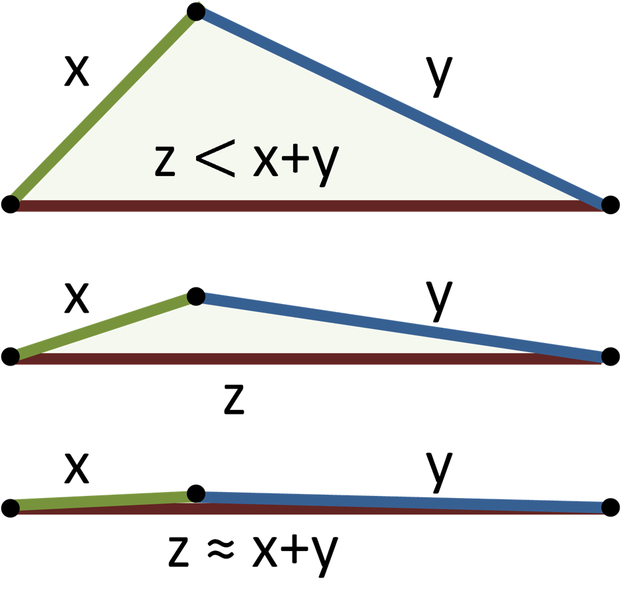
This will only be possible if triangle inequality applies to every one of the beams. For three sides $x$, $y$ and $z$ of the triangle this inequality states that $x + y > z$. In other words, a straight line is always the shortest distance between two points.
Input
The lengths of the wooden beams. These are real numbers that are each on a separate line. The numbers aren't necessarily ranked from smallest to largest.
Output
The statement "possible" or "impossible", depending on the possibility of forming a triangle with three beams.
Example
Input:
1.5 1.5 3.0
Output:
impossible
Example
Input:
4.0 6.0 5.0
Output:
possible
Een timmerman beschikt over drie houten balken van verschillende lengtes. Hij wil weten of hij hiermee een driehoekig frame in elkaar kan knutselen, zonder dat hij hierbij de balken moet verzagen.
Dit zal enkel kunnen als de driehoeksongelijkheid geldt voor elk van deze drie balken. Deze ongelijkheid zegt dat voor drie zijden $x$, $y$ en $z$ in een driehoek moet gelden dat $x + y > z$. Anders gezegd komt dit erop neer dat een rechte altijd de kortste afstand is tussen twee punten.
Invoer
De lengtes van de drie houten balken, gegeven als reële getallen die elk op een afzonderlijke regel staan. Merk op dat de lengtes niet noodzakelijk gerangschikt zijn van klein naar groot.
Uitvoer
De vermelding "mogelijk" of "onmogelijk" naargelang het al dan niet mogelijk is om met de drie balken een driehoek te vormen.
Voorbeeld
Invoer:
1.5 1.5 3.0
Uitvoer:
onmogelijk
Voorbeeld
Invoer:
4.0 6.0 5.0
Uitvoer:
mogelijk
| Added by: | Peter Dawyndt |
| Date: | 2011-08-03 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS