PROG0045 - Pozo Azul
Few people have heard of Pozo Azul, but for the past few summers, it has become the focus of attention of Europe's foremost cave-diving explorers. Some 30 miles north of Burgos lies the small village of Covanera, high among the headwaters of the Ebro Valley in northern Spain. It's a beautiful spot on the busy main road between Burgos and Santander, nestling beneath spectacularly sculpted cliffs at an altitude of about 700m. But unless you stop at the tiny Bar Muñecas — a staging post for explorers of Pozo Azul — beside the road, you'd never know that you were just a few hundred metres away from one of the longest cave dives in the world.
Pozo Azul is the most audacious exploratory cave-diving project of recent times and pushes the absolute limits of what is possible: it's serious stuff for all involved. Cave explorations progress slowly, depending on the location, the conditions, and the equipment, time and money available. The Spanish pioneered this cave in 1964, passing the spectacular first sump in 1979 and establishing Pozo Azul as the longest cave dive in the country. In 1991, another progression, by Spain’s GE Gaia team, took the cave's known length to a total of 1.780m.
Then, in the summer of 2001, British cave diver Jason Mallinson made a visit to the area. He had come to Spain shortly after his epic dives with Rick Stanton at the Emergence du Ressel in Lot, southwest France. Jason knew from the outset what was required to explore the cave further. Jason had invested seven years to gain a point 3.530m in Sump 2 when, in May 2008, a rival team of divers from Germany recognised the potential and mounted their own push on the cave. While they quickly proved their calibre by progressing a further 490m, their incursion to an ongoing project flew in the face of accepted protocol and soured relations within the diving community.
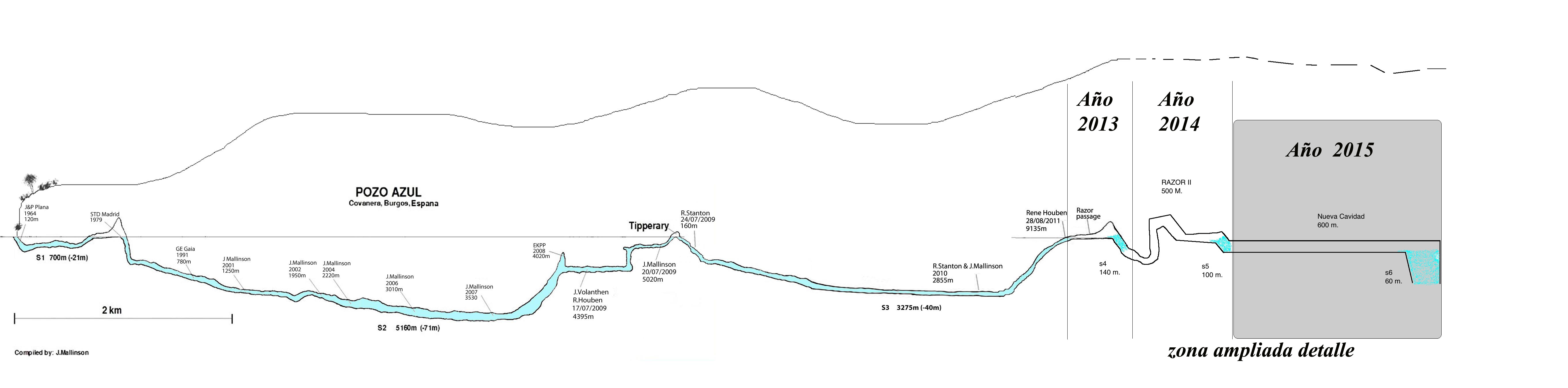
Jason Mallinson voelde zich hierdoor allerminst uit zijn lood geslagen. Met de Britten John Volanthen en Rick Stanton en de Nederlander René Houben verzamelde hij een team van ervaren grotduikers rond zich om in de tegenaanval te gaan. In 2009 slaagde het team er als eerste in om het 5.160m lange tweede reservoir volledig te doorkruisen en een droge galerij met de naam Tipperary te bereiken, waar ze een derde reservoir ontdekten. De 3.725m van dit derde reservoir konden ze voor het eerst oversteken in 2011. Ze vonden er een snelle stroom met verschillende watervallen die toegang gaf tot een vierde reservoir. Om dit punt te bereiken moest er in totaal 9.135m gedoken worden vanaf de ingang van de grot. In 2013 bereikten ze na tal van hindernissen het einde van het vierde reservoir, dat uiteindelijk slechts 140m lang bleek te zijn. Daarna volgde een snel stromende rivier met scherpe rotsen, en een vijfde reservoir dat in 2014 werd overwonnen. In 2015 ontdekte Jason Mallinson na een soloduik nog een zesde reservoir met daarachter een droge doorgang van minstens 1.000m. Meer dan ooit tevoren dringt de vraag zich op waar deze grot ooit zal stoppen.
Opgave
In deze opgave verwerken we dwarsdoorsneden waarop de verschillende gangen van een grot te zien zijn. Een dwarsdoorsnede wordt onderverdeeld in vierkanten die een rechthoekig $r \times k$ rooster vormen met $r$ rijen en $k$ kolommen. Elk vierkant bevat een deel van een gang die twee zijden van het vierkant met elkaar verbindt. De gang die door een vierkant loopt, omschrijven we met een string van twee verschillende hoofdletters die overeenkomen met de windrichtingen van de twee zijden van het vierkant die door de gang met elkaar verbonden worden: noord (N), zuid (Z), oost (O) en west (W). De ingang van de grot ligt steeds aan de noordzijde van het meest noordwestelijke vierkant. Hieronder zie je een voorbeeld van een dwarsdoorsnede van een grot, waarbij we de gangen zowel grafisch als met hun stringvoorstelling hebben weergegeven.
Je verkenningsopdracht bestaat erin de diepte van een grot te bepalen. De diepte van de grot wordt uitgedrukt als het aantal vierkanten dat je kan bereiken door de gang vanaf de ingang te volgen, totdat je ofwel niet meer verder kan of tegen de rand van de grot aanloopt. Hiervoor ga je als volgt te werk:
- Schrijf een functie dwarsdoorsnede waaraan twee argumenten moeten doorgegeven worden: i) een getal $r \in \mathbb{N}_0$ dat het aantal rijen van een rechthoekig rooster aangeeft en ii) een string die enkel bestaat uit de letters N, Z, O en W. De gegeven string is samengesteld uit de individuele stringvoorstellingen van de gangen van de grot, waarbij de vierkanten in het rechthoekige rooster van links naar rechts en van boven naar onder worden doorlopen. De functie moet een lijst teruggeven met de $r$ rijen van het rooster (opgelijst van noord naar zuid). Hierbij moet elke rij voorgesteld worden door een lijst met de stringvoorstelling van de opeenvolgende vierkanten (opgelijst van west naar oost). Indien op basis van de gegeven argumenten geen rechthoekig rooster kan gevormd worden, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige dwarsdoorsnede.
- Schrijf een functie diepte waaraan een omschrijving van de dwarsdoorsnede van een grot moet doorgegeven worden, voorgesteld als een lijst van lijsten zoals die door de functie dwarsdoorsnede wordt teruggegeven. De functie moet de diepte van de gegeven grot teruggeven.
Voorbeeld
De grot die beschreven wordt in het eerste deel van onderstaande voorbeeldsessie komt overeen met de grot die we hierboven grafisch voorgesteld hebben.
>>> grot = dwarsdoorsnede(4, 'NZZWNZZWNWNWOWZWNZZOOWZWOWZONZZWNONWNZNOOWOWZWZONWNOZOOWNWNWZOZW') >>> grot [['NZ', 'ZW', 'NZ', 'ZW', 'NW', 'NW', 'OW', 'ZW'], ['NZ', 'ZO', 'OW', 'ZW', 'OW', 'ZO', 'NZ', 'ZW'], ['NO', 'NW', 'NZ', 'NO', 'OW', 'OW', 'ZW', 'ZO'], ['NW', 'NO', 'ZO', 'OW', 'NW', 'NW', 'ZO', 'ZW']] >>> diepte(grot) 11 >>> dwarsdoorsnede(4, 'NZZWNZZWNWNWOWZWNZZ') Traceback (most recent call last): AssertionError: ongeldige dwarsdoorsnede
De naam Pozo Azul klinkt bij weinig mensen vertrouwd in de oren. Toch is het de afgelopen zomers een aantrekkingspool geweest voor de meest ervaren grotduikers van Europa. Onder de bovenloop van de Ebrovallei in het noorden van Spanje, ongeveer 30 mijl ten noorden van Burgos, ligt het klein dorpje Covanera. Het is een prachtige plek aan de drukke hoofdweg tussen Burgos en Santander, verscholen onder spectaculair gebeeldhouwde kliffen op een hoogte van ongeveer 700m. Tenzij je even halt houdt bij de kleine Bar Muñecas — de uitvalsbasis voor ontdekkingsreizigers van Pozo Azul — aan de rand van de weg, zou je nooit beseffen dat je slechts een paar honderd meter verwijderd bent van één van de langste onderwatergrotten ter wereld.
De verkenning van Pozo Azul is één van de meest gewaagde ondernemingen van de afgelopen decennia en helpt de grenzen verleggen van wat technisch gezien mogelijk is. Het verkennen van onderwatergrotten is immers een traag proces dat sterk afhankelijk is van de locatie, de omstandigheden, de apparatuur, en de beschikbare tijd en financiële middelen. Pozo Azul werd in 1964 voor het eerst verkend door Spanjaarden. Pas in 1979 slaagde men erin om het einde van het eerste spectaculaire reservoir met een lengte van 700m te bereiken, en daarmee van Pozo Azul de langste onderwatergrot in Spanje te maken. In 1991 bracht een ander Spaans team de lengte van het verkende gedeelte van de grot op 1.780m.
Tijdens de zomer van 2001 bracht de Britse grotduiker Jason Mallinson een bezoek aan de streek, kort na zijn epische duik met Rick Stanton aan het Emergence du Ressel in het departement Lot in zuidwest Frankrijk. Door zijn ervaring wist Jason maar al te goed wat er nodig was om nog dieper in de Pozo Azul te duiken dan iemand hem ooit had voorgedaan. Hij deed er zeven jaar over om 3.530m af te leggen in het tweede reservoir, tot er in mei 2008 plots een rivaliserend team duikers uit Duitsland opdook dat het potentieel van de grot inzag. Ze toonden vrij snel wat ze in hun mars hadden door nog eens 490m verder door te dringen dan het vorige record. Hun inbreuk in een lopend onderzoeksproject voelde echter als een kaakslag op een algemeen aanvaard protocol en verzuurde de relaties binnen de internationale duikersgemeenschap danig.
Jason Mallinson voelde zich hierdoor allerminst uit zijn lood geslagen. Met de Britten John Volanthen en Rick Stanton en de Nederlander René Houben verzamelde hij een team van ervaren grotduikers rond zich om in de tegenaanval te gaan. In 2009 slaagde het team er als eerste in om het 5.160m lange tweede reservoir volledig te doorkruisen en een droge galerij met de naam Tipperary te bereiken, waar ze een derde reservoir ontdekten. De 3.725m van dit derde reservoir konden ze voor het eerst oversteken in 2011. Ze vonden er een snelle stroom met verschillende watervallen die toegang gaf tot een vierde reservoir. Om dit punt te bereiken moest er in totaal 9.135m gedoken worden vanaf de ingang van de grot. In 2013 bereikten ze na tal van hindernissen het einde van het vierde reservoir, dat uiteindelijk slechts 140m lang bleek te zijn. Daarna volgde een snel stromende rivier met scherpe rotsen, en een vijfde reservoir dat in 2014 werd overwonnen. In 2015 ontdekte Jason Mallinson na een soloduik nog een zesde reservoir met daarachter een droge doorgang van minstens 1.000m. Meer dan ooit tevoren dringt de vraag zich op waar deze grot ooit zal stoppen.
Opgave
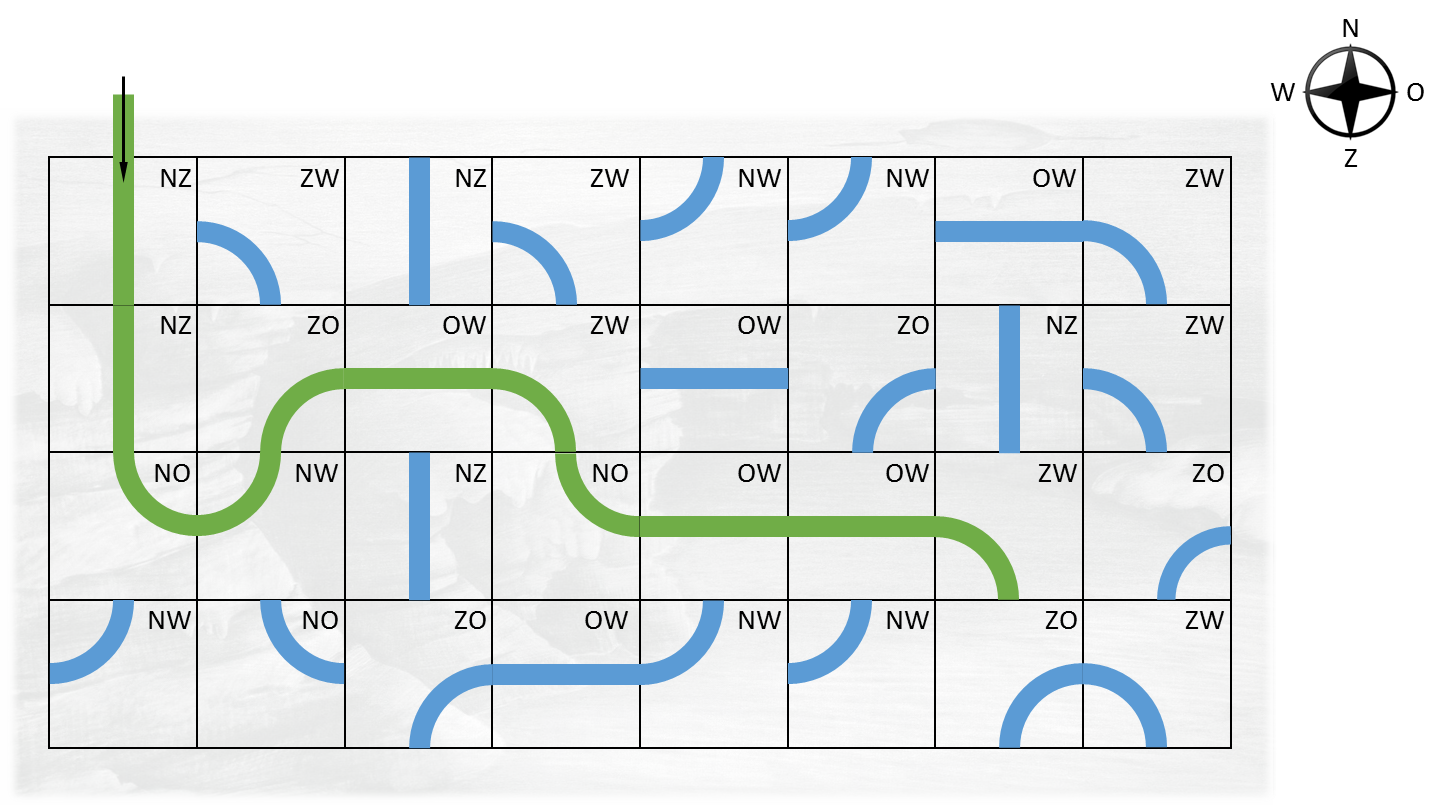
In deze opgave verwerken we dwarsdoorsneden waarop de verschillende gangen van een grot te zien zijn. Een dwarsdoorsnede wordt onderverdeeld in vierkanten die een rechthoekig $r \times k$ rooster vormen met $r$ rijen en $k$ kolommen. Elk vierkant bevat een deel van een gang die twee zijden van het vierkant met elkaar verbindt. De gang die door een vierkant loopt, omschrijven we met een string van twee verschillende hoofdletters die overeenkomen met de windrichtingen van de twee zijden van het vierkant die door de gang met elkaar verbonden worden: noord (N), zuid (Z), oost (O) en west (W). De ingang van de grot ligt steeds aan de noordzijde van het meest noordwestelijke vierkant. Hieronder zie je een voorbeeld van een dwarsdoorsnede van een grot, waarbij we de gangen zowel grafisch als met hun stringvoorstelling hebben weergegeven.
Je verkenningsopdracht bestaat erin de diepte van een grot te bepalen. De diepte van de grot wordt uitgedrukt als het aantal vierkanten dat je kan bereiken door de gang vanaf de ingang te volgen, totdat je ofwel niet meer verder kan of tegen de rand van de grot aanloopt. Hiervoor ga je als volgt te werk:
- Schrijf een functie dwarsdoorsnede waaraan twee argumenten moeten doorgegeven worden: i) een getal $r \in \mathbb{N}_0$ dat het aantal rijen van een rechthoekig rooster aangeeft en ii) een string die enkel bestaat uit de letters N, Z, O en W. De gegeven string is samengesteld uit de individuele stringvoorstellingen van de gangen van de grot, waarbij de vierkanten in het rechthoekige rooster van links naar rechts en van boven naar onder worden doorlopen. De functie moet een lijst teruggeven met de $r$ rijen van het rooster (opgelijst van noord naar zuid). Hierbij moet elke rij voorgesteld worden door een lijst met de stringvoorstelling van de opeenvolgende vierkanten (opgelijst van west naar oost). Indien op basis van de gegeven argumenten geen rechthoekig rooster kan gevormd worden, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige dwarsdoorsnede.
- Schrijf een functie diepte waaraan een omschrijving van de dwarsdoorsnede van een grot moet doorgegeven worden, voorgesteld als een lijst van lijsten zoals die door de functie dwarsdoorsnede wordt teruggegeven. De functie moet de diepte van de gegeven grot teruggeven.
Voorbeeld
De grot die beschreven wordt in het eerste deel van onderstaande voorbeeldsessie komt overeen met de grot die we hierboven grafisch voorgesteld hebben.
>>> grot = dwarsdoorsnede(4, 'NZZWNZZWNWNWOWZWNZZOOWZWOWZONZZWNONWNZNOOWOWZWZONWNOZOOWNWNWZOZW') >>> grot [['NZ', 'ZW', 'NZ', 'ZW', 'NW', 'NW', 'OW', 'ZW'], ['NZ', 'ZO', 'OW', 'ZW', 'OW', 'ZO', 'NZ', 'ZW'], ['NO', 'NW', 'NZ', 'NO', 'OW', 'OW', 'ZW', 'ZO'], ['NW', 'NO', 'ZO', 'OW', 'NW', 'NW', 'ZO', 'ZW']] >>> diepte(grot) 11 >>> dwarsdoorsnede(4, 'NZZWNZZWNWNWOWZWNZZ') Traceback (most recent call last): AssertionError: ongeldige dwarsdoorsnede
| Added by: | Peter Dawyndt |
| Date: | 2011-07-24 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS