PROG0041 - Plutokiller
The Kuiper belt is a ring of bodies in our Solar System that extends beyond the orbit of Neptune — the eight planet from the Sun. Pluto — the nineth planet from the Sun — was the first object to be discovered in the Kuiper belt. Correction, ex-planet, because in 2005 the International Astronomical Union (IAU) officially downgraded it to the status of dwarf planet.
Both the discovery of Pluto and its cancellation as a planet are due to the blink comparator, a viewing apparatus used by astronomers to find differences between two photographs of the night sky. It permits rapidly switching from viewing one photograph to viewing the other, "blinking" back and forth between the two taken of the same area of the sky at different times. This allows to more easily spot objects in the night sky that changed position. In photographs taken a few days apart, rapidly moving objects such as asteroids, comets and planets stand out because they are jumping back and forth between two positions, while all the other fixed stars stand still. This also relates to the fact that the term planet is derived from the Greek πλανήτης (planētēs), which itself goes back to πλανὰομαι (planáomai), meaning wandering. The animation below shows an example of a blink comparator that switches back and forth between two images taken by Clyde Tombaugh on January 23 and 29, 1930 at the Lowell Observatory. Note that he marked his discovery of Pluto with arrows.
Michael E. Brown, a professor of planetary astronomy at the California Institute of Technology (Caltech), has refined the idea of the blink comparator by learning a computer how to compare the photographs with each other. This way his team has discovered many trans-Neptunian objects, most notably, the dwarf planets Eris in the Kuiper belt and Sedna in the Oort cloud.
Brown had actually set himself as a target to discover a tenth planet in our Solar System, but ironically he did not increment but decrement the planet counter by one. The fact that Eris turned out to be 27% more massive than Pluto, led the IAU to define the term "planet" formally for the first time. This definition excluded Pluto and reclassified it as a member of the "dwarf planet" category. His twitter handle shows that Michael Brown has fully embraced the plutokiller nickname in the meantime.
Michael Brown published his memoirs about how he became responsible for the reclassification of Pluto from planet to dwarf planet in a 2010 book entitled How I Killed Pluto and Why It Had It Coming.
Assignment
In this assignment we will process text files containing photographs of the night sky. A photograph has $m$ lines containing $n$ characters each, and thus represents an $m \times n$ grid of characters. The grid contains a dash (-) occurs at positions where no star was observed in the photograph, and an asterisk (*) at positions where a star was observed in the photograph. If we index the rows of the grid from top to bottom, and the columns from left to right, we can represent the position of each star as the tuple $(r, k)$ containing its row index $r$ and column index $k$.
----------*- ----*-----*- ----*------- ------------ ------------ -*---*------ *-----*-*--- -**--------- ----*-*----- ------*-*--- *------**-*-
The above example shows two photographs taken a few days apart of the same area of the sky at different times, where one photographs covers the other. Click here to simulate a switch comparator that allows to switch between both photographs. Do you see the moving stars that we have highlighted in bold face? These are our candidate planet. The goal of this assignment is to automatically find these candidate planets using a computer. This is done in the following way:
- Write a function coordinates that takes the location of a text file containing a photograph of the night sky. The function must return a set containing the positions of all stars observed on the photograph.
- Write a function divergence that takes the locations of two text files containing photographs of the night sky. The function must return a tuple containing two sets. The first set must contain the positions of all stars observed on the first photograph and that are not on the second one. The second set must contain the positions of all stars observed on the second photograph and that are not on the first one.
- Write a function planets that takes the locations of two text files containing photographs of the night sky. The function must return a dictionary that has the positions of all stars observed on the second photograph and that are not on the first one as its keys. Each position $p$ that is used a key in the dictionary must be mapped to the set of all stars observed on the first photograph and that are not on the second one and that are closest to the position $p$. The distance between two positions $(r_1, k_1)$ and $(r_2, k_2)$ must be computed as $(r_1 - r_2)^2 + (k_1 - k_2)^2$.
- Write a function comparator that takes the locations of two text files containing photographs of the night sky. The function must return a string that represents an $m \times n$ grid made up of $m$ lines containing $n$ characters each. The values $m$ and $n$ correspond to the number of rows and columns in the two given photographs. The string returned by the function must represent the photograph obtained by overlaying the two given photographs. The positions in the grid where a fixed star occurs in the two given photographs must still be represented using an asterisk (*), but the positions where a star was only observed in the first photograph must be represented by the letter o, and the positions where a star was only observed in the second photograph must be represented by the letter n. The other positions must still be represented by a dash (-).
All functions that take the locations of two text files containing photographs of the night sky may assume that both photographs have the same size (same number of rows and columns) without having to check this explicitly.
Example
The following interactive session assumes that the text files photo1.txt and photo2.txt are located in the current directory.
>>> coordinates('photo1.txt') {(10, 8), (5, 5), (6, 8), (6, 6), (7, 1), (10, 7), (9, 8), (10, 10), (6, 0), (1, 4), (0, 10), (1, 10), (5, 1), (8, 6), (10, 0), (9, 6), (2, 4), (7, 2), (8, 4)} >>> coordinates('photo2.txt') {(10, 8), (4, 7), (6, 8), (7, 1), (10, 7), (10, 10), (9, 8), (6, 0), (0, 7), (1, 4), (7, 7), (8, 7), (1, 10), (5, 1), (10, 0), (9, 6), (2, 4), (7, 2), (8, 4)} >>> divergence('photo1.txt', 'photo2.txt') ({(8, 6), (5, 5), (0, 10), (6, 6)}, {(4, 7), (7, 7), (0, 7), (8, 7)}) >>> planets('photo1.txt', 'photo2.txt') {(4, 7): {(5, 5), (6, 6)}, (8, 7): {(8, 6)}, (7, 7): {(8, 6), (6, 6)}, (0, 7): {(0, 10)}} >>> print(comparator('photo1.txt', 'photo2.txt')) -------n--o- ----*-----*- ----*------- ------------ -------n---- -*---o------ *-----o-*--- -**----n---- ----*-on---- ------*-*--- *------**-*-
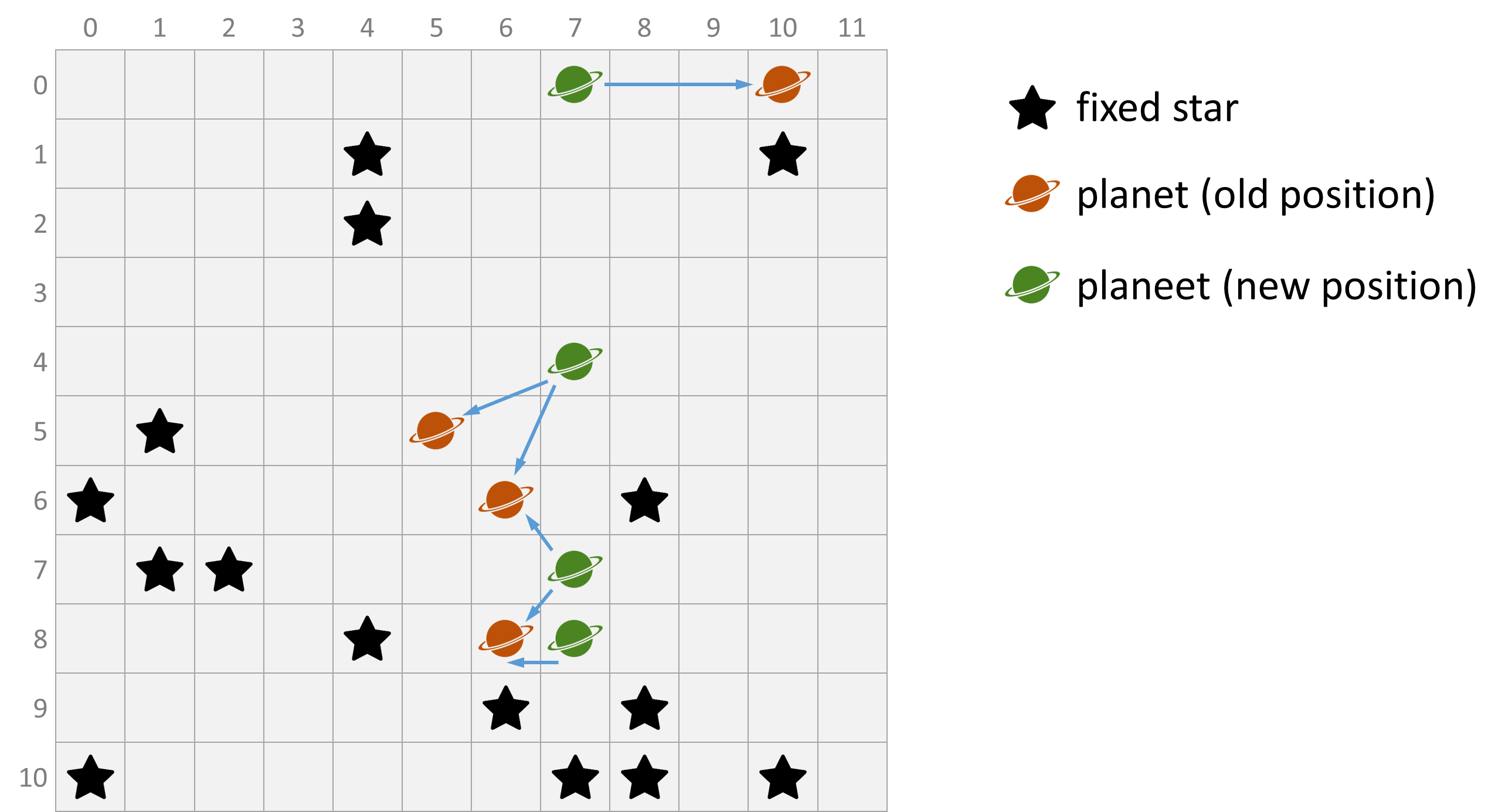
If we put the two photographs from the above example on top of each other, we obtain the result that is graphically represented in the figure below. The dictionary returned by the function planets represents a mapping that has been indicated using blue arrows.
Epilogue
This assignment first appeared during an examination on January 20, 2016. Coincidence or not, but on the very same day The Astronomical Journal published an article in which Michael E. Brown and his colleague Konstantin Batygin from the California Institute of Technology predict the location where a new planet must be located at the outskirts of our Solar System.
Now, Brown and Batygin need earthbound witnesses to confirm that Planet 9 exists. Just as Neptune was originally inferred by wobbles spotted in Uranus's orbit, the existence of Planet 9 can be inferred by the aligned Kuiper Belt objects. But without a verifiable observation, it's still a theoretical discovery. The pair are hoping to crowdsource that job, getting as many telescopes looking as possible across the globe. They've made the challenge easier by mapping Planet 9's orbit; now skywatchers have to pinpoint where it is on that very long path.
The name of the planet will be crowd-sourced too, if the researchers get their way — as opposed to being proposed by the discoverer and then approved by the International Astronomical Union (IAU), which is the usual way of doing things. Brown's and Batygin's personal name preference is "George", a hat-tip to British astronomer William Herschel, who discovered Uranus and wanted to name it Georgium Sidus (the Georgian Planet) after King George III. That might be a hard sell to the IAU — to say nothing of nearly all other stargazers, who tend to like a little more lyricism in their cosmos.
Whatever the planet is eventually called, its very existence will do more than simply add to the population of the solar system. It will also add to its mystery. Even in our tiny corner of the universe, it seems, there can still be big surprises lurking.
De Kuipergordel is een ring van hemellichamen voorbij de baan van Neptunus — de achtste planeet van ons zonnestelsel. Pluto — de negende planeet van ons zonnestelsel — was het eerste object dat in die gordel ontdekt werd. Correctie, ex-planeet, want in 2005 werd Pluto door de Internationale Astronomische Unie (IAU) officieel gedegradeerd tot dwergplaneet.
Zowel de ontdekking als de ondergang van Pluto als planeet zijn toe te schrijven aan de blink comparator, een toestel dat door sterrenkundigen gebruikt wordt om twee foto's van de nachtelijke hemel met elkaar te vergelijken. Door snel heen en weer te schakelen tussen foto's die met enkele dagen verschil genomen werden, valt het oog immers makkelijker op snel bewegende objecten zoals asteroïden, kometen en planeten omdat die heen en weer lijken te springen tussen twee posities, terwijl alle andere vaste sterren stilstaan. Daarmee gelinkt is het feit dat de term planeet afkomstig is van het Griekse πλανήτης (planētēs), dat zelf weer teruggaat op πλανὰομαι (planáomai), wat ronddolen of rondzwerven betekent. Hieronder zie je bijvoorbeeld een animatie van een blink comparator die schakelt tussen twee foto's die Clyde Tombaugh genomen heeft op 23 en 29 januari 1930 in het Lowell-observatorium, en waarop hij met pijltjes zijn ontdekking van Pluto heeft aangeduid.
De sterrenkundige Michael E. Brown verfijnde het idee van de blink comparator door niet zichzelf maar een computer aan het werk te zetten om foto's met elkaar te vergelijken. Op die manier hebben hij en zijn medewerkers tal van nieuwe transneptunische objecten ontdekt. Meest bekend zijn de dwergplaneten Eris in de Kuipergordel en Sedna in de Oortwolk.
Brown had zichzelf eigenlijk tot doel gesteld om een tiende planeet te ontdekken in ons zonnestelsel, maar ironisch genoeg zette hij de teller niet op +1 maar op -1. Het feit dat Eris een 27% grotere massa dan Pluto bleek te hebben, zette de IAU ertoe aan om voor het eerst een formele definitie van het begrip "planeet" op te stellen. Omdat Pluto niet aan deze definitie voldeed, werd ze vanaf dan geclassificeerd onder de dwergplaneten. Dat Michael Brown ondertussen zijn bijnaam van plutokiller volledig omarmd heeft, blijkt onder andere uit zijn twitterhandle.
Onder de titel How I Killed Pluto and Why It Had It Coming zette hij in 2010 zijn wedervaren als de man die Pluto de nek omdraaide om in boekvorm.
Opgave
In deze opgave werken we met tekstbestanden waarin foto's van de nachtelijke hemel zijn opgeslagen. Een foto bestaat uit $m$ regels die elk $n$ karakters bevatten, en stelt dus een $m \times n$ rooster van karakters voor. Waar geen ster wordt waargenomen op de foto staat een koppelteken (-) in het rooster. Waar wel een ster wordt waargenomen op de foto staat een sterretje (*) in het rooster. Als we de rijen van het rooster van boven naar onder nummeren vanaf nul, en de kolommen op dezelfde manier nummeren van links naar rechts, dan kunnen we de positie van een ster aanduiden met een tuple $(r, k)$. Daarbij staat $r$ voor het rijnummer en $k$ voor het kolomnummer van de ster in het rooster.
----------*- ----*-----*- ----*------- ------------ ------------ -*---*------ *-----*-*--- -**--------- ----*-*----- ------*-*--- *------**-*-
Hierboven zie je bijvoorbeeld twee foto's die met enkele dagen verschil werden genomen, waarbij de ene foto de andere bedekt. Klik hier om net zoals met een blink comparator te schakelen tussen deze twee foto's. Kan je de bewegende sterren waarnemen die we ook in het vet hebben aangeduid? Dat zijn onze kandidaat-planeten. Het doel van deze opgave is om deze kandidaat-planeten met de computer op te sporen. Hiervoor ga je als volgt te werk:
- Schrijf een functie coordinaten waaraan de locatie van een tekstbestand met een foto van de nachtelijke hemel moet doorgegeven worden. De functie moet een verzameling teruggeven die de posities bevat van alle sterren die op de foto kunnen waargenomen worden.
- Schrijf een functie afwijkingen waaraan de locaties van twee tekstbestanden met foto's van de nachtelijke hemel moeten doorgegeven worden. De functie moet een tuple met twee verzamelingen teruggeven, waarbij de eerste verzameling de posities bevat van alle sterren die op de eerste foto worden waargenomen en niet op de tweede, en de tweede verzameling de posities van alle sterren die op de tweede foto worden waargenomen en niet op de eerste.
- Schrijf een functie planeten waaraan de locaties van twee tekstbestanden met foto's van de nachtelijke hemel moeten doorgegeven worden. De functie moet een dictionary teruggeven waarvan de sleutels gevormd worden door de posities van de sterren die op de tweede foto worden waargenomen en niet op de eerste. Elke positie $p$ die als sleutel gebruikt wordt in de dictionary moet afgebeeld worden op de verzameling van posities van sterren die op de eerste foto worden waargenomen en niet op de tweede en die het dichtst bij de positie $p$ liggen. Hierbij wordt de afstand tussen twee posities $(r_1, k_1)$ en $(r_2, k_2)$ bepaald als $(r_1 - r_2)^2 + (k_1 - k_2)^2$.
- Schrijf een functie comparator waaraan de locaties van twee tekstbestanden met foto's van de nachtelijke hemel moeten doorgegeven worden. De functie moet een string teruggeven die een $m \times n$ rooster voorstelt bestaande uit $m$ regels die elk $n$ karakters bevatten. Hierbij zijn $m$ en $n$ respectievelijk het aantal rijen en kolommen van de twee gegeven foto's. De string die door de functie wordt teruggegeven moet de foto voorstellen die men bekomt door de twee gegeven foto's als het ware bovenop elkaar te leggen. De posities in het rooster waar een vaste ster voorkomt op beide foto's moeten nog steeds voorgesteld worden door een sterretje (*), maar de posities waar enkel een ster voorkomt op de eerste foto moeten voorgesteld worden door de letter o en de posities waar enkel een ster voorkomt op de tweede foto moeten voorgesteld worden door de letter n. De andere posities moeten nog steeds voorgesteld worden door een koppelteken (-).
Alle functies waaraan locaties van twee tekstbestanden met foto's van de nachtelijke hemel moeten doorgegeven worden, mogen ervan uitgaan dat deze foto's even groot zijn (evenveel rijen en kolommen) zonder dat ze dit zelf expliciet moeten controleren.
Voorbeeld
In onderstaande voorbeeldsessie gaan we ervan uit dat de tekstbestanden foto1.txt en foto2.txt zich in de huidige directory bevinden.
>>> coordinaten('foto1.txt') {(10, 8), (5, 5), (6, 8), (6, 6), (7, 1), (10, 7), (9, 8), (10, 10), (6, 0), (1, 4), (0, 10), (1, 10), (5, 1), (8, 6), (10, 0), (9, 6), (2, 4), (7, 2), (8, 4)} >>> coordinaten('foto2.txt') {(10, 8), (4, 7), (6, 8), (7, 1), (10, 7), (10, 10), (9, 8), (6, 0), (0, 7), (1, 4), (7, 7), (8, 7), (1, 10), (5, 1), (10, 0), (9, 6), (2, 4), (7, 2), (8, 4)} >>> afwijkingen('foto1.txt', 'foto2.txt') ({(8, 6), (5, 5), (0, 10), (6, 6)}, {(4, 7), (7, 7), (0, 7), (8, 7)}) >>> planeten('foto1.txt', 'foto2.txt') {(4, 7): {(5, 5), (6, 6)}, (8, 7): {(8, 6)}, (7, 7): {(8, 6), (6, 6)}, (0, 7): {(0, 10)}} >>> print(comparator('foto1.txt', 'foto2.txt')) -------n--o- ----*-----*- ----*------- ------------ -------n---- -*---o------ *-----o-*--- -**----n---- ----*-on---- ------*-*--- *------**-*-
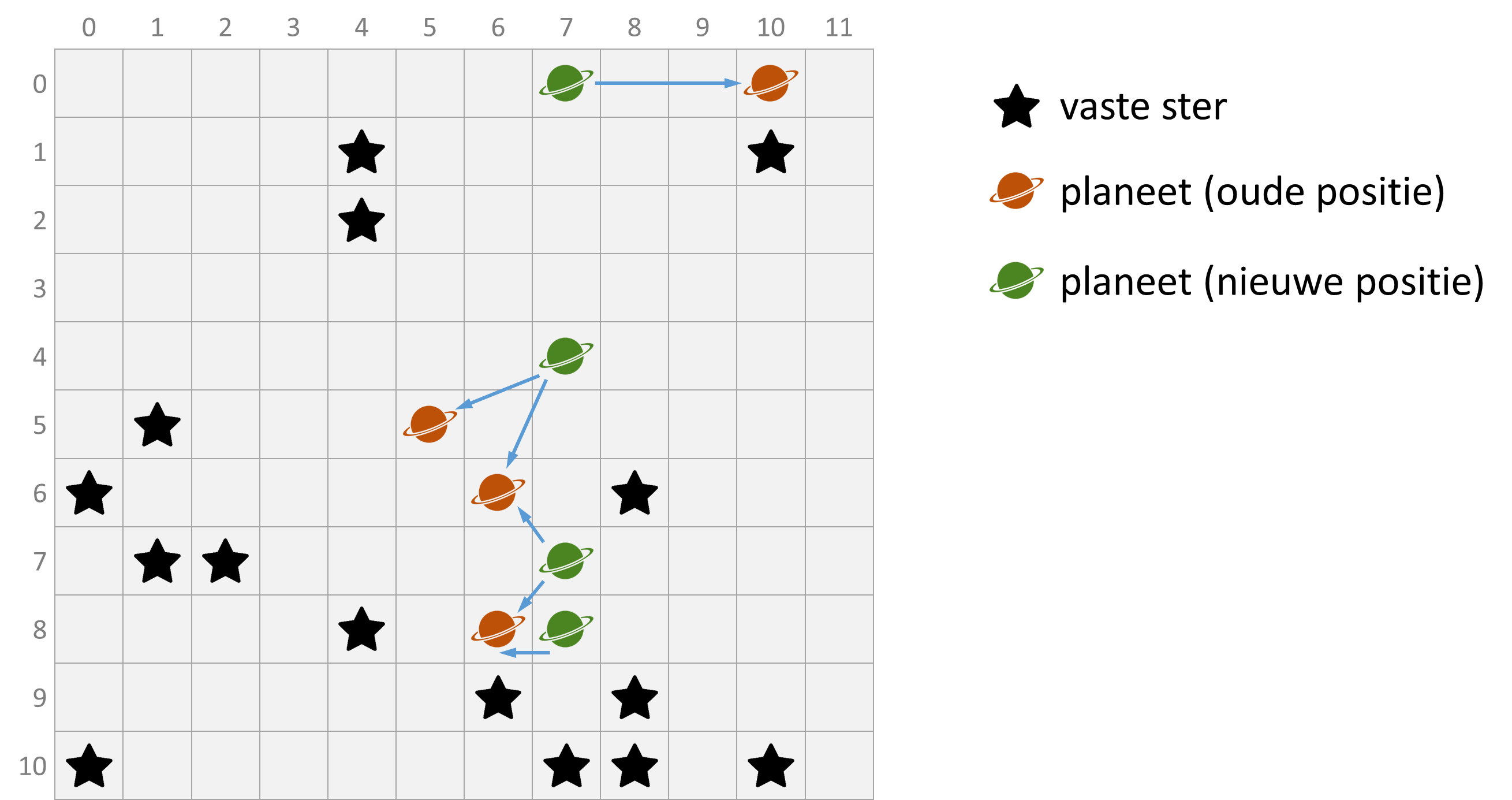
Als we de twee foto's uit bovenstaand voorbeeld bovenop elkaar leggen, dan bekomen we het resultaat dat hieronder grafisch wordt weergegeven. De dictionary die door de functie planeten wordt teruggegeven, stelt een afbeelding voor die we hebben aangeduid met blauwe pijlen.
Epiloog
Deze opgave verscheen voor het eerst op een examen van 20 januari 2016. Toeval of niet, maar op diezelfde dag publiceerde het tijdschrift The Astronomical Journal een artikel waarin Michael E. Brown en zijn collega Konstantin Batygin van het California Institute of Technology een voorspelling maken van waar er zich ergens aan de buitenkant van ons zonnestelselsel een nieuwe planeet moet bevinden.
Nu moeten Brown en Batygin enkel nog bevestiging zien te krijgen dat Planeet 9 daadwerkelijk bestaat aan de hand van een waarneming vanop Aarde. Net zoals de positie van Neptunus oorspronkelijk werd afgeleid uit fluctuaties in de baan van Uranus, kan het bestaan van Planeet 9 afgeleid worden uit het feit dat een aantal recent ontdekte Kuipergordelobjecten in hetzelfde vlak rond de zon draaien. Maar zonder een controleerbare waarneming blijft Planeet 9 nog steeds een theoretische ontdekking. De twee onderzoekers hopen die waarneming te crowsourcen door zoveel mogelijk telescopen naar de planeet te laten speuren. Ze hebben de zoektocht vergemakkelijkt door de baan van de planeet in kaart te brengen, waardoor skywatchers enkel nog moeten uitzoeken waar de planeet zich ergens op deze baan bevindt.
Als de onderzoekers hun zin krijgen, dan zal ook de keuze voor de naam van de planeet worden gecrowsourced, in tegenstelling tot de traditie dat deze naam wordt gegeven door de ontdekker en daarna wordt goedgekeurd door de IAU. De persoonlijke voorkeur van Brown en Batygin valt op de naam "George", een vette knipoog naar de ontdekker van de planeet Uranus, de Britse sterrenkundige William Herschel, die zijn planeet Georgium Sidus (de Georgiaanse Planeet) wilde vernoemen naar George III. Dat lijkt echter moeilijk te verkopen aan de IUA — om maar te zwijgen van alle andere sterrenspotters die graag een beetje meer lyriek zien in de kosmos.
Wat de uiteindelijke naam van de planeet ook wordt, het feit dat ze zou bestaan zal in ieder geval meer doen dan de teller van het aantal planeten in ons zonnestelsel terug op negen zetten. Het zal de mystiek van ons zonnestelsel weer doen toenemen, als blijkt dat er zelfs in de kleinste uithoek van ons universum nog steeds grote verrassingen op de loer liggen.
| Added by: | Peter Dawyndt |
| Date: | 2011-07-24 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS