PROG0037 - Lemmings
Lemmings — a species of small rodents — are known to have periodic population booms. They reproduce so quickly that their population fluctuations are chaotic, rather than following linear growth to a carrying capacity or regular oscillations. It is not known why lemming populations fluctuate with such great variance roughly every four years, before numbers drop to near extinction. If an overpopulation of lemmings occurs in a certain area, they disperse in all directions, seeking food and shelter their natural habitats can no longer provide. These mass migrations are so striking that lemmings have become the subject of widely popular misconceptions that go back many centuries. In the 1530s, the geographer Zeigler of Strasbourg proposed the theory that the creatures fell out of the sky during stormy weather (also featured in the folklore of the Inupiat/Yupik at Norton Sound), and then died suddenly when the grass grew in spring. This description was contradicted by the natural historian Ole Worm, who accepted that lemmings could fall out of the sky, but claimed they had been brought over by the wind rather than created by spontaneous generation.
The misconception of lemming "mass suicide" is long-standing and has been popularized by a number of factors. Most influential was the 1958 Disney film White Wilderness — which won an Academy Award for Documentary Feature — in which footage was shown with lemmings jumping into certain death after scenes of mass migration. However, the documentary Cruel Camera found out that the lemmings used for White Wilderness were flown from Hudson Bay to Calgary, Alberta, Canada, where they did not jump off the cliff, but were in fact forced off the cliff by the camera crew. Because of the limited number of lemmings at their disposal, which in any case were the wrong subspecies, the migration scenes were simulated using tight camera angles and a large, snow-covered turntable.
These stories about lemmings inspired the Scottish software company DMA Design (currently known as Rockstar North Ltd.) to develop the video game Lemmings. Lemmings was one of the best-received video games of the early 1990s. The objective of the game is to guide a group of anthropomorphised lemmings through a number of obstacles to a designated exit. Each level begins with a trap door opening from above, releasing a steady line of lemmings who all follow each other. To save the required number of lemmings to win, one must determine how to assign a limited number of eight different skills to specific lemmings that allow the selected lemming to alter the landscape, to affect the behaviour of other lemmings, or to clear obstacles to create a safe passage for the rest of the lemmings.
Assignment
In this assignment we ask you to perform a simplified simulation of a lemming in a level of the video game Lemmings. A level of the video game consists of a number of cells that are arranged in a rectangular grid, and is described in a text file. In that description free cells are represented by a space, and cells containing an obstacle are represented by a hash symbol (#). Cells along the outer edge of the grid always contain an obstacle. A level might thus be represented in the following way.
################################# # # # # # # ### # ########### ### # ########### ######## # ########### ############## # #################################
Because each level has a rectangular shape, we will indicate positions of cells in the level by numbering the rows of the rectangle from top to bottom, and the columns from left to right, starting from zero. For our example level, the rows and columns are numbered as follows.
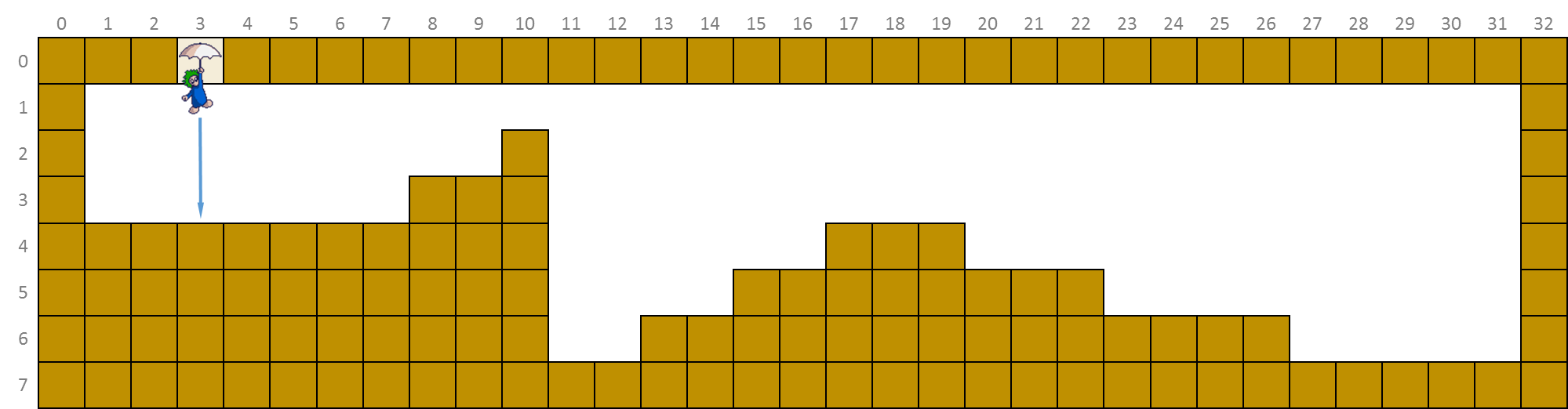
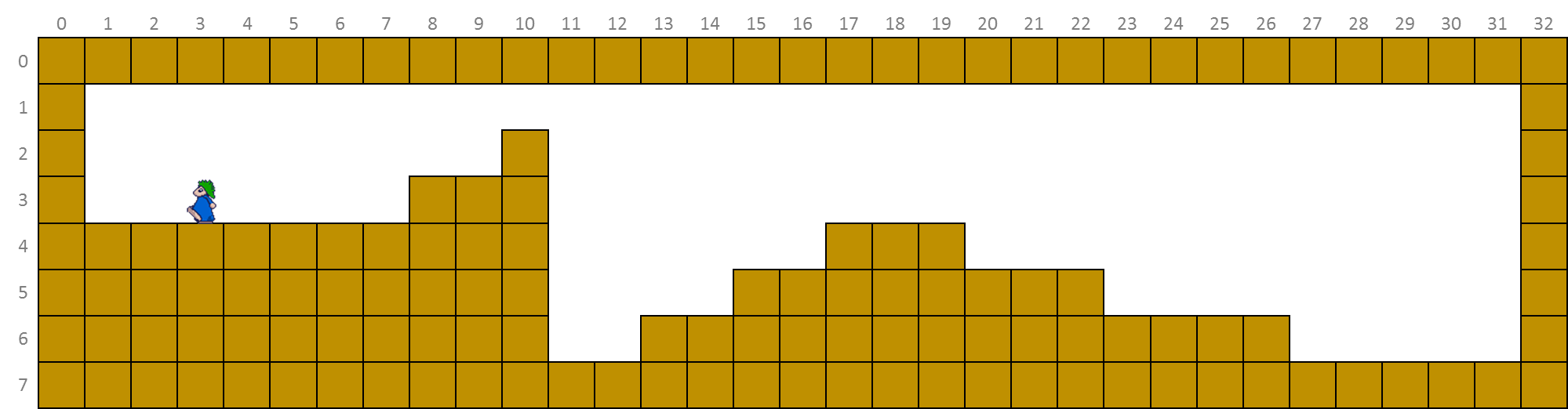
If we drop a lemming in the level through a trap door opening from above in column 3, the lemming falls down until it hits solid ground at position $(3, 3)$. If the lemming initially starts moving towards the left, the situation of the level at that point in time looks like this.
During each simulation step the lemming autonomously moves in a certain direction. Suppose the lemming wants to move to the right, there are three possible options that are illustrated in the figure below.
We call the cell where the lemming is currently located the current cell. If the cell to the right of the current cell is free (as in the left figure above), the lemmings moves to this cell. Then, the lemming falls down until it hits solid ground (if that was not already the case). If the cell to the right of the current cell contains an obstacle but the cell above the obstacle is free (as in the middle figure above), the lemming moves to that free cell. If both cells to the right and to upper right of the current cell contain an obstacle, the lemming stays in the current cell but now starts moving to the left. The lemming behaves in the same way if it wants to move to the left during the next step of the simulation.
You are asked to define a class Lemming that can be used to simulate a lemming in a given level of the video game Lemmings. This class must support at least the following methods:
- An initialization method that takes three arguments: i) the location of a text file containing a description of the level, ii) the column where the lemming is initially dropped into the level through a trap door opening from above and iii) the direction in which the lemming initially wants to move. The direction is indicated by a less than symbol (<) if the lemming initially wants to move to the left and by a greater than symbol (>) if the lemming initially wants to move to the right. After execution of the initialization method, the lemming must always have solid ground under his feet.
- A method position that returns a tuple of three elements: i) row index of the cell where the lemming is currently located, ii) column index of the cell where the lemming is currently located and iii) direction in which the lemming currently moves, indicated by a less than or a greater than symbol (same meaning as for the initialization method).
- A method step that can be used to simulate a single step of the lemming. The method must return a tuple containing the position and direction of the lemming after the step has been taken, where the tuple has the same format used for the return value of the method position.
- A method steps that takes an integer $n \in \mathbb{N}$. The method must simulate $n$ steps of the lemming, and return a list containing the positions and directions of the lemming after each step has been taken. The position and direction of the lemming must be represented by a tuple that has the same format used for the return value of the method position.
In addition, it must be possible to use the built-in function print to generate a string representation of the current position and direction of the lemming in the level. This string representation must display the level in the same way as it is represented in the given text file. The position where the lemming is currently located must be represented by a less than symbol (<) if the lemming currently moves to the left and by a greater than symbol (>) if the lemming currently moves to the right.
Example
In the following interactive session, we assume that the text file level.txt is located in the current directory.
>>> lemming = Lemming('level.txt', 3, '<') >>> lemming.position() (3, 3, '<') >>> print(lemming) ################################# # # # # # # < ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.step() (3, 2, '<') >>> lemming.step() (3, 1, '<') >>> lemming.step() (3, 1, '>') >>> lemming.step() (3, 2, '>') >>> print(lemming) ################################# # # # # # # > ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.steps(5) [(3, 3, '>'), (3, 4, '>'), (3, 5, '>'), (3, 6, '>'), (3, 7, '>')] >>> print(lemming) ################################# # # # # # # >### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.step() (2, 8, '>') >>> print(lemming) ################################# # # # > # # # ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.step() (2, 9, '>') >>> lemming.step() (1, 10, '>') >>> print(lemming) ################################# # > # # # # # ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.step() (6, 11, '>') >>> print(lemming) ################################# # # # # # # ### # ########### ### # ########### ######## # ###########> ############## # ################################# >>> lemming.steps(21) [(6, 12, '>'), (5, 13, '>'), (5, 14, '>'), (4, 15, '>'), (4, 16, '>'), (3, 17, '>'), (3, 18, '>'), (3, 19, '>'), (4, 20, '>'), (4, 21, '>'), (4, 22, '>'), (5, 23, '>'), (5, 24, '>'), (5, 25, '>'), (5, 26, '>'), (6, 27, '>'), (6, 28, '>'), (6, 29, '>'), (6, 30, '>'), (6, 31, '>'), (6, 31, '<')] >>> lemming.steps(21) [(6, 30, '<'), (6, 29, '<'), (6, 28, '<'), (6, 27, '<'), (5, 26, '<'), (5, 25, '<'), (5, 24, '<'), (5, 23, '<'), (4, 22, '<'), (4, 21, '<'), (4, 20, '<'), (3, 19, '<'), (3, 18, '<'), (3, 17, '<'), (4, 16, '<'), (4, 15, '<'), (5, 14, '<'), (5, 13, '<'), (6, 12, '<'), (6, 11, '<'), (6, 11, '>')] >>> print(lemming) ################################# # # # # # # ### # ########### ### # ########### ######## # ###########> ############## # #################################
The following animation simulates a sequence of steps the lemming makes in the level from the above example, and makes use of the string representation that should also be displayed by the built-in function print. We also have made explicit animations of the lemming falling down until it hits solid ground, but it should be taken into account that these movements are not separate steps of the simulation.
Lemmingen — een soort woelmuizen — staan erom bekend dat de grootte van hun populatie van jaar tot jaar zeer sterk kan fluctueren. Wanneer er overbevolking van lemmingen optreedt in een bepaald gebied, dan trekken de dieren vaak in groep weg. Deze massale trek spreekt zo tot de verbeelding dat er allerlei volksverhalen over zijn ontstaan. Zo zou de trek niet te stoppen zijn (het dier zou zelfmoord plegen om plaats te maken voor andere lemmingen), en zelfs geen halt houden voor de zee (waarin de dieren massaal zouden verdrinken) of onneembare obstakels (waarvoor de dieren zelfs spontaan zouden exploderen).
Deze volksverhalen werden verder gevoed door de Disney natuurfilm White Wilderness uit 1958, waarin duidelijk te zien is hoe lemmingen in grote getale over een klif vallen. Disney sleepte voor deze natuurfilm zelfs een Academy Award for Best Documentary Feature in de wacht. In de documentaire Cruel Camera uit 1982 werd echter onthuld dat de originele documentaire niet werd gefilmd in Antarctica, maar dat de lemmingen werden overgevlogen van Hudson Bay naar Calgary (Alberta, Canada), waar ze niet uit eigen beweging van een klif sprongen maar ervan gejaagd werden door de cameraploeg.
Het verhaal van de lemmingen inspireerde het Schotse softwarebedrijf DMA Design (tegenwoordig bekend als Rockstar North) tot het ontwikkelen van het computerspel Lemmings. Het computerspel werd een absolute monsterhit tijdens de jaren '90. Via een luik in het plafond werden antropomorfe lemmingen in een level gedropt. Daar liepen ze achter elkaar in een lijn, om pas bij een obstakel te keren. De lemmingen liepen zelfs blindelings naar zaken toe die hen konden doden, zoals water, vuur, lava of een hoge val. Een speler kan een lemming één van de acht mogelijke functies toekennen, waaronder klimmen, graven en blokkeren. De bedoeling is om zo veel mogelijk lemmingen naar de uitgang te leiden door er onderweg zo weinig mogelijk te laten sneuvelen. Voor ieder level geldt een minimum overlevingspercentage. Wanneer dit niet gehaald wordt, dan moet het level opnieuw gespeeld worden.
Opgave
Voor deze opgave vragen we je om een vereenvoudigde simulatie te maken van een lemming in een level van het computerspel Lemmings. Een level van het computerspel bestaat uit een aantal cellen die gerangschikt zijn in de vorm van een rechthoek, en wordt omschreven in een tekstbestand. In die omschrijving geven spaties de vrije cellen aan, en worden cellen met een obstakel aangeduid met een hekje (#). Langs de buitenste rand van het level bevinden zich altijd obstakels. Een level kan er bijvoorbeeld als volgt uitzien.
################################# # # # # # # ### # ########### ### # ########### ######## # ########### ############## # #################################
Omdat elk level de vorm van een rechthoek aanneemt, zullen we de posities in de rechthoek aanduiden door de rijen van boven naar onder, en de kolommen van links naar rechts te nummeren vanaf nul. Voor het level dat we als voorbeeld gebruikt hebben, ziet de nummering er als volgt uit.
Als we via een luik in het plafond een lemming in het level droppen in kolom 3, dan valt de lemming naar beneden tot hij op positie $(3, 3)$ vaste grond onder de voeten krijgt. Als de lemming initieel naar links begint te stappen, dan ziet de situatie van het level er op dat moment als volgt uit.
Bij elke stap in de simulatie beweegt de lemming autonoom in een bepaalde richting. Stel dat de lemming zich naar rechts wil bewegen, dan zijn er drie verschillende mogelijkheden die worden geïllustreerd in onderstaande figuur.
We noemen de cel waarin de lemming zich momenteel bevindt de huidige cel. Als de cel rechts van de huidige cel vrij is (situatie links in bovenstaande figuur) dan verplaatst de lemming zich naar die cel. Daarna valt de lemming naar beneden totdat hij vaste grond onder de voeten heeft (indien dit nog niet het geval was). Als er rechts van de huidige cel een obstakel staat maar de cel boven dit obstakel vrij is (situatie midden in bovenstaande figuur), dan beweegt de lemming naar die vrije cel. Als de cellen rechts en rechtsboven de huidige cel beide een obstakel bevatten, dan blijft de lemming in de huidige cel staan maar beweegt de lemming zich vanaf nu naar links. De lemming gedraagt zich analoog indien hij zich in de volgende stap naar links wil bewegen.
Gevraagd wordt om een klasse Lemming te definiëren waarmee een simulatie van een lemming in een bepaald level van het computerspel Lemmings kan gemaakt worden in Python. Deze klasse moeten minstens de volgende methoden ondersteunen:
- Een initialisatiemethode waaraan drie argumenten moeten doorgegeven worden: i) de locatie van een tekstbestand met de omschrijving van het level, ii) de kolom waar de lemming initieel in het level gedropt wordt via een luik in het plafond en iii) de richting waarin de lemming zich initieel beweegt. De richting wordt aangegeven door een kleiner dan teken (<) indien de lemming zich initieel naar links beweegt en met een groter dan teken (>) indien de lemming zich initieel naar rechts beweegt. Na het uitvoeren van de initialisatiemethode moet de lemming altijd vaste grond onder de voeten hebben.
- Een methode positie die een tuple met drie elementen teruggeeft: i) het rijnummer van de cel waar de lemming zich momenteel bevindt, ii) het kolomnummer van de cel waar de lemming zich momenteel bevindt en iii) de richting waarin de lemming zich momenteel beweegt, aangegeven door een kleiner dan of groter dan teken (analoog als bij de initialisatiemethode).
- Een methode stap waarmee één enkele stap van de simulatie van de lemming wordt uitgevoerd. De methode moet een tuple teruggeven met de positie en beweegrichting van de lemming na het uitvoeren van de stap, waarbij het tuple dezelfde vorm aanneemt als bij de methode positie.
- Een methode stappen waaraan een getal $n \in \mathbb{N}$ moet doorgegeven worden. De methode moet $n$ stappen van de simulatie van de lemming uitvoeren, en moet een lijst teruggeven met de posities en beweegrichtingen van de lemming na het uitvoeren van elk van de opeenvolgende stappen. De positie en beweegrichting van de lemming moet weergegeven worden aan de hand van een tuple dat dezelfde vorm aanneemt als bij de methode positie.
Bovendien moet het mogelijk zijn om met de ingebouwde functie print een stringvoorstelling van de huidige positie en richting van de lemming in het level uit te schrijven. In deze stringvoorstelling moet het level op precies dezelfde manier weergegeven worden als die in het gegeven bestand werd voorgesteld. Daarbij moet de positie waar de lemming zich momenteel bevindt worden aangegeven door een kleiner dan teken (<) indien de lemming zich naar links beweegt en met een groter dan teken (>) indien de lemming zich naar rechts beweegt.
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand level.txt zich in de huidige directory bevindt.
>>> lemming = Lemming('level.txt', 3, '<') >>> lemming.positie() (3, 3, '<') >>> print(lemming) ################################# # # # # # # < ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.stap() (3, 2, '<') >>> lemming.stap() (3, 1, '<') >>> lemming.stap() (3, 1, '>') >>> lemming.stap() (3, 2, '>') >>> print(lemming) ################################# # # # # # # > ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.stappen(5) [(3, 3, '>'), (3, 4, '>'), (3, 5, '>'), (3, 6, '>'), (3, 7, '>')] >>> print(lemming) ################################# # # # # # # >### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.stap() (2, 8, '>') >>> print(lemming) ################################# # # # > # # # ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.stap() (2, 9, '>') >>> lemming.stap() (1, 10, '>') >>> print(lemming) ################################# # > # # # # # ### # ########### ### # ########### ######## # ########### ############## # ################################# >>> lemming.stap() (6, 11, '>') >>> print(lemming) ################################# # # # # # # ### # ########### ### # ########### ######## # ###########> ############## # ################################# >>> lemming.stappen(21) [(6, 12, '>'), (5, 13, '>'), (5, 14, '>'), (4, 15, '>'), (4, 16, '>'), (3, 17, '>'), (3, 18, '>'), (3, 19, '>'), (4, 20, '>'), (4, 21, '>'), (4, 22, '>'), (5, 23, '>'), (5, 24, '>'), (5, 25, '>'), (5, 26, '>'), (6, 27, '>'), (6, 28, '>'), (6, 29, '>'), (6, 30, '>'), (6, 31, '>'), (6, 31, '<')] >>> lemming.stappen(21) [(6, 30, '<'), (6, 29, '<'), (6, 28, '<'), (6, 27, '<'), (5, 26, '<'), (5, 25, '<'), (5, 24, '<'), (5, 23, '<'), (4, 22, '<'), (4, 21, '<'), (4, 20, '<'), (3, 19, '<'), (3, 18, '<'), (3, 17, '<'), (4, 16, '<'), (4, 15, '<'), (5, 14, '<'), (5, 13, '<'), (6, 12, '<'), (6, 11, '<'), (6, 11, '>')] >>> print(lemming) ################################# # # # # # # ### # ########### ### # ########### ######## # ###########> ############## # #################################
Onderstaande animatie simuleert een aantal stappen van de lemming in het level uit bovenstaand voorbeeld, en maakt daarbij gebruik van de stringvoorstelling die ook door de ingebouwde functie print moet weergegeven worden. We hebben ook een expliciete animatie gemaakt van de valbewegingen van de lemming, maar deze vormen geen afzonderlijke stappen in de simulatie.
| Added by: | Peter Dawyndt |
| Date: | 2011-07-23 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS