PROG0036 - Runs and groups
Historically, the Rummikub game was played with two sets of cards. Because this required quite some space on the table, modern versions of the game replaced cards by 106 smaller tiles: two sets of tiles that range in value from one to thirteen, in four colors (red, yellow, blue and black), and two joker tiles ($2 \times 13 \times 4 + 2 = 106$).
At the start of the game, the pool of tiles is shuffled together and spread out face down across the table so that the face of the tiles is not revealed to the players. Each player draws and reveals one tile. The player whose tile has the highest number value will start the game. Tiles are returned to the pool, and players in turn collect 14 random tiles and arrange them on their racks. Play then begins with the starting player, and proceeds in a clockwise direction.
For a player's first move, he must play a set with a value of at least 30 points. Point values are taken from the face value of each tile played, with the joker (if played) assuming the value of the tile it is being used in place of. The player may not use other players' tiles to make the initial 30 or more. A player's first move is known as the initial meld. If a player cannot make an initial meld, he must pick up a single tile from the pool and add it to his rack. Play then proceeds to the next player. Game play continues until a player has used all of the tiles in the rack, at which point he should call out "Rummikub" and is declared the winner.
Assignment
In this assignment we represent a tile in the Rummikub game as a string. This string starts with an integer from the range $[1, 13]$ that represents the value of the tile, followed by a single uppercase letter that represents its color: R (red), Y (yellow), B (blue) or K (black). The jokers are not taken into account.
A collection of tiles that is played on the table will be represented as a list, a tuple or a set of tiles. According to the rules of the game, a collection of tiles can only be played if it contains at least three tiles and if all tiles are different. Apart from these two basic conditions, the rules of the game make a distinction between two valid types of collections that can be played on the table: groups and runs.
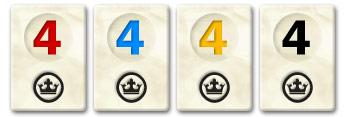
A group of tiles is a collection of tiles that all have the same value but a distinct color. Below, you see an example of a group of four tiles: 4 red, 4 blue, 4 yellow and 4 black.
A run of tiles is a collection of tiles that all have the same color and that can be arranged in such a way that the values form a sequence of consecutive integers. The value 1 does not follow the value 13. Below, you see an example of a run of five tiles: 6 blue, 7 blue, 8 blue, 9 blue and 10 blue.
Your task:
- Write a function group that takes a list, a tuple or a set of tiles. The function must return a Boolean value that indicates whether or not the given tiles are a valid group of tiles.
- Write a function run that takes a list, a tuple or a set of tiles. The function must return a Boolean value that indicates whether or not the given tiles are a valid run of tiles.
Example
>>> group(['4R', '4B', '4Y', '4K']) True >>> group({'6B', '7B', '8B', '9B', '10B'}) False >>> group(('11R', '2B', '7Y', '2B', '9K')) False >>> run(['4R', '4B', '4Y', '4K']) False >>> run({'6B', '7B', '8B', '9B', '10B'}) True >>> run(('11R', '2B', '7Y', '2B', '9K')) False
Rummikub is een gezelschapsspel dat oorspronkelijk werd gespeeld met twee sets kaarten. Omdat daarvoor vrij veel ruimte op de tafel nodig was, zijn de kaarten in moderne versies van het spel vervangen door 106 kleinere stenen: twee sets van de getallen 1 tot en met 13 in de kleuren rood-geel-blauw-zwart en twee jokers ($2 \times 13 \times 4 + 2 = 106$).
Bij aanvang van het spel worden alle stenen op hun kop op tafel gelegd, zodat hun waarde niet zichtbaar is. Deze stenen vormen de pot. Daarna neemt iedere speler 14 stenen uit de pot, en zet ze op zijn rekje. Om te bepalen wie mag beginnen, pakt elke speler een extra steen uit de pot en legt die zichtbaar op tafel. De speler wiens steen de hoogste waarde heeft mag beginnen.
Het doel van het spel is om als eerste al je stenen op tafel te leggen door nieuwe rijtjes en groepen te vormen en open op tafel uit te leggen, of door rijtjes en groepen die open op tafel liggen aan te vullen. Hiervoor moeten de spelers tijdens het spel mogelijks bijkomende stenen uit de pot nemen en op hun rekje plaatsen.
Opgave
In deze opgave stellen we een steen van het spel Rummikub voor als een string. Deze string begint met een natuurlijk getal uit het interval $[1, 13]$ die de waarde van de steen voorstelt, gevolgd door één enkele hoofdletter die de kleur van de steen voorstelt: R (rood), G (geel), B (blauw) of Z (zwart). De jokers worden buiten beschouwing gelaten.
Een reeks stenen die een speler wil uitleggen, zullen we in deze opgave voorstellen als een lijst, een tuple of een verzameling stenen. Volgens de spelregels kan een reeks stenen enkel uitgelegd worden als ze bestaat uit minstens drie stenen en als alle stenen van de reeks verschillend zijn. Naast deze twee basisvoorwaarden wordt er in de spelregels onderscheid gemaakt tussen twee soorten van reeksen stenen die kunnen uitgelegd worden: groepen en rijtjes.
Een groep stenen is een reeks stenen die allemaal dezelfde waarde maar een verschillende kleur hebben. Hieronder zie je bijvoorbeeld een groep van vier stenen: 4 rood, 4 blauw, 4 geel en 4 zwart.
Een rijtje stenen is een reeks stenen die allemaal dezelfde kleur hebben en waarvan de waarden een opeenvolgende rij natuurlijke getallen vormen indien ze in stijgende volgorde geplaatst worden. Hierbij volgt de waarde 1 niet op de waarde 13. Hieronder zie je bijvoorbeeld een rijtje van vijf stenen: 6 blauw, 7 blauw, 8 blauw, 9 blauw en 10 blauw.
Gevraagd wordt:
- Schrijf een functie groep waaraan een lijst, een tuple of een verzameling stenen moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de gegeven stenen een geldige groep stenen vormen.
- Schrijf een functie rijtje waaraan een lijst, een tuple of een verzameling stenen moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de gegeven stenen een geldig rijtje stenen vormen.
Voorbeeld
>>> groep(['4R', '4B', '4G', '4Z']) True >>> groep({'6B', '7B', '8B', '9B', '10B'}) False >>> groep(('11R', '2B', '7G', '2B', '9Z')) False >>> rijtje(['4R', '4B', '4G', '4Z']) False >>> rijtje({'6B', '7B', '8B', '9B', '10B'}) True >>> rijtje(('11R', '2B', '7G', '2B', '9Z')) False
| Added by: | Peter Dawyndt |
| Date: | 2011-07-23 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS