OIA1002 - Changing formation
English version:
The floor of the parade ground of a barracks is gridded with such a spacing that at most one soldier can be positioned in a box. This grid allows numbering rows and columns, placing the 0 in an arbitrary place. It is enough that two adjacent rows or two columns carry consecutive numbers. The existence of this numbering makes it possible to describe rectangles by giving the locations of two squares of the same diagonally opposite. Thus the two vertices (4, 9) and (2, 3) describe a rectangle with 3 rows and 7 columns as illustrated in the figure. (The first coordinate is for the Y-axis, and the second coordinate is for X-axis).
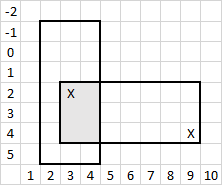
At a certain moment a group of soldiers is arranged in the shape of a rectangle. It is desired that they be regrouped, forming a new rectangle of the same or different dimensions but with the same area.
The general wants to know what is the greatest number of soldiers that could stay in their positions during the regrouping maneuver.
In order to know this result precisely, you are asked to write a program that when given the descriptions of the initial and final rectangles, determines the maximum number of soldiers that can remain stationary during the regrouping maneuver.
Input
The input will be one line for each rectangle. In each line there are 2 pairs of integer numbers. First line for actual formation, second line for final formation. First pair of numbers represents row and column of the cell at a corner of the rectangle, and second pair of numbers represents the diagonal-opposite corner.
The rows and columns numbers are in the range -10000..+10000.
Output
Only one line with the maximum number of soldiers that could be stay in their positions during the maneuver.
Example
Input: 4 9 2 3 -1 4 5 2 Output: 6
Versión en español:
El piso de la plaza de armas de un cuartel está cuadriculado con un espaciado tal que en un casillero se puede posicionar a lo más un soldado. Este cuadriculado permite numerar filas y columnas, colocando el 0 en un lugar arbitrario. Basta con que dos filas o dos columnas adyacentes lleven números consecutivos. La existencia de esta numeración permite describir rec-tángulos dando las ubicaciones de dos casillas del mismo diagonalmente opuestas. Así los dos vértices (4;9) y (2;3) describen un rectángulo de 3 filas y 7 columnas tal como ilustra la figura adjunta.

En determinado momento un grupo de soldados está dispuesto en forma de un rectángulo. Se desea que se reagrupen formando un nuevo rectángulo de iguales o distintas dimensiones pero de la misma superficie.
Se desea saber cuál es la mayor cantidad de soldados que podrían quedarse quietos durante la maniobra de reagrupación.
Para poder conocer con precisión este resultado, se te pide que escribas un programa maniobra.pas, maniobra.c o maniobra.cpp que, dadas las descrip-ciones de los rectángulos inicial y final determine la máxima cantidad de soldados que pueden quedarse quietos durante la maniobra de reagrupación.
Input
Se reciben 2 pares de números enteros en dos líneas. Cada línea representa un rectángulo. El primero describe la formación actual, el segundo la final.
El primer par de números representa fila y columna de una casilla ubicada en un rincón del rectángulo y el segundo para la de otra diagonalmente opuesta.
Los números de filas y columnas están en el rango -10000 a +10000.
Output
Contiene una única línea con un entero indicando la cantidad de soldados que podrían quedarse inmóviles durante la maniobra de reagrupación.
Ejemplo
Input: 4 9 2 3 -1 4 5 2 Output: 6
| Added by: | Coach UTN FRSF |
| Date: | 2013-06-01 |
| Time limit: | 1s-5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | oia.org.ar 2012 |

 RSS
RSS