MGCSCLS - Bob and magical scale
Small Bob received scales with magical bricks. They are magical because they can have minus weight.
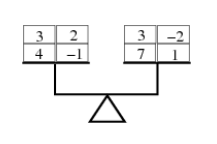
His mom made L towers on the left arm and P towers on the right arm of the scale. Every tower is made with exactly N bricks.
She asked him how many brick he has to put off from each arm to balance the scale. Obviously Bob can only take bricks from top of the tower and he can't put back bricks he has previously taken off. It's too difficult for him. Can you help him solve it in minimum number of moves?
Input
In first line number N, L, P. Number of bricks in every tower. Number of towers on left arm and Number of towers on right arm.
In next L lines: construction of towers on the left arm.
In next P lines: construction of towers on the right arm. (Look at picture below.)
N ≤ 50
L ≤ 25
P ≤ 25
-50 ≤ weight of every brick ≤ 50
Output
Minimal number of moves to balance the scale.
Example
Input: 2 2 2 4 3 -1 2 7 3 1 -2 Output: 2
I made time limit so high because I want all correct solutions to get accepted, but not n! solution.
hide comments
|
|
kshubham02:
2017-04-26 21:56:36
O(n^2 * (l+p)^2) gives TLE (maybe rightly so)
|
|
|
Shashank Yadav:
2014-12-14 19:41:02
//m getting correct ans for the given test case & problem setter's tc yet wa
|
|
|
Krzysztof Lewko:
2011-09-13 14:52:16
You fail on this case:http://pastebin.com/dQy56U1H
|
|
|
sandeep reddy biddala:
2011-09-13 14:52:16
I am getting wa. Could anyone please give me a test case for which it fails. |
|
|
Krzysztof Lewko:
2011-09-13 14:52:16
Yes they can |
|
|
.:: Pratik ::.:
2011-09-13 14:52:16
In the final solution, can the weights on both sides be negative? |
| Added by: | Krzysztof Lewko |
| Date: | 2011-07-01 |
| Time limit: | 1s-1.329s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | III POIG |

 RSS
RSS