MAFBOI08 - Mafia
The police in Byteland got an anonymous tip that the local mafia bosses are planning a big transport from the harbour to one of the secret warehouses in the countryside. The police knows the date of the transport and they know that the transport will use the national highway network.
The highway network consists of two-way highway segments, each segment directly connecting two distinct toll stations. A toll station may be connected with many other stations. A vehicle can enter or exit the highway network at toll stations only. The mafia transport is known to enter the highways at the toll station closest to the harbour and leave it at the toll station closest to the warehouse (it will not leave and re-enter the highways in between). Special police squads are to be located in selected toll stations. When the transport enters a toll station under surveillance, it will be caught by the police.
From this point of view, the easiest choice would be to place the police squad either at the entry point or the exit point of the transport. However, controlling each toll station has a certain cost, which may vary from station to station. The police wants to keep the overall cost as low as possible, so they need to identify a minimal controlling set of toll stations, which satisfies the two conditions:
- all traffic from the harbour to the warehouse must pass through at least one station from that set,
- the cost of monitoring these stations (i.e. the sum of their individual monitoring costs) is minimal.
You may assume that it is possible to get from the harbour to the warehouse using the highways.
Input
The first line of the standard input contains two integers n and m (2 ≤ n ≤ 200, 1 ≤ m ≤ 20000) - the number of toll stations and the number of direct highway segments. The toll stations are numbered from 1 to n.
The second line contains two integers a and b (1 ≤ a, b ≤ n, a ≤ b) - the numbers of the toll stations closest to the harbour and to the warehouse, respectively.
The following n lines describe the monitoring costs. The i-th of these lines (for 1 ≤ i ≤ n) contains one integer - the monitoring cost of the i-th station (which is positive number not exceeding 10000000).
The following m lines describe the highway network. The j-th of these lines (for 1 ≤ j ≤ m) contains two integers x and y (1 ≤ x < y ≤ n), indicating that there is a direct highway segment between toll stations numbered xand y. Each highway segment is listed once.
Output
The only line of the output should contain the numbers of toll stations in a minimal controlling set, given in increasing order, separated by single spaces. If there is more than one minimal controlling set, your program may output anyone of them.
Example
For the input data:
5 6 5 3 2 4 8 3 10 1 5 1 2 2 4 4 5 2 3 3 4
the correct result is:
1 4
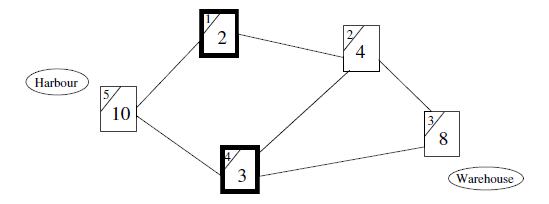
The figure shows the highway network with the toll station numbers (in the upper-left corners) and the monitoring costs. Stations number 1 and 4 constitute the minimal controlling set with total controlling cost 5.
| Added by: | Krzysztof Lewko |
| Date: | 2011-07-23 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | boi 08 |

 RSS
RSS