IOIBOUND - Boundary 2003
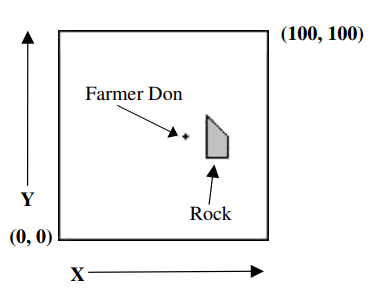
Farmer Don watches the fence that surrounds his N meter by N meter square, flat field (2 ≤ N ≤ 500,000). One fence corner is at the origin (0, 0) and the opposite corner is at (N,N); the sides of Farmer Don's fence are parallel to the X and Y axes. Fence posts appear at all four corners and also at every meter along each side of the fence, for a total of 4×N fence posts. The fence posts are vertical and are considered to have no radius. Farmer Don wants to determine how many of his fence posts he can watch when he stands at a given location within his fence. Farmer Don’s field contains R (1 ≤ R ≤ 30,000) huge rocks that obscure his view of some fence posts, as he is not tall enough to look over any of these rocks. The base of each rock is a convex polygon with nonzero area whose vertices are at integer coordinates. The rocks stand completely vertical. Rocks do not overlap, do not touch other rocks, and do not touch Farmer Don or the fence. Farmer Don does not touch the fence, does not stand within a rock, and does not stand on a rock. Given the size of Farmer Don's fence, the locations and shapes of the rocks within it, and the location where Farmer Don stands, compute the number of fence posts that Farmer Don can see. If a vertex of a rock lines up perfectly with a fence post from Farmer Don's location, he is not able to see that fence post.
Input
The first line of input contains two space-separated integers: N and R. The next line of input contains two space-separated integers that specify the X and Y coordinates of Farmer Don's location inside the fence. The rest of the input file describes the R rocks: Rock i’s description starts with a line containing a single integer pi (3 ≤ pi ≤ 20), the number of vertices in the rock's base. Each of the next pi lines contains a space-separated pair of integers that are the X and Y coordinates of a vertex. The vertices of a rock’s base are distinct and given in counterclockwise order.
Output
The output file should contain a single line with a single integer, the number of fence posts visible to Farmer Don.
Example
Input: 100 1 60 50 5 70 40 75 40 80 40 80 50 70 60 Output: 319
hide comments
|
|
David:
2021-03-26 19:23:41
4N is correct. Each side is from 0 to N. Length is therefore N+1. Two opposite sides have 2(N+1) poles (this accounts for all 4 corner poles). The remaining two sides have 2(N-1) uncounted poles. Total = 2(N+1) + 2(N-1) = 2N + 2 + 2N - 2 = 4N. |
|
|
Valentin Dominte:
2013-10-24 16:11:21
a total of 4×N fence posts? what about the corner posts? if the 4 corner posts are common for 2 sides the total should be 4xN-4 (and the output for the given example 315) Last edit: 2013-10-24 16:12:04 |
| Added by: | Gareev |
| Date: | 2010-08-16 |
| Time limit: | 0.100s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS OBJC PERL6 VB.NET |
| Resource: | IOI 2003, Day 2 |

 RSS
RSS