EE4371 - ISOMORPH
Introduction
Definition: An isomorphism from a simple graph G to a simple graph H is a bijection f:V(G) → V(H) such that uv belongs to E(G) if and only if f(u)f(v) belongs to E(H) . We say “G is isomorphic to H”, if there is an isomorphism from G to H.Example : The following two graphs are isomorphic.
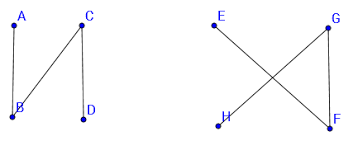
G1 G2
Our objective in this problem is to find isomorphic graphs.
Input
Input is read from STDIN. Each test case consists of graphs all with same number of vertices. Your task in this assignment will be to divide the given set of graphs into classes within which graphs are pairwise isomorphic.
k v [k is the number of graphs (≤ 20) in the test case and v is the number of vertices (≤ 20) in each of these graphs]
e1 [number of edges in first graph, call this graph ‘1’]
u1 w1
u2 w2
...
ue1 we1
e2 [number of edges in second graph, call this graph ‘2’]
u1 w1
u2 w2
...
ue2 we2
e3
...
...
...
ek [number of edges in the last graph, call this graph ‘k’]
u1 w1
u2 w2
...
uek wek
[Note: all n graphs themselves are named ‘1’, ‘2’...’n’ in the order in which they appear in the input. Hence the graph with e1 edges is called ‘1’ and so on]
[Note: all graphs are simple & undirected; vertices are labelled with numbers, not alphabets.]
Output
An isomorphic class is simply a list of graphs which belong to it. And Output is written to STDOUT.
The output should follow the below format:
1. Output is a listing of all isomorphic classes, one on each line, sorted in ascending order by the first
graph of the class.
2. Within an isomorphic class, the members are printed in ascending order.
(Thus, the class containing graph ‘1’ is always on line 1.)
hide comments
|
|
Jacob Plachta:
2015-12-22 14:51:23
Something's wrong with the data - the values for u and w range between 0 and v, inclusive. I'm guessing that some graphs' nodes are 0-indexed while others are 1-indexed, or something.
|
| Added by: | Saketh BSV |
| Date: | 2015-03-25 |
| Time limit: | 1s-10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | MAWK BC C-CLANG C NCSHARP C++ 4.3.2 CPP CPP14 CPP14-CLANG COFFEE D-CLANG D-DMD DART ELIXIR FANTOM FORTH JAVA JULIA KTLN NIM OBJC OBJC-CLANG OCT PICO PROLOG PYTHON PYPY3 PYTHON3 PY_NBC R RACKET RUST CHICKEN SQLITE SWIFT UNLAMBDA |

 RSS
RSS