AE5A1 - Circular game
| English | Vietnamese |
Cho một bàn cờ gồm m ô được xếp thành một vòng tròn, đánh số từ 1 đến m. Trên bàn cờ có b quân cờ trắng và c quân cờ đen, có tối đa 1 quân cờ trong 1 ô. Hai người chơi trò chơi này như sau: Người cầm quân trắng bắt đầu trước, 2 người lần lượt thực hiện nước đi của mình. Mỗi nước đi, người chơi được quyền di chuyển quân cờ của mình tiến lên hoặc lùi đi một số ô trống. Ví dụ, trong hình vẽ dưới đây, người chơi cầm quân trắng có thể di chuyển quân từ ô 3 đến ô 4, hoặc quân từ ô 8 đến một trong các ô 7, 9, và 1.
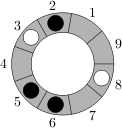
Người chơi nào không thể thực hiện được nước đi của mình là người thua cuộc. Gỉả sử cả 2 người đề chơi tối ưu, hỏi ai là người chiến thắng? Có thể xảy ra trường hợp không có ai thắng (trò chơi không bao giờ kết thúc).
Input
Dòng đầu chứa số nguyên t là số lượng bộ test.
Các dòng tiếp theo mô tả lần lượt t bộ test, mỗi bộ gồm 3 dòng. Dòng đầu tiên chứa 3 số nguyên m, b và c (1 ≤ m ≤ 109, 1 ≤ b, c) thể hiện độ dài của bàn cờ, số lượng quân trắng, và số lượng quân đen. Dòng thứ hai chứa một dãy số tăng dần gồm b số nguyên (trong khoảng 1 ... m) thể hiện vị trí của các quân cờ trắng. Dòng thứ 3 chứa một dãy số tăng dần gồm c số nguyên (trong khoảng 1 ... m) thể hiện vị trí của các quân cờ đen. Tổng số quân cờ trên bàn cờ không vượt quá 106.
Output
Gồm đúng t dòng, ghi kết quả của t test. Kết quả là một trong số 3 loại kí tự: B, C, hoặc R, tuỳ thuộc vào việc người cầm quân trắng thắng (B), người cầm quân đen thắng (C) hay trò chơi không bao giờ kết thúc (R).
Example
Với dữ liệu:
3 9 2 3 3 8 2 5 6 6 2 2 5 6 2 4 7 1 1 3 4
Kết quả đúng là:
C B R
| Added by: | Race with time |
| Date: | 2009-05-03 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO PERL6 |
| Resource: | Algorithmic Engagements 2009 |

 RSS
RSS