The company Flauta wants to introduce a new package containing one kg of bread (which curiously shall be sliced bread). As part of the package design team, you have been tasked with designing a nutritional pyramid in accordance to the company's requirements. The nutritional pyramid will be represented by a triangular grid of side L, which is an equilateral triangle divided in unitary triangles (i.e. equilateral triangles of side one) by drawing lines parallel to the sides of the bigger triangle. For example, in the following figure you can see triangular grids for L = 4, 5 and 6.
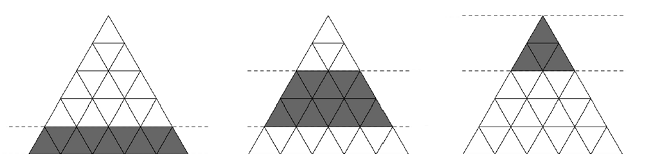
There are K different types of food to be shown on the nutritional pyramid, and each of them will be represented by a horizontal section of the grid. A horizontal section is that part of the pyramid that lies between two lines parallel to the base of the grid, drawn in such a way that they only touch the unitary triangles at their borders, without crossing them. In the following figure three valid horizontal sections can be seen shaded in a grid with L = 5.
It is important for the K sections in which the nutritional pyramid is divided to be easily seen, and for this reason each of them should be composed of many unitary triangles. However, because the size of the grid is fixed there is a limited number of unitary triangles to distribute among all K sections. To make sure that no section is left disproportionately small, you have been asked to find out the maximum number of unitary triangles that can make up the smallest section of the pyramid, if the sections are chosen optimally.
For example, in the following figure three different ways to divide a grid of side L = 5 in K = 3 are represented.

The grid on the left has two sections with 9 unitary triangles each, having the other section 7 unitary triangles. In the central grid, the sections have 12, 9 and 4 unitary triangles, whereas in the grid on the right they have 16, 8 and 1. Of these three choices, the best one is then represented by the grid on the left, for it has 7 unitary triangles in its smallest section, while the central grid has 4 unitary triangles and the grid on the right has only 1 such triangle. In fact, the choice of sections represented in the grid on the left of the figure is optimal, as there is no other possible choice of K = 3 horizontal sections in which the smallest of them has more than 7 unitary triangles.
The company Flauta wants to introduce a new package containing one kg of bread (which curiously shall be sliced bread). As part of the package design team, you have been tasked with designing a nutritional pyramid in accordance to the company's requirements. The nutritional pyramid will be represented by a triangular grid of side L, which is an equilateral triangle divided in unitary triangles (i.e. equilateral triangles of side one) by drawing lines parallel to the sides of the bigger triangle. For example, in the following figure you can see triangular grids for L = 4, 5 and 6.
There are K different types of food to be shown on the nutritional pyramid, and each of them will be represented by a horizontal section of the grid. A horizontal section is that part of the pyramid that lies between two lines parallel to the base of the grid, drawn in such a way that they only touch the unitary triangles at their borders, without crossing them. In the following figure three valid horizontal sections can be seen shaded in a grid with L = 5.
It is important for the K sections in which the nutritional pyramid is divided to be easily seen, and for this reason each of them should be composed of many unitary triangles. However, because the size of the grid is fixed there is a limited number of unitary triangles to distribute among all K sections. To make sure that no section is left disproportionately small, you have been asked to find out the maximum number of unitary triangles that can make up the smallest section of the pyramid, if the sections are chosen optimally.
For example, in the following figure three different ways to divide a grid of side L = 5 in K = 3 are represented.
The grid on the left has two sections with 9 unitary triangles each, having the other section 7 unitary triangles. In the central grid, the sections have 12, 9 and 4 unitary triangles, whereas in the grid on the right they have 16, 8 and 1. Of these three choices, the best one is then represented by the grid on the left, for it has 7 unitary triangles in its smallest section, while the central grid has 4 unitary triangles and the grid on the right has only 1 such triangle. InThe company Flauta wants to introduce a new package containing one kg of bread (which curiously shall be sliced bread). As part of the package design team, you have been tasked with designing a nutritional pyramid in accordance to the company's requirements. The nutritional pyramid will be represented by a triangular grid of side L, which is an equilateral triangle divided in unitary triangles (i.e. equilateral triangles of side one) by drawing lines parallel to the sides of the bigger triangle. For example, in the following figure you can see triangular grids for L = 4, 5 and 6.
There are K different types of food to be shown on the nutritional pyramid, and each of them will be represented by a horizontal section of the grid. A horizontal section is that part of the pyramid that lies between two lines parallel to the base of the grid, drawn in such a way that they only touch the unitary triangles at their borders, without crossing them. In the following figure three valid horizontal sections can be seen shaded in a grid with L = 5.
It is important for the K sections in which the nutritional pyramid is divided to be easily seen, and for this reason each of them should be composed of many unitary triangles. However, because the size of the grid is fixed there is a limited number of unitary triangles to distribute among all K sections. To make sure that no section is left disproportionately small, you have been asked to find out the maximum number of unitary triangles that can make up the smallest section of the pyramid, if the sections are chosen optimally.
For example, in the following figure three different ways to divide a grid of side L = 5 in K = 3 are represented.
The grid on the left has two sections with 9 unitary triangles each, having the other section 7 unitary triangles. In the central grid, the sections have 12, 9 and 4 unitary triangles, whereas in the grid on the right they have 16, 8 and 1. Of these three choices, the best one is then represented by the grid on the left, for it has 7 unitary triangles in its smallest section, while the central grid has 4 unitary triangles and the grid on the right has only 1 such triangle. In fact, the choice of sections represented in the grid on the left of the figure is optimal, as there is no other possible choice of K = 3 horizontal sections in which the smallest of them has more than 7 unitary triangles.The company Flauta wants to introduce a new package containing one kg of bread (which curiously shall be sliced bread). As part of the package design team, you have been tasked with designing a nutritional pyramid in accordance to the company's requirements. The nutritional pyramid will be represented by a triangular grid of side L, which is an equilateral triangle divided in unitary triangles (i.e. equilateral triangles of side one) by drawing lines parallel to the sides of the bigger triangle. For example, in the following figure you can see triangular grids for L = 4, 5 and 6.
There are K different types of food to be shown on the nutritional pyramid, and each of them will be represented by a horizontal section of the grid. A horizontal section is that part of the pyramid that lies between two lines parallel to the base of the grid, drawn in such a way that they only touch the unitary triangles at their borders, without crossing them. In the following figure three valid horizontal sections can be seen shaded in a grid with L = 5.
It is important for the K sections in which the nutritional pyramid is divided to be easily seen, and for this reason each of them should be composed of many unitary triangles. However, because the size of the grid is fixed there is a limited number of unitary triangles to distribute among all K sections. To make sure that no section is left disproportionately small, you have been asked to find out the maximum number of unitary triangles that can make up the smallest section of the pyramid, if the sections are chosen optimally.
For example, in the following figure three different ways to divide a grid of side L = 5 in K = 3 are represented.
The grid on the left has two sections with 9 unitary triangles each, having the other section 7 unitary triangles. In the central grid, the sections have 12, 9 and 4 unitary triangles, whereas in the grid on the right they have 16, 8 and 1. Of these three choices, the best one is then represented by the grid on the left, for it has 7 unitary triangles in its smallest section, while the central grid has 4 unitary triangles and the grid on the right has only 1 such triangle. In fact, the choice of sections represented in the grid on the left of the figure is optimal, as there is no other possible choice of K = 3 horizontal sections in which the smallest of them has more than 7 unitary triangles.
Input
There are multiple test cases in the input file. Each test case consists of one line containing two integers L and K, respectively representing the length of the side of the triangular grid and the number of sections in which said grid is to be divided (1 ≤ K ≤ L ≤ 106).
Output
For each test case, print one line containing an integer representing the maximum number of unitary triangles that can make up the smallest horizontal section.
Example
Input:
5 3
5 2
1000000 1
1000000 30000
Output:
7
9
1000000000000
32679639





 RSS
RSS