| Submit | All submissions | Best solutions | Back to list |
RELATS1 - Relations |
You are given a directed graph, whose edges are labeled with relational symbols '<', '>' and '='. For a nonnegative integer k, a k-correct G-labeling is a mapping from vertices of G into integers from interval [0,k] such that numbers at the ends of each edge satisfy the relation described by the label of the edge. We assume that an element on the left side of the relational symbol is a number assigned to the initial vertex. Compute the smallest k for which k-correct G-labeling exists or verify that such labeling doesn't exist for any k.
Illustration
For the graph in the figure the smallest k = 2.
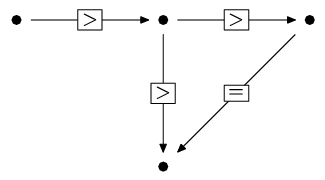
Task
Write a program that for each data set from a sequence of several data sets:
- reads a description of a graph G from the input file,
- verifies whether there exist an integer k for which it is possible to label G k-correctly and, if the answer is positive, computes the smallest such k,
- writes the result to the output file.
Input
The first line of the input file contains one positive integer d not larger than 10. This is the number of data sets. The data sets follow. Each data set is described in two consecutive lines of the input file. In the first line there are two integers n and m separated by a single space. The number n is the number of vertices of G and m is the number of edges of G. Numbers n and m satisfy the inequalities: 1 <= n <= 1000, 0 <= m <= 10000. The vertices are numbered with integers from 1 to n and are identified by these numbers. There are no parallel edges and self-loops in the graph. (Two different edges u1 -> v1 and u2 -> v2 are parallel iff u1 = u2 and v1 = v2.) There are 3m integers separated by single spaces in the second line. The numbers at positions 3i-2 and 3i-1, 1 <= i <= m, are the ends of the i-th edge, the beginning and the end, respectively, whereas the number at position 3i is a number from the set {-1,0,1} and it is the label of the i-th edge: -1 represents '<', 0 represents '=' and 1 represents '>'.
Output
For the i-th data set, 1 <= i <= d, your program should write one word NO in the i-th line of the output file if a k-correct labeling doesn't exist for any k, or the smallest integer k for which such a labeling exists.
Example
Sample input: 4 4 4 1 2 -1 2 3 0 2 4 -1 3 4 -1 2 2 1 2 -1 2 1 -1 2 2 1 2 -1 2 1 1 3 3 1 2 0 3 2 0 3 1 0 Sample output: 2 NO 1 0
| Added by: | adrian |
| Date: | 2004-06-08 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | III Polish Collegiate Team Programming Contest (AMPPZ), 1998 |
hide comments
|
2021-05-28 01:28:43
I have some cases (each are an individual input) 1 6 6 1 2 -1 2 3 -1 3 4 -1 5 6 -1 6 4 -1 3 5 0 1 6 7 1 2 -1 2 3 -1 3 4 -1 5 6 -1 6 4 -1 3 5 0 3 5 1 1 6 7 1 2 -1 2 3 -1 3 4 -1 5 6 -1 6 4 -1 3 5 0 2 3 1 Also make sure in a group of equal vertices there's no other > or < edges among them |
|
|
2013-11-01 13:33:04 Sebastian
Could someone give me some tricky input? I 'm trying everything I can and still getting WA |
|
|
2010-07-29 03:34:53 Bittu Sarkar
is the graph guaranteed to be connected? |


 RSS
RSS