| Submit | All submissions | Best solutions | Back to list |
PROG0600 - Diffy |
The diffy game is great for practicing subtraction, but it also requires students to think logically and identify patterns. It can be played with integers, fractions, decimals and money, but most often it is played with natural numbers.
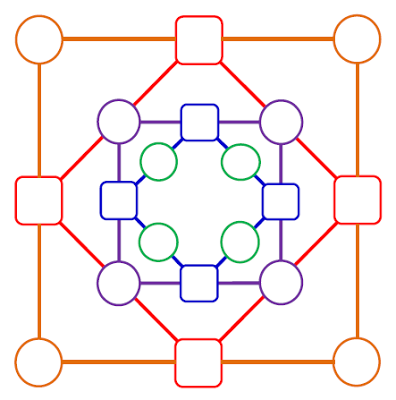
The game begins by writing four random numbers into the four circles on each of the outer corners. Then, the outer squares are filled in by subtracting the smaller number from the larger number on each neighbouring corner. This procedure in which neighbouring corners are subtracted is repeated towards the center. What patterns do you observe? Can you get to the center without any zero differences?
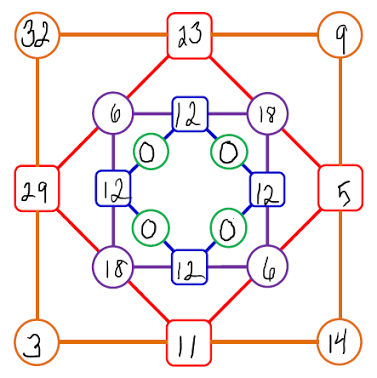
The above figure shows a completed example of a diffy game. As you can see, the player did not win because the circles closest to the center all came up zero. Is it possible to win this game?
Assignment
The diffy game is a special case of a Ducci sequence, named after the Italian mathematician Enrico Ducci who is credited with the discovery of this sequence of $n$-tuples of integers. Given an $n$-tuple of integers $(a_1, a_2, \ldots, a_n)$, the next $n$-tuple in the sequence is formed by taking the absolute differences of neighbouring integers: $$(a_1, a_2, \ldots, a_n) \rightarrow (|a_1 - a_2|, |a_2 - a_3|, \ldots, |a_{n - 1} - a_n|, |a_n - a_1|)$$ This procedure assumes that the last integer in the $n$-tuple is followed by the first integer. Another way of describing the progression of the sequence is as follows. Arrange $n$ integers in a circle and make a new circle by taking the difference between neighbours, ignoring minus signs. Then repeat the operation.
Because every Ducci sequence of integers eventually will repeat itself (a property that is easily proven), Ducci sequences are periodic. Each Ducci sequence will eventually reach an $n$-tuple of zeros (in this case the period is equal to zero), or an $n$-tuple that previously occurred in the Ducci sequence (in this case the period equals the number of $n$-tuples before repetition occurs). For example, consider the following Ducci sequence: $$\begin{matrix} (1, 2, 1, 2, 1, 1) & \rightarrow & \mathbf{(1, 1, 1, 1, 0, 0)} & \rightarrow & \mathbf{(0, 0, 0, 1, 0, 1)} & \rightarrow \\ \mathbf{(0, 0, 1, 1, 1, 1)} & \rightarrow & \mathbf{(0, 1, 0, 0, 0, 1)} & \rightarrow & \mathbf{(1, 1, 0, 0, 1, 1)} & \rightarrow \\ \mathbf{(0, 1, 0, 1, 0, 0)} & \rightarrow & (1, 1, 1, 1, 0, 0) & \rightarrow & \cdots & \\ \end{matrix}$$ The first repetition occurs when the tuple $(1, 1, 1, 1, 0, 0)$ pops up in the sequence a second time. To make this clear, we have highlighted all tuples that are part of the first period using bold face text. The period of this Ducci sequence may thus be determined by counting the number of steps needed to progress from the first occurrence of the tuple $(1, 1, 1, 1, 0, 0)$ to the second occurrence of this tuple. In this case, the period is equal to six. Your task:
- Write a function next that takes a list or a tuple of $n \in \mathbb{N}_0$ integers. The function must return the $n$-tuple of integers that follows the given list or tuple in a Ducci sequence.
- Write a function ducci that takes a list or a tuple of $n \in \mathbb{N}_0$ integers. The function must return the Ducci sequence (represented by a tuple) that starts with the given $n$-tuple, and continues repeatedly with the next $n$-tuple in the Ducci sequence. The sequence either ends in the first $n$-tuple of zeros or the first $n$-tuple that occurs twice in the Ducci sequence.
- Write a function period that takes a list or a tuple of $n \in \mathbb{N}_0$ integers. The function must return the period of the Ducci sequence that starts with the given $n$-tuple.
Example
>>> next([32, 9, 14, 3]) (23, 5, 11, 29) >>> next((1, 2, 1, 2, 1, 0)) (1, 1, 1, 1, 1, 1) >>> next((1, 2, 1, 2, 1, 1)) (1, 1, 1, 1, 0, 0) >>> ducci([32, 9, 14, 3]) ((32, 9, 14, 3), (23, 5, 11, 29), (18, 6, 18, 6), (12, 12, 12, 12), (0, 0, 0, 0)) >>> ducci((1, 2, 1, 2, 1, 0)) ((1, 2, 1, 2, 1, 0), (1, 1, 1, 1, 1, 1), (0, 0, 0, 0, 0, 0)) >>> ducci((1, 2, 1, 2, 1, 1)) ((1, 2, 1, 2, 1, 1), (1, 1, 1, 1, 0, 0), (0, 0, 0, 1, 0, 1), (0, 0, 1, 1, 1, 1), (0, 1, 0, 0, 0, 1), (1, 1, 0, 0, 1, 1), (0, 1, 0, 1, 0, 0), (1, 1, 1, 1, 0, 0)) >>> period([32, 9, 14, 3]) 0 >>> period((1, 2, 1, 2, 1, 0)) 0 >>> period((1, 2, 1, 2, 1, 1)) 6
Het rekenspelletje diffy wordt gebruikt om kinderen te leren aftrekken, en hen tegelijkertijd te leren om logisch na te denken en patronen te herkennen. Het kan gespeeld worden met gehele getallen, breuken, reële getallen en geldbedragen, maar meestal wordt gewerkt met natuurlijke getallen.
Het spelletje begint met het invullen van vier willekeurige getallen in de vier cirkels op de buitenste hoekpunten. Daarna moeten de buitenste vierkanten ingevuld worden door telkens het kleinste getal af te trekken van het grootste getal op de twee naburige hoekpunten. Deze procedure waarbij naburige hoekpunten van elkaar afgetrokken worden en steeds naar binnen toe gewerkt wordt, moet telkens herhaald worden. Zie je een bepaald patroon ontstaan? Kan je het midden bereiken zonder een verschil te krijgen dat nul oplevert?
Hierboven staat een volledig ingevuld voorbeeld van een spelletje diffy. Zoals je kan zien is de speler niet gewonnen, omdat de vier cirkels die het dichtst bij het centrum gelegen zijn allemaal nullen bevatten. Is het überhaupt mogelijk om dit spelletje te winnen?
Opgave
Het spelletje diffy is een speciaal geval van een Ducci-reeks, vernoemd naar de Italiaanse wiskundige Enrico Ducci aan wie de ontdekking van de reeks wordt toegeschreven. Voor een gegeven reeks van $n$ natuurlijke getallen $(a_1, a_2, \ldots, a_n)$ wordt de volgende reeks van $n$ getallen gevormd door de absolute waarde te nemen van het verschil van de opeenvolgende getallen: $$(a_1, a_2, \ldots, a_n) \rightarrow (|a_1 - a_2|, |a_2 - a_3|, \ldots, |a_{n - 1} - a_n|, |a_n - a_1|)$$ Hierbij wordt dus verondersteld dat het laatste getal terug gevolgd wordt door het eerste getal. De Ducci-reeks kan dus ook als volgt omschreven worden. Plaats $n$ natuurlijke getallen op een cirkel en maak een nieuwe cirkel door het verschil van elke twee naburige getallen te bepalen, waarbij het teken genegeerd wordt. Blijf deze procedure herhalen.
Omdat elke Ducci-reeks van natuurlijke getallen uiteindelijk zichzelf zal herhalen (een eigenschap die makkelijk kan bewezen worden), wordt gezegd dat Ducci-reeksen periodiek zijn. Een Ducci-reeks levert uiteindelijk immers een reeks van $n$ natuurlijke getallen op die allemaal nul zijn (periode is gelijk aan 0), of een reeks van $n$ natuurlijke getallen die reeds eerder in de Ducci-reeks voorkwam (periode is gelijk aan het aantal reeksen van $n$ natuurlijke getallen waarna terug herhaling optreedt). Beschouw bijvoorbeeld de volgende Ducci-reeks: $$\begin{matrix} (1, 2, 1, 2, 1, 1) & \rightarrow & \mathbf{(1, 1, 1, 1, 0, 0)} & \rightarrow & \mathbf{(0, 0, 0, 1, 0, 1)} & \rightarrow \\ \mathbf{(0, 0, 1, 1, 1, 1)} & \rightarrow & \mathbf{(0, 1, 0, 0, 0, 1)} & \rightarrow & \mathbf{(1, 1, 0, 0, 1, 1)} & \rightarrow \\ \mathbf{(0, 1, 0, 1, 0, 0)} & \rightarrow & (1, 1, 1, 1, 0, 0) & \rightarrow & \cdots & \\ \end{matrix}$$ De eerste herhaling treedt op als het tuple $(1, 1, 1, 1, 0, 0)$ voor de tweede keer in de reeks opduikt. Om dit te onderstrepen hebben we alle tuples uit de Ducci-reeks die deel uitmaken van de eerste periode in het vet gezet. De periode kan dus bepaald worden als het aantal stappen die nodig zijn om vanaf het eerste voorkomen van het tuple $(1, 1, 1, 1, 0, 0)$ voor het eerst terug het tuple $(1, 1, 1, 1, 0, 0)$ te bekomen. In dit geval is de periode dus gelijk aan zes. Gevraagd wordt:
- Schrijf een functie volgende waaraan een lijst of een tuple van $n \in \mathbb{N}_0$ natuurlijke getallen moet doorgegeven worden. De functie moet het tuple van $n$ natuurlijke getallen teruggeven dat in een Ducci-reeks volgt op de gegeven reeks getallen.
- Schrijf een functie ducci waaraan een lijst of een tuple van $n \in \mathbb{N}_0$ natuurlijke getallen moet doorgegeven worden. De functie moet de reeks teruggeven (voorgesteld door een tuple) die begint bij het tuple dat de gegeven reeks van $n$ natuurlijke getallen voorstelt, en telkens gevolgd wordt door het volgende tuple van $n$ natuurlijke getallen uit de Ducci-reeks. De reeks eindigt wanneer het laatste tuple allemaal nullen bevat of reeds eerder in de Ducci-reeks voorkwam.
- Schrijf een functie periode waaraan een lijst of een tuple van $n \in \mathbb{N}_0$ natuurlijke getallen moet doorgegeven worden. De functie moet de periode van de Ducci-reeks teruggeven die begint met de gegeven reeks van $n$ natuurlijke getallen.
Voorbeeld
>>> volgende([32, 9, 14, 3]) (23, 5, 11, 29) >>> volgende((1, 2, 1, 2, 1, 0)) (1, 1, 1, 1, 1, 1) >>> volgende((1, 2, 1, 2, 1, 1)) (1, 1, 1, 1, 0, 0) >>> ducci([32, 9, 14, 3]) ((32, 9, 14, 3), (23, 5, 11, 29), (18, 6, 18, 6), (12, 12, 12, 12), (0, 0, 0, 0)) >>> ducci((1, 2, 1, 2, 1, 0)) ((1, 2, 1, 2, 1, 0), (1, 1, 1, 1, 1, 1), (0, 0, 0, 0, 0, 0)) >>> ducci((1, 2, 1, 2, 1, 1)) ((1, 2, 1, 2, 1, 1), (1, 1, 1, 1, 0, 0), (0, 0, 0, 1, 0, 1), (0, 0, 1, 1, 1, 1), (0, 1, 0, 0, 0, 1), (1, 1, 0, 0, 1, 1), (0, 1, 0, 1, 0, 0), (1, 1, 1, 1, 0, 0)) >>> periode([32, 9, 14, 3]) 0 >>> periode((1, 2, 1, 2, 1, 0)) 0 >>> periode((1, 2, 1, 2, 1, 1)) 6
| Added by: | Peter Dawyndt |
| Date: | 2015-12-01 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |


 RSS
RSS