SPOJ.com - Problem PROG0595

PROG0595 - Snowball numbers

What's unusual about the number 313,340,350,000,000,000,499? Its English name

THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE

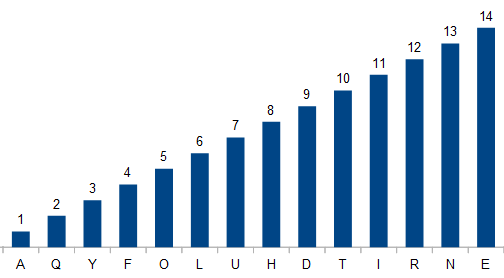
has the following letter count distribution:

The name of the number 313,340,350,000,000,000,499 has a letter count distribution that corresponds to a snowball.

This makes the name a perfect "snowball" in the language of wordplay enthusiasts. In exploring this phenomenon for the November 2012 issue of Word Ways, Eric Harshbarger and Mike Keith found hundreds of thousands of solutions among very large numbers. However, they note the following about the above example:

It is shockingly small compared to all other known snowball histogram numbers (of any order). It seems very likely that this is the smallest snowball histogram number of any order, but a proof of this fact, even with computer assistance, seems difficult.

In the same article, Harshbarger and Keith come up with two other pretty findings. The number 224,000,000,000,525,535, or

TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE

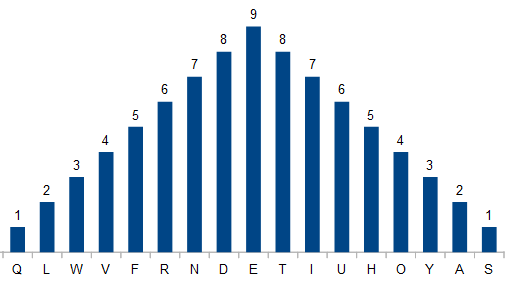
produces a "growing/melting" snowball:

The name of the number 224,000,000,000,525,535 has a letter count distribution that corresponds to a "growing/melting" snowball.

And the number 520,636,000,000,757,000, or

FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND

has a letter count distribution that corresponds to the first 18 digits of the constant $\pi$:

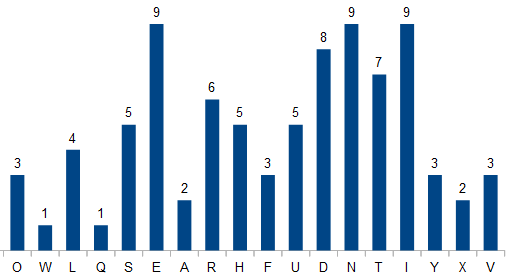
The name of the number 224,000,000,000,525,535 has a letter count distribution that corresponds to the first 18 digits of the constant $\pi$.

At the end of their article they make the following consideration:

This idea can also be applied to arbitrary text, not just number names. Can you find a sentence in Moby Dick or Pride and Prejudice whose letter distribution is a snowball or is interesting in some other way? Such possibilities are left for future consideration.

Assignment

In this assignment, we represent the letter count distribution of a given string as a dictionary that maps all letters that occur in the string onto their number of occurrences in the string. Letter counting is done case insensitive, where the upper case version of the letters are used as keys in the dictionary. Letters that do not occur in the string should not be used as keys in the dictionary. The characters of the string that are not letters should be ignored when determining the letter count distribution. You are asked to:

Write a function letterDistribution that takes a string argument. The function must return a dictionary that represents the letter count distribution of the given string.
Write a function snowball that takes a string argument. The function must return a Boolean value that indicates whether or not the letter count distribution of the given string corresponds to a snowball distribution.
Write a function pyramid that takes a string argument. The function must return a Boolean value that indicates whether or not the letter count distribution of the given string corresponds to a "growing/melting" snowball distribution.
Write a function pi that takes a string argument. The function must return a Boolean value that indicates whether or not the letter count distribution of the given string corresponds to the first digits of the number $\pi$. Before you start looking for an accurate representation of the number $\pi$, here are its first 50 significant digits:

3.1415926535897932384626433832795028841971693993751

Example

>>> letterDistribution('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
{'U': 7, 'I': 11, 'T': 10, 'L': 6, 'O': 5, 'Q': 2, 'N': 13, 'E': 14, 'D': 9, 'A': 1, 'R': 12, 'F': 4, 'H': 8, 'Y': 3}
>>> letterDistribution('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
{'W': 3, 'V': 4, 'U': 6, 'I': 7, 'T': 8, 'A': 2, 'O': 4, 'Q': 1, 'N': 7, 'E': 9, 'D': 8, 'R': 6, 'S': 1, 'F': 5, 'H': 5, 'Y': 3, 'L': 2}
>>> letterDistribution('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
{'W': 1, 'X': 2, 'V': 3, 'U': 5, 'I': 9, 'T': 7, 'A': 2, 'O': 3, 'Q': 1, 'N': 9, 'E': 9, 'D': 8, 'R': 6, 'S': 5, 'F': 3, 'H': 5, 'Y': 3, 'L': 4}

>>> snowball('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
True
>>> snowball('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
False
>>> snowball('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
False

>>> pyramid('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
False
>>> pyramid('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
True
>>> pyramid('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
False

>>> pi('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
False
>>> pi('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
False
>>> pi('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
True

Resources

Harshbarger E, Keith M (2012). Number Names With A Snowball Letter Distribution, Word Ways 45(4), article 10.

Wat is er zo ongebruikelijk aan het getal 313,340,350,000,000,000,499? De Engelse benaming van dit getal

THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE

heeft de volgende verdeling van het aantal voorkomens van de letters:

De naam van het getal 313,340,350,000,000,000,499 heeft een letterverdeling die correspondeert met een sneeuwbal.

Hierdoor wordt de naam van het getal een perfect voorbeeld van een "sneeuwbal" in de terminologie die gebruikt wordt door fanaten van woordspelletjes. In de November 2012 editie van het tijdschrift Word Ways hebben Eric Harshbarger en Mike Keith dit fenomeen nader onderzocht, en hebben daarbij honderdduizenden voorbeelden gevonden tussen de namen van zeer grote getallen. Over het bovenstaande voorbeeld schrijven ze echter:

It is shockingly small compared to all other known snowball histogram numbers (of any order). It seems very likely that this is the smallest snowball histogram number of any order, but a proof of this fact, even with computer assistance, seems difficult.

In datzelfde artikel vermelden Harshbarger en Keith nog twee andere wetenswaardigheden. Het getal 224,000,000,000,525,535, ofte

TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE

resulteert in een "groeiende/smeltende" sneeuwbal:

De naam van het getal 224,000,000,000,525,535 heeft een letterverdeling die correspondeert met een "groeiende/smeltende" sneeuwbal.

Het getal 520,636,000,000,757,000, ofte

FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND

heeft een letterverdeling die overeenkomt met de eerste 18 cijfers van het getal $\pi$:

De naam van het getal 520,636,000,000,757,000 heeft een letterverdeling die correspondeert met de eerste 18 cijfers van het getal $\pi$.

Ze sluiten hun artikel af met de volgende bedenking:

This idea can also be applied to arbitrary text, not just number names. Can you find a sentence in Moby Dick or Pride and Prejudice whose letter distribution is a snowball or is interesting in some other way? Such possibilities are left for future consideration.

Opgave

In deze opgave stellen we de letterverdeling van een gegeven string voor als een dictionary, die alle letters die voorkomen in de string afbeeldt op hun aantal voorkomens in de string. Hierbij wordt geen onderscheid gemaakt tussen hoofdletters en kleine letters, en wordt de hoofdlettervariant van de letters gebruikt als sleutel in de dictionary. Letters die niet voorkomen in de string mogen ook niet als sleutel gebruikt worden in de dictionary. De karakters van de string die geen letters zijn, worden genegeerd bij het bepalen van de letterverdeling. Gevraagd wordt:

Schrijf een functie letterverdeling waaraan een string moet doorgegeven worden. De functie moet een dictionary teruggeven die de letterverdeling van de gegeven string voorstelt.
Schrijf een functie sneeuwbal waaraan een string moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven, die aangeeft of de letterverdeling van de gegeven string overeenkomt met de verdeling van een sneeuwbal.
Schrijf een functie pyramide waaraan een string moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven, die aangeeft of de letterverdeling van de gegeven string overeenkomt met de verdeling van een "groeiende/smeltende" sneeuwbal.
Schrijf een functie pi waaraan een string moet doorgegeven worden. De functie moet een Booleaanse waarde teruggeven, die aangeeft of de letterverdeling van de gegeven string overeenkomt met de eerste cijfers van het getal $\pi$. Voor je zelf begint te zoeken naar een accurate voorstelling van het getal $\pi$, geven we je alvast de eerste 50 significante cijfers:

3.1415926535897932384626433832795028841971693993751

Voorbeeld

>>> letterverdeling('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
{'U': 7, 'I': 11, 'T': 10, 'L': 6, 'O': 5, 'Q': 2, 'N': 13, 'E': 14, 'D': 9, 'A': 1, 'R': 12, 'F': 4, 'H': 8, 'Y': 3}
>>> letterverdeling('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
{'W': 3, 'V': 4, 'U': 6, 'I': 7, 'T': 8, 'A': 2, 'O': 4, 'Q': 1, 'N': 7, 'E': 9, 'D': 8, 'R': 6, 'S': 1, 'F': 5, 'H': 5, 'Y': 3, 'L': 2}
>>> letterverdeling('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
{'W': 1, 'X': 2, 'V': 3, 'U': 5, 'I': 9, 'T': 7, 'A': 2, 'O': 3, 'Q': 1, 'N': 9, 'E': 9, 'D': 8, 'R': 6, 'S': 5, 'F': 3, 'H': 5, 'Y': 3, 'L': 4}

>>> sneeuwbal('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
True
>>> sneeuwbal('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
False
>>> sneeuwbal('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
False

>>> pyramide('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
False
>>> pyramide('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
True
>>> pyramide('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
False

>>> pi('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
False
>>> pi('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
False
>>> pi('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
True

Bronnen

Harshbarger E, Keith M (2012). Number Names With A Snowball Letter Distribution, Word Ways 45(4), artikel 10.

Submit solution!

Added by:	Peter Dawyndt
Date:	2015-11-30
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC