| Submit | All submissions | Best solutions | Back to list |
PROG0584 - Drunken ant |
Ants mainly communicate with each other using odorants called pheromones. Like other insects, ants perceive smells with their long, thin, and mobile antennae. The paired antennae provide information about the direction and intensity of scents. Since most ants live on the ground, they use the soil surface to leave pheromone trails that may be followed by other ants. A forager that finds food, marks a trail on the way back to the colony. If this trail is followed by other ants, these ants then reinforce the trail when they head back with food to the colony. When the food source is exhausted, no new trails are marked by returning ants and the scent slowly dissipates.
Foraging ants travel distances of up to 200 meters from their nest and scent trails allow them to find their way back even in the dark. Distances traveled are measured using an internal pedometer that keeps count of the steps taken and also by evaluating the movement of objects in their visual field. Directions are measured using the position of the sun. They integrate this information to find the shortest route back to their nest. Ants that become separated from pheromone trails (for example because they have been moved to another location by a human being) may run around continuously until they die of exhaustion.
Assignment
In this assignment we simulate the behaviour of an ant tracking its way back to the nest by following a disturbed pheromone trail. The environment in which the ant forages is represented by a square $n \times n$ grid having $n$ row and $n$ columns. The ant initially is located in the bottom left corner of the grid and its nest is located in the top right corner of the grid. Each cell in the grid contains a pheromone trail that points up, down, left or right. On each turn in the simulation, the ant moves to the neighbouring cell that is pointed to by the pheromone trail, and then the direction of the trail on the cell that it has left turns 90° clockwise. If the ant is not able to move in the indicated direction because the edge of the grid blocks its path, it remains on its current cell and the direction of the trail on the cell turns 90° clockwise.
The original configuration of a square $n \times n$ grid with pheromone trails is given as a string containg $n^2$ characters, which represent the direction symbols in the grid. The $n \times n$ grid must be filled up from left to right, and from top to bottom, using the sequence of characters in the string. The following four characters are used as direction symbols:
- >: the pheromone trail points to the right
- <: the pheromone trail points to the left
- ^: the pheromone trail points up
- v: the pheromone trail points down
A position in the grid is represented as a tuple whose first element indicates the row index and whose second element indicates the column index. The rows of the grid are index from top to bottom, and the columns from left to right, where indexing starts at zero. Your task:
- Write a function grid that takes an integer $n \in \mathbb{N}_0$ and a string as its arguments. The function must return a list of lists that represents a square $n \times n$ grid with pheromone trails, where the grid must be filled up from left to right, and from top to bottom, using the sequence of characters in the given string. In case the given string does not contain $n^2$ characters, the function must raise an AssertionError with the message invalid arguments.
- Write a function text that takes a square $n \times n$ grid with pheromone trails, represented as a list of lists. The function must return a string containing the representation of the $n \times n$ grid, where all symbols on a given row are separated by spaces, and all rows are on a separate line.
- Write a function step that takes two arguments: i) a square $n \times n$ grid with pheromone trails represented as a list of lists, and ii) a position in the grid. The function must perform a single step of the simulation, with the ant leaving at the given position in the grid. In doing so, the function must modify the pheromone trails at the ant's starting position and return the position of the ant after the simulation step has finished.
- Write a function steps that can be used to perform an entire simulation of the steps taken by the ant from its starting position at the bottom left corner of the grid until it reaches its nest at the top right corner of the grid. The function takes the original configuration of the $n \times n$ grid with pheromone trails, represented as a list of lists. The function must return a list of positions that begins with the original position of the ant at the start of the simulation, followed by the positions of the ant after each step in the simulation. After the function returns, the grid must contain the configuration of pheromone trails at the time the ant has reached its nest.
Example
>>> square = grid(4, '>>>>^<^v^v^^>>v>') >>> square [['>', '>', '>', '>'], ['^', '<', '^', 'v'], ['^', 'v', '^', '^'], ['>', '>', 'v', '>']] >>> print(text(square)) > > > > ^ < ^ v ^ v ^ ^ > > v > >>> step(square, (3, 0)) (3, 1) >>> print(text(square)) > > > > ^ < ^ v ^ v ^ ^ v > v > >>> step(square, (3, 1)) (3, 2) >>> print(text(square)) > > > > ^ < ^ v ^ v ^ ^ v v v > >>> square = grid(4, '>>>>^<^v^v^^>>v>') >>> print(text(square)) > > > > ^ < ^ v ^ v ^ ^ > > v > >>> steps(square) [(3, 0), (3, 1), (3, 2), (3, 2), (3, 1), (3, 1), (3, 0), (3, 0), (3, 0), (2, 0), (1, 0), (0, 0), (0, 1), (0, 2), (0, 3)] >>> print(text(square)) v v v > > < ^ v > v ^ ^ > ^ ^ > >>> grid(4, '>>>>^<^v^v^>>v>') Traceback (most recent call last): AssertionError: invalid arguments
Epilogue
You may have wondered whether it is possible that during a simulation an ant keeps wandering without ever reaching its nest. We can easily prove that an ant will always reach the upper right corner of the grid in a finite number of steps. Suppose by way of contradiction that an ant stays in the grid forever. Because the grid contains a finite number of cells, this means the ant will visit at least one cell an infinite number of times. And because this cell rotates after each visit, it follows that the ant visits each of its adjacent cells an infinite number of times. By extension this means that the ant will visit every cell in the grid an infinite number of times. This includes the cell in the upper right corner. Hence it's not possible for the ant to stay in the grid forever without ever reaching its nest.
Mierencommunicatie verloopt hoofdzakelijk door middel van geurstoffen, die feromonen genoemd worden. Ze worden bijvoorbeeld gebruikt om aan te geven waar er voedsel te vinden is. Zo kan een voedselverzamelaar een spoor op de grond achterlaten om andere voedselverzamelaars te informeren waar er voedsel te vinden is. Mieren die het feromonenspoor volgen, zorgen voor een versterking van het signaal, waardoor nog meer mieren het spoor blijven volgen totdat het voedsel is uitgeput. Het feromonenspoor wordt dan niet langer versterkt en vervaagt langzaam.
Behalve feromonensporen gebruiken mieren verschillende soorten informatie om de weg naar hun nest terug te vinden. Zo tellen ze bijvoorbeeld het aantal stappen dat ze hebben genomen sinds hun vertrek, hebben ze een ingebouwd kompas en slaan ze herkenningspunten op in hun geheugen. Mieren die een feromonenspoor verliezen (bijvoorbeeld omdat ze door een mens op een andere plaats worden neergezet) hebben het vaak moeilijker om hun nest terug te vinden.
Opgave
In deze opgave simuleren we het gedrag van een mier die op basis van een verstoord feromonenspoor de weg naar zijn nest probeert terug te vinden. De omgeving waarin de mier zich beweegt, wordt voorgesteld als een vierkant $n \times n$ rooster met $n$ rijen en $n$ kolommen. De mier bevindt zich initieel in de linkeronderhoek van het rooster en zijn nest bevindt zich in de rechterbovenhoek van het rooster. Elke cel van het rooster bevat een feromonenspoor dat wijst naar boven, onder, links of rechts. Bij elke simulatiestap verplaatst de mier zich naar de naburige cel die wordt aangegeven door het feromonenspoor, waarna de richting van het spoor op de cel die wordt verlaten 90° in wijzerzin gedraaid wordt. Indien de mier niet in de aangegeven richting kan bewegen omdat ze tegen de rand van het rooster aanloopt, blijft ze op haar huidige positie staan, maar wordt de richting van het spoor op de cel wel nog 90° in wijzerzin gedraaid.
De originele configuratie van een vierkant $n \times n$ rooster met feromonensporen wordt gegeven als een string bestaande uit $n^2$ karakters, die de richtingaanwijzers in het rooster voorstellen. De opeenvolgende karakters moeten van links naar rechts en van boven naar onder in het $n \times n$ rooster ingevuld worden. De volgende vier karakters worden gebruikt als richtingaanwijzers:
- >: het feromonenspoor leidt naar rechts
- <: het feromonenspoor leidt naar links
- ^: het feromonenspoor leidt naar boven
- v: het feromonenspoor leidt naar onder
Een positie in het rooster wordt voorgesteld als een tuple waarvan het eerste element de rij-index aangeeft en het tweede element de kolom-index aangeeft. Hierbij worden de rijen van het rooster genummerd van boven naar onder, en de kolommen van links naar rechts, waarbij de nummering telkens start vanaf nul. Gevraagd wordt:
- Schrijf een functie rooster waaraan een natuurlijk getal $n$ en een string moeten doorgegeven worden. De functie moet een lijst van lijsten teruggeven die een $n \times n$ rooster van richtingaanwijzers voorstelt, waarbij de opeenvolgende karakters van de gegeven string van links naar rechts en van boven naar onder in het $n \times n$ rooster moeten ingevuld worden. Indien de gegeven string niet bestaat uit $n^2$ karakters, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige argumenten.
- Schrijf een functie tekst waaraan een $n \times n$ rooster van richtingaanwijzers moet doorgegeven worden, voorgesteld als een lijst van lijsten. De functie moet een string met de voorstelling van het vierkant $n \times n$ rooster teruggeven, waarbij alle symbolen op dezelfde rij van elkaar moeten gescheiden worden door spaties, en alle rijen op afzonderlijke regels moet staan.
- Schrijf een functie stap waaraan twee argumenten moeten doorgegeven worden: i) een $n \times n$ rooster van richtingaanwijzers voorgesteld als een lijst van lijsten, en ii) een positie in het rooster. De functie moet één enkele stap van de simulatie uitvoeren, waarbij de mier vertrekt vanop de aangegeven positie in het rooster. Hierbij moet de functie de richtingaanwijzer op de huidige positie aanpassen, en de nieuwe positie teruggeven waarop de mier zich bevindt na het uitvoeren van de simulatiestap.
- Schrijf een functie stappen waarmee een volledige simulatie wordt uitgevoerd van de bewegingen die de mier maakt vanaf zijn startpositie in de linkeronderhoek van het rooster tot aan zijn nest in de rechterbovenhoek van het rooster. Aan de functie moet de originele configuratie van het $n \times n$ rooster met richtingaanwijzers doorgegeven worden, voorgesteld als een lijst van lijsten. De functie moet een lijst van posities teruggeven die start met de positie in de linkeronderhoek van het rooster, gevolgd door de posities waarop de mier zich bevond na elke stap uit de simulatie. Na het uitvoeren van de functie, moet het rooster de configuratie van de richtingaanwijzers bevatten op het ogenblik dat de mier zijn nest bereikt heeft.
Voorbeeld
>>> vierkant = rooster(4, '>>>>^<^v^v^^>>v>') >>> vierkant [['>', '>', '>', '>'], ['^', '<', '^', 'v'], ['^', 'v', '^', '^'], ['>', '>', 'v', '>']] >>> print(tekst(vierkant)) > > > > ^ < ^ v ^ v ^ ^ > > v > >>> stap(vierkant, (3, 0)) (3, 1) >>> print(tekst(vierkant)) > > > > ^ < ^ v ^ v ^ ^ v > v > >>> stap(vierkant, (3, 1)) (3, 2) >>> print(tekst(vierkant)) > > > > ^ < ^ v ^ v ^ ^ v v v > >>> vierkant = rooster(4, '>>>>^<^v^v^^>>v>') >>> print(tekst(vierkant)) > > > > ^ < ^ v ^ v ^ ^ > > v > >>> stappen(vierkant) [(3, 0), (3, 1), (3, 2), (3, 2), (3, 1), (3, 1), (3, 0), (3, 0), (3, 0), (2, 0), (1, 0), (0, 0), (0, 1), (0, 2), (0, 3)] >>> print(tekst(vierkant)) v v v > > < ^ v > v ^ ^ > ^ ^ > >>> rooster(4, '>>>>^<^v^v^>>v>') Traceback (most recent call last): AssertionError: ongeldige argumenten
Epiloog
Je hebt je misschien wel afgevraagd of het niet mogelijk is dat een mier tijdens de simulatie eeuwig rondjes blijft draaien zonder ooit zijn nest te bereiken. We kunnen echter eenvoudig aantonen dat een mier steeds na een eindig aantal stappen de rechterbovenhoek van het rooster zal bereiken. Veronderstel bij wijze van contradictie dat de mier voor eeuwig en altijd in het rooster blijft rondlopen. Omdat het rooster bestaat uit een eindig aantal cellen, betekent dit dat de mier minstens één cel een oneindig aantal keer bezoekt. Aangezien de richtingaanwijzers bij elke stap draaien, volgt hieruit dat ook elke naburige cel een oneindig aantal keer bezocht wordt. Bij uitbreiding betekent dit ook dat elke cel in het rooster een oneindig aantal keer bezocht wordt, inclusief de cel in de rechterbovenhoek. Bijgevolg is het dus niet mogelijk dat de mier eeuwig in het rooster blijft ronddwalen, zonder de rechterbovenhoek van het rooster te bereiken.
| Added by: | Peter Dawyndt |
| Date: | 2015-10-24 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |


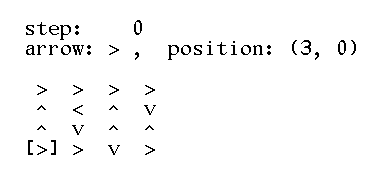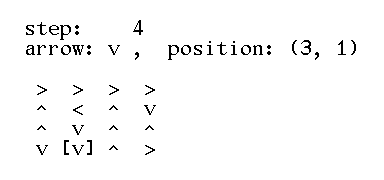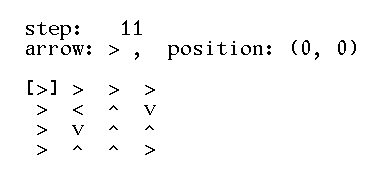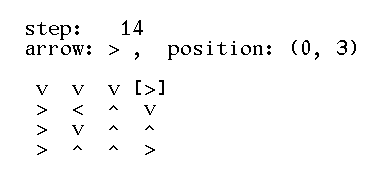
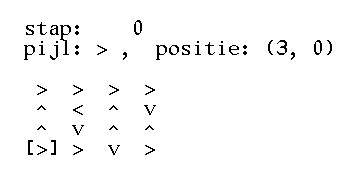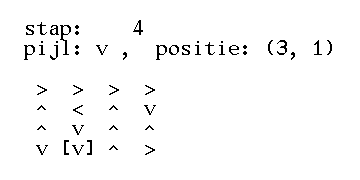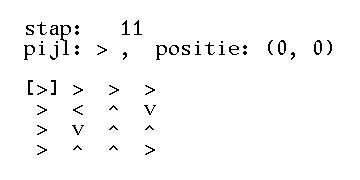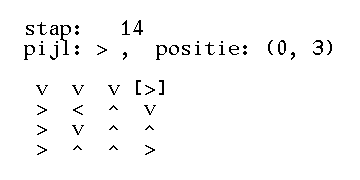
 RSS
RSS