SPOJ.com - Problem PROG0575

PROG0575 - Round numbers

A curiosity attributed to Professor E. Ducci in the 1930s.

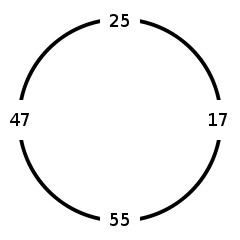
Arrange four non-negative integers in a circle, as above. Now construct another cyclic quadruple of integers by subtracting consecutive pairs, always subtracting the smaller number from the larger number. So the quadruple above would produce a new quadruple 22–8–38–8. If we apply the procedure to this new quadruple, we obtain another quadruple 14–30–30–14, and so on. Ducci found that eventually four equal numbers will occur. A proof appears in Ross Honsberger's Ingenuity in Mathematics (1970).

Input

The input contains four integers, each on a separate line.

Output

The given quadruple of integers is arranged in a circle, with the first integer at the leftmost position and the following integers clockwise around the circle. Then we apply the procedure of Ducci and again arrange the newly obtained quadruple around a circle. The leftmost integer in the new circle indicates the difference between the leftmost and topmost integers in the original circle, the topmost integer in the new circle indicates the difference between the topmost and rightmost integers in the original circle, and so on clockwise around the circle.

The output should contain the sequence of cyclic quadruples obtained when applying the procedure of Ducci to the four given integers. The first circle should represent the cyclic quadruple containing the four given integers, and the last circle should represent the first cyclic quadruple that has four equal integers. For each circle in the sequence, a single line of output must be generated that contains the four integers in the order left-top-right-bottom, separated from each other by dashes (-).

Example

Input:

Output:

47-25-17-55
22-8-38-8
14-30-30-14
16-0-16-0
16-16-16-16

Resources

Gardner M (1987). Riddles of the Sphinx. Mathematical Association of America. ISBN-13: 978-0883856321.
Honsberger R (1970). Ingenuity in Mathematics. Mathematical Association of America. ISBN-13: 978-0883856239.

Een curiositeit uit de jaren '30 die wordt toegeschreven aan professor E. Ducci.

Plaats vier willekeurige gehele getallen in een cirkel, zoals aangegeven in bovenstaand voorbeeld. Bepaal nu een volgend getallenkwartet door het verschil te bepalen van alle opeenvolgende paren getallen, waarbij telkens het kleinste getal wordt afgetrokken van het grootste getal. Het kwartet uit bovenstaand voorbeeld levert op die manier het nieuwe getallenkwartet 22–8–38–8 op. Als we de procedure opnieuw toepassen op dit nieuwe kwartet, dan krijgen we het kwartet 14–30–30–14. Ducci ontdekte dat als we deze procedure blijven herhalen, we uiteindelijk altijd een kwartet van vier gelijke getallen bekomen. Een bewijs hiervan is terug te vinden in een artikel uit Ingenuity in Mathematics van Ross Honsberger (1970).

Invoer

De invoer bestaat uit vier gehele getallen, elk op een afzonderlijke regel.

Uitvoer

We plaatsen de vier gegeven getallen in een cirkel, waarbij we het eerste getal uiterst links plaatsen en de opeenvolgende getallen in wijzerzin rond de cirkel plaatsen. Daarna passen we de procedure van Ducci toe, waarbij we het nieuwe kwartet opnieuw in een cirkel plaatsen. Daarbij is het getal uiterst links van de cirkel het verschil tussen de getallen links en boven in de oorspronkelijke cirkel, het getal bovenaan de nieuwe cirkel is het verschil tussen de getallen boven en rechts in de oorspronkelijke cirkel, en zo lopen we de cirkel verder in wijzerzin af.

Schrijf de opeenvolgende cirkels uit die je bekomt als je achtereenvolgens de procedure van Ducci toepast op de vier gegeven getallen. De eerste cirkel die je moet uitschrijven is de cirkel met de vier gegeven getallen, en de laatste cirkel die je moet uitschrijven is de eerste cirkel waarvoor de vier getallen voor het eerst gelijk zijn. Elke cirkel wordt uitgeschreven op een afzonderlijke regel, waarbij de vier getallen achter elkaar worden uitgeschreven — van elkaar gescheiden door een koppelteken (-) — in de volgorde links–boven–rechts–onder.

Voorbeeld

Invoer:

Uitvoer:

47-25-17-55
22-8-38-8
14-30-30-14
16-0-16-0
16-16-16-16

Bronnen

Gardner M (1987). Riddles of the Sphinx. Mathematical Association of America. ISBN-13: 978-0883856321.
Honsberger R (1970). Ingenuity in Mathematics. Mathematical Association of America. ISBN-13: 978-0883856239.

Submit solution!

Added by:	Peter Dawyndt
Date:	2015-10-13
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC