SPOJ.com - Problem PROG0561

PROG0561 - Busy bees

Drones are male honey bees that are the product of an unfertilized egg. Drones are characterized by eyes that are twice the size of those of worker bees and queens, and a body size greater than that of worker bees, though usually smaller than the queen bee. Their abdomen is stouter than the abdomen of workers or queen. Although heavy bodied, drones must be able to fly fast enough to accompany the queen in flight. Unlike the female worker bee, drones do not have stingers.

Drones do not exhibit typical worker bee behaviours such as nectar and pollen gathering, nursing, or hive construction. Although drones are highly specialized to perform one function — mating and continuing the propagation of the hive — they are not completely without side benefit to the hive. All bees, when they sense the hive's temperature deviating from proper limits, either generate heat by shivering, or exhaust heat by moving air with their wings — behaviours which drones share with worker bees.

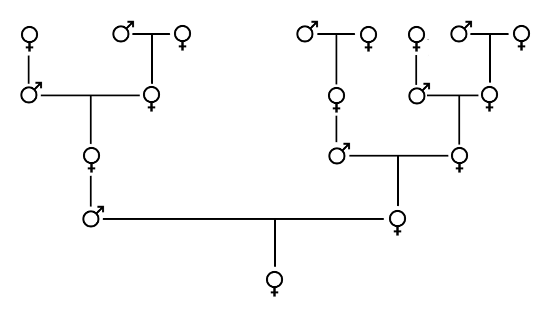
But as stated above, a drone's primary role is to mate with a fertile queen. Just like the eggs from which the workers bees and the next generation of queens are born, the eggs from which the drones are born are laid by the queen itself. As such, drones have mothers but no fathers, but they do have a grandfather. Females come from fertilized eggs, so they have parents of both sexes. This produces an interesting pattern: the number of males in a given generation equals the number of females in the preceding generation, and the number of females in a given generation equals the number of females in the preceding two generations.

generation	0	1	2	3	4	5	6	7
number of female bees	0	1	1	2	3	5	8	13
number of male bees	1	0	1	1	2	3	5	8
total number of bees	1	1	2	3	5	8	13	21

So the total number of bees — male and female — in generation $n$ is the Fibonacci number $F_n$. W. Hope-Jones discovered this relationship in 1921.

Input

The input contains a single integer $n \in \mathbb{N}$ that indicates the index of a generation, where generations are numbered starting from zero. We assume that the first generation (generation 0) exists of a single drone.

Output

Three lines of output need to be generated, which respectively give the number of female bees, the number of male bees, and the total number of bees in generation $n$. Take a look at the example below to see how the output should be formatted.

Example

Input:

Output:

number of female bees: 13
number of male bees: 8
total number of bees: 21

Resource

Hope-Jones W (1921). The Bee and the Regular Pentagon. The Mathematical Gazette X(150), 206.
Koshy T (2001). Fibonacci and Lucas Numbers with Applications. Wiley-Interscience.

Darren zijn mannelijke bijen die geboren worden uit een onbevrucht eitje. Ze zijn een maatje groter dan de werkbijen, maar een maatje kleiner dan de koningin. Hun ogen zijn twee keer zo groot als de ogen van de werkbijen en de koningin, maar in tegenstelling tot de werkbijen kunnen darren niet steken.

Darren halen geen honing, geen stuifmeel, voeren geen larven, bouwen geen raten en laten zich het liefst van al voeren door de werkbijen. Hun bijdrage aan de kolonie is om een klein beetje te helpen bij de temperatuurregeling. Wanneer de temperatuur te laag wordt, gaan de darren en de werkbijen warmte genereren door te trillen en wanneer de temperatuur te hoog wordt, gaan de darren net als alle werkbijen met de vleugels wapperen ter ventilatie.

Daarnaast bestaat de enige andere taak van darren erin om te paren met de koningin. Net zoals de eitjes waaruit werkbijen en volgende generaties koninginnen geboren worden, worden eitjes waaruit de darren geboren worden, gelegd door de koningin zelf. Darren hebben dus een moeder maar geen vader, maar ze hebben wel een grootvader. Vrouwelijke bijen komen uit bevruchte eitjes en hebben dus ouders van beide geslachten. Hierdoor ontstaat een interessant patroon: het aantal darren in een bepaalde generatie is gelijk aan het aantal vrouwelijke bijen in de voorgaande generatie, en het aantal vrouwelijke bijen in een bepaalde generatie is gelijk aan het aantal vrouwelijke bijen in de voorgaande twee generaties.

generatie	0	1	2	3	4	5	6	7
aantal vrouwelijke bijen	0	1	1	2	3	5	8	13
aantal mannelijke bijen	1	0	1	1	2	3	5	8
totaal aantal bijen	1	1	2	3	5	8	13	21

Het totaal aantal bijen — zowel mannelijke als vrouwelijke — in generatie $n$ is hierdoor dus gelijk aan het Fibonaccigetal $F_n$. Dit patroon werd in 1921 ontdekt door W. Hope-Jones.

Invoer

De invoer bestaat uit één getal $n \in \mathbb{N}$ dat het volgnummer van een generatie aangeeft. Generaties worden hierbij genummerd vanaf nul, waarbij we veronderstellen dat de eerste generatie (generatie 0) enkel bestaat uit één mannelijke bij.

Uitvoer

Er moeten drie regels uitvoer gegenereerd worden, die respectievelijk het aantal vrouwelijke bijen, het aantal mannelijke bijen en het totaal aantal bijen in generatie $n$ aangeven. Bekijk onderstaand voorbeeld om te zien hoe de uitvoer precies moet opgemaakt worden.

Voorbeeld

Invoer:

Uitvoer:

aantal vrouwelijke bijen: 13
aantal mannelijke bijen: 8
totaal aantal bijen: 21

Bronnen

Hope-Jones W (1921). The Bee and the Regular Pentagon. The Mathematical Gazette X(150), 206.
Koshy T (2001). Fibonacci and Lucas Numbers with Applications. Wiley-Interscience.

Submit solution!

Added by:	Peter Dawyndt
Date:	2015-09-29
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC