| Submit | All submissions | Best solutions | Back to list |
PROG0556 - Digit work |
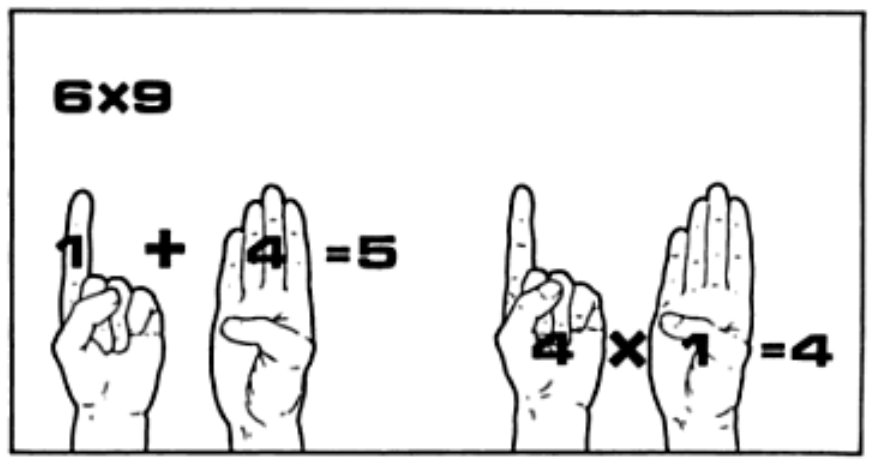
Here's a useful system of finger reckoning from the Middle Ages. To multiply $6 \times 9$, hold up one finger to represent the difference between the five fingers on that hand and the first number to be multiplied. On the other hand hold up four fingers, the difference between five and nine.
Then add the standing fingers and multiply the result by ten to get the tens of the answer ($10 \times (1 + 4) = 50$). In this case there would be five tens, so one would know that the answer would be 50-something. To find the 'something' multiply the closed fingers ($4 \times 1 = 4$), thus reaching the answer of 54. In this way one can multiply numbers between 6 and 9 while only knowing the multiplication table up to $5 \times 5$ and knowing how to multiply by 10.
A similar system could be used to multiply numbers between 10 and 15. To multiply $14 \times 12$ put up four fingers on one hand and two on the other. Add them to get six. Then add 10 times that sum to 100, which would give you 160. Finally add the product of the fingers $(4 \times 2)$ to reach the answer: 168. Again, this only requires to know the multiplication table up to $5 \times 5$ and to know how to multiply by 10.
Both finger reckoning techniques are a direct reflection of the fact that the following general algebraic equation holds for the multiplication of two integers $x$ and $y$ $$xy = 100 + 10 [(x - 10) + (y - 10)] + (x - 10)(y - 10)$$
Input
The input contains two integers $x, y \in \mathbb{N}$ ($0 \leq x, y \leq 20$), each on a separate line.
Output
A single line of output needs to be generated. This line shows how the two given integers can be multiplied using the methods explained above. In order to do so, a distinction must be made between the following cases:
- if both numbers are smaller than or equal to 5, or if at least one of the numbers is equal to 10, the product must be computed directly (see first example)
- if both numbers are between 6 and 9 (including boundaries), the product must be computed using the first method explained above (see second example)
- if both numbers are between 11 and 15 (including boundaries), the product must be computed using the second method explained above (see second example)
- in all other cases the general algebraic equation to compute the product of two given integers must be used (see forth example)
Inspect the examples below to see how the output must be formatted.
Example
case: both numbers are smaller than or equal to 5.
Input:
2 5
Output:
2 x 5 = 10
Example
case: both number are between 6 and 9 (including boundaries).
Input:
6 9
Output:
6 x 9 = 10 x (1 + 4) + (4 x 1) = 54
Example
case: both number are between 11 and 15 (including boundaries).
Input:
14 12
Output:
14 x 12 = 100 + 10 x (4 + 2) + (4 x 2) = 168
Example
case: general algebraic equation to compute the product of two integers.
Input:
4 11
Output:
4 x 11 = 100 + 10 x (-6 + 1) + (-6 x 1) = 44
Resources
In de Middeleeuwen gebruikte men een handige vingertechniek om snel te kunnen vermenigvuldigen. Om bijvoorbeeld de vermenigvuldiging $6 \times 9$ uit te rekenen, steek je één vinger van je linkerhand op om het verschil aan te geven tussen de vijf vingers aan die hand en het eerste getal dat moet vermenigvuldigd worden. Van de rechterhand steek je vier vingers op, namelijk het verschil tussen 9 en 5.
Daarna tel je het aantal opgestoken vingers van beide handen bij elkaar op, en vermenigvuldig je het resultaat met 10 ($10 \times (1 + 4) = 50$). Daarbij tel je het product op van de gesloten vingers van de twee handen ($4 \times 1 = 4$). Dit geeft je het gevraagde resultaat. Deze methode laat toe om het product van twee getallen tussen 6 en 9 berekenen, terwijl je enkel de vermenigvuldigingstabel tot en met $5 \times 5$ moet kennen en ook moet kunnen vermenigvuldigen met 10.
Om twee getallen tussen 10 en 15 met elkaar te vermenigvuldigen kan je een gelijkaardige methode gebruiken. Om bijvoorbeeld de vermenigvuldiging $14 \times 12$ uit te rekenen, steek je vier vingers van de linkerhand op en twee vingers van de rechterhand. Daarna tel je het aantal opgestoken vingers op, vermenigvuldig je het resultaat met 10 en telt er 100 bij op ($100 + 10 \times (4 + 2) = 160$). Daarbij tel je het product op van de opgestoken vingers ($160 + (4 \times 2) = 168$). Ook in dit geval moet je enkel kunnen vermenigvuldigen met tien, en de vermenigvuldigingstabel kennen tot en met $5 \times 5$.
Beide vingertechnieken zijn een direct gevolg van het feit dat voor de vermenigvuldiging van twee natuurlijke getallen $x$ en $y$ de volgende algemene formule geldt $$xy = 100 + 10 [(x - 10) + (y - 10)] + (x - 10)(y - 10)$$
Invoer
De invoer bestaat uit twee getallen $x, y \in \mathbb{N}$ ($0 \leq x, y \leq 20$) die elk op een afzonderlijke regel staan.
Uitvoer
Er moet één regel uitvoer gegenereerd worden, die illustreert hoe de twee getallen met elkaar kunnen vermenigvuldigd worden op basis van de methoden die in de inleiding uitgelegd worden. Hierbij moet onderscheid gemaakt worden tussen de volgende gevallen:
- als beide getallen kleiner of gelijk zijn aan 5 of als minstens één van beide getallen 10 is, dan moet het product rechtstreeks berekend worden (zie eerste voorbeeld)
- als beide getallen tussen 6 en 9 liggen (inclusief grenzen) dan moet het product berekend worden op basis van de eerste methode die beschreven wordt in de inleiding (zie twee voorbeeld)
- als beide getallen tussen 11 en 15 liggen (inclusief grenzen) dan moet het product berekend worden op basis van de tweede methode die beschreven wordt in de inleiding (zie derde voorbeeld)
- voor alle andere gevallen moet de algemene formule gebruikt worden voor de berekening van het product (zie vierde voorbeeld)
Bekijk onderstaande voorbeelden om te achterhalen hoe de uitvoer precies moet opgemaakt worden.
Voorbeeld
geval: beide getallen zijn kleiner of gelijk aan 5.
Invoer:
2 5
Uitvoer:
2 x 5 = 10
Voorbeeld
geval: beide getallen liggen tussen 6 en 9 (grenzen inbegrepen).
Invoer:
6 9
Uitvoer:
6 x 9 = 10 x (1 + 4) + (4 x 1) = 54
Voorbeeld
geval: beide getallen liggen tussen 11 en 15 (grenzen inbegrepen).
Invoer:
14 12
Uitvoer:
14 x 12 = 100 + 10 x (4 + 2) + (4 x 2) = 168
Voorbeeld
geval: algemene formule om het product van twee natuurlijke getallen te berekenen.
Invoer:
4 11
Uitvoer:
4 x 11 = 100 + 10 x (-6 + 1) + (-6 x 1) = 44
Bronnen
| Added by: | Peter Dawyndt |
| Date: | 2015-09-26 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |


 RSS
RSS