| Submit | All submissions | Best solutions | Back to list |
PROG0504 - Reductio ad absurdum |
Forget everything you know about reducing fractions — it turns out you can just cancel common digits of the numerator and denominator:
Not convinced? Then there's nothing wrong with your gut feeling! The above fractions are just a couple of special cases for which the cancelling procedure (which we will refer to as reductio ad absurdum) results in an equivalent fraction. Applied to most other fractions, the procedure results in a different value. Try it out, for example, on the fraction $\frac{12}{13}$.
Assignment
Your task is to check whether it is allowed to apply the reductio ad absurdum technique to a given fraction. To do this, just follow these steps:
- Write a function equivalentFraction that takes four integers $n_1, d_1, n_2, d_2 \in \mathbb{N}_0$. The function must return a boolean value that indicates whether or not the fractions $\frac{n_1}{d_1}$ and $\frac{n_2}{d_2}$ are equivalent. Note that it is better to avoid using floating point division when testing the equivalence, due to possible rounding errors. Instead, it is better to give both fractions a common denominator and then compare their numerators.
- Write a function reduction that takes two integers $n, d \in \mathbb{N}_0$ which respectively represent the numerator and denominator of a fraction. For each common digit of the numerator and denominator, cancel its leftmost occurrence in both the numerator and denominator, until the numerator and denominator have no more digits in common. The function must return two integers that respectively represent the numerator and denominator that result after cancelling the common digits. If all digits of the numerator have been cancelled, the first value returned must be -1. Similar, the second value returned should be -1 if all digits of the denominator have been cancelled.
- Use the functions equivalentFraction and reduction to write a function validReduction that takes two integers $n, d \in \mathbb{N}_0$ which respectively represent the numerator and denominator of a fraction. The function validReduction must return the same value as the function reduction in case the reduced fraction turns out to be valid. The latter is the case if the following conditions are fulfilled:
- both the numerator and denominator contain at least one digit after reduction
- the denominator is different from zero after reduction (division by zero is invalid)
- the reduced fraction is equivalent to the original fraction before reduction (sensu the definition of equivalence as implemented by the function equivalentFraction)
Example
>>> equivalentFraction(19, 95, 1, 5) True >>> equivalentFraction(532, 931, 52, 91) True >>> equivalentFraction(12, 13, 2, 3) False >>> reduction(19, 95) (1, 5) >>> reduction(532, 931) (52, 91) >>> reduction(2349, 9396) (24, 96) >>> reduction(12, 13) (2, 3) >>> reduction(11, 10) (1, 0) >>> reduction(123, 3214) (-1, 4) >>> validReduction(19, 95) (1, 5) >>> validReduction(532, 931) (52, 91) >>> validReduction(2349, 9396) (24, 96) >>> validReduction(12, 13) (12, 13) >>> validReduction(11, 10) (11, 10) >>> validReduction(123, 3214) (123, 3214)
Vergeet alles wat je dacht te weten over het vereenvoudigen van breuken — onderstaande voorbeelden tonen aan dat je breuken simpelweg kunt vereenvoudigen door alle gemeenschappelijk cijfers in de teller en de noemer te schrappen:
Niet overtuigd? Dan heeft je buikgevoel het inderdaad bij het rechte eind! Bovenstaande breuken zijn enkel maar speciale gevallen waarvoor de reductio ad absurdum methode op een geldige manier kan toegepast worden, maar voor de meeste andere breuken levert de methode een verschillend resultaat op. Probeer het bijvoorbeeld maar eens uit op de breuk $\frac{12}{13}$.
Opgave
Voor deze opgave moet moet je nagaan of het toegelaten is om de techniek van reductio ad absurdum toe te passen op een gegeven breuk. Hiervoor ga je als volgt te werk:
- Schrijf een functie gelijkeBreuk waaraan vier getallen $t_1, n_1, t_2, n_2 \in \mathbb{N}_0$ moeten doorgegeven worden. De functie moet een Booleaanse waarde teruggeven die aangeeft of de breuken $\frac{t_1}{n_1}$ en $\frac{t_2}{n_2}$ al dan niet gelijk zijn. Merk op dat het omwille van afrondingsfouten onveilig is om de gelijkheid te testen door reële delingen uit te voeren. In plaats daarvan kan je best eerst de breuken op gelijke noemer plaatsen alvorens ze met elkaar te vergelijken.
- Schrijf een functie reductie waaraan twee getallen $t, n \in \mathbb{N}_0$ moeten doorgegeven worden die respectievelijk de teller en de noemer van een breuk voorstellen. Voor elk cijfer uit de teller dat ook in de noemer voorkomt, moet de functie het meest links voorkomen van dat cijfer schrappen uit zowel de teller als de noemer, en dit totdat de teller en de noemer geen gemeenschappelijke cijfers meer hebben. De functie moeten als resultaat twee integers teruggeven die respectievelijk de teller en de noemer voorstellen na het schrappen van de gemeenschappelijke cijfers. Indien alle cijfers uit de teller geschrapt werden, dan moet de eerste waarde die teruggegeven wordt -1 zijn. Hetzelfde geldt voor de tweede waarde die wordt teruggegeven indien alle cijfers uit de noemer geschrapt werden.
- Gebruik de functies gelijkeBreuk en reductie om een functie geldigeReductie te schrijven. Aan deze functie moeten twee getallen $t, n \in \mathbb{N}_0$ doorgegeven worden die respectievelijk de teller en de noemer van een breuk voorstellen. De functie geldigeReductie moet hetzelfde resultaat teruggeven als de functie reductie indien de gereduceerde breuk geldig blijkt te zijn. Dit laatste is het geval als de volgende voorwaarden voldaan zijn:
- na reductie blijven er nog cijfers over in de teller en de noemer
- na reductie mag de noemer niet nul zijn (de noemer van een breuk mag niet nul zijn)
- de waarde van de breuk na reductie is dezelfde als de waarde van de breuk voor reductie (conform de definitie van gelijkheid zoals geïmplementeerd door de functie gelijkeBreuk)
Voorbeeld
>>> gelijkeBreuk(19, 95, 1, 5) True >>> gelijkeBreuk(532, 931, 52, 91) True >>> gelijkeBreuk(12, 13, 2, 3) False >>> reductie(19, 95) (1, 5) >>> reductie(532, 931) (52, 91) >>> reductie(2349, 9396) (24, 96) >>> reductie(12, 13) (2, 3) >>> reductie(11, 10) (1, 0) >>> reductie(123, 3214) (-1, 4) >>> geldigeReductie(19, 95) (1, 5) >>> geldigeReductie(532, 931) (52, 91) >>> geldigeReductie(2349, 9396) (24, 96) >>> geldigeReductie(12, 13) (12, 13) >>> geldigeReductie(11, 10) (11, 10) >>> geldigeReductie(123, 3214) (123, 3214)
| Added by: | Peter Dawyndt |
| Date: | 2014-08-29 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


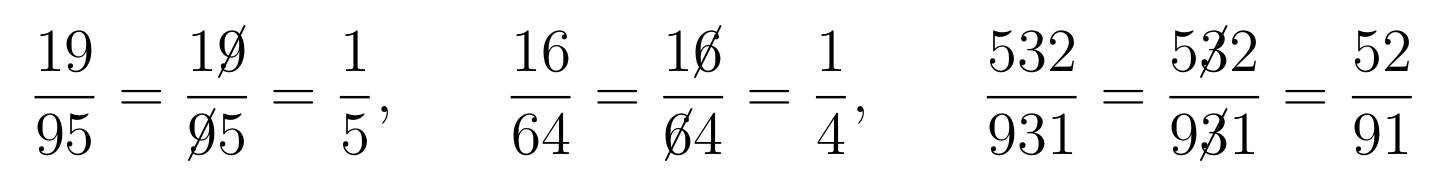
 RSS
RSS