| Submit | All submissions | Best solutions | Back to list |
PROG0492 - Elevator paradox |
The elevator paradox is a paradox first noted in the 1950s by Moritz Stern and George Gamow. Both physicists had offices on different floors of a multi-story building. Gamow, who had an office on the second floor of the building, noticed that the first elevator to stop at his floor was most often going down. Stern, who had an office near the top, noticed that the first elevator to stop at his floor was most often going up.
At first sight, it was as if elves were manufacturing elevator cars in the middle of the building and sent them upwards to the roof or downwards to the basement to be dismantled. You can observe the same phenomenon in most tall buildings, and there are no elves involved. Do you see why it occurs?
Suppose you are at one of the bottom floors of a building. In this case, a single elevator spends most of its time in the top section of the building. If we start waiting for an elevator at a random point in time, it will thus be more likely that the first elevator approaches from the top direction and continues downwards. The opposite is true if we are at one of the top floors of te building.
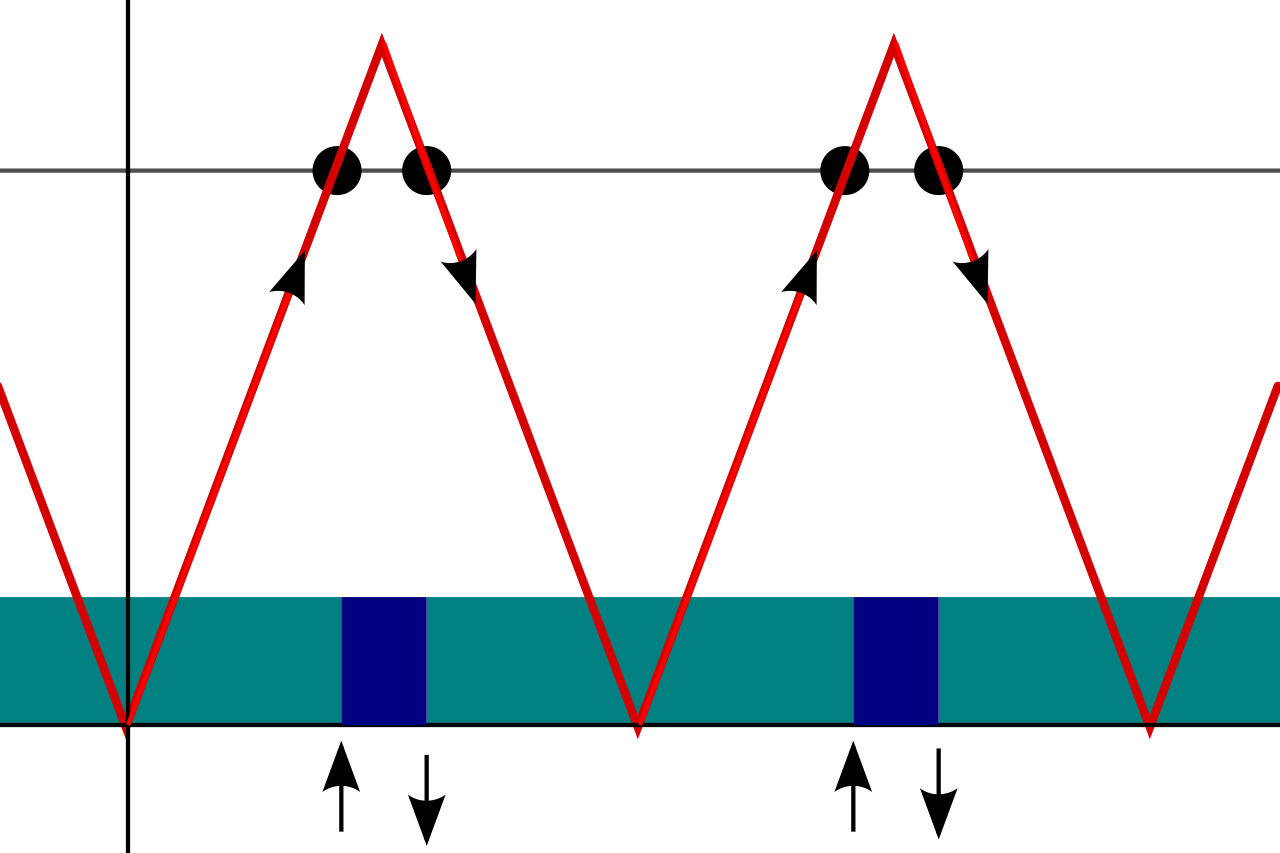
To help visualize this, consider a thirty-story building — plus lobby — with only one slow elevator. The elevator is so slow because it stops at every floor on the way up, and then on every floor on the way down. It takes a minute to travel between floors and wait for passengers. Here is the arrival schedule for people unlucky enough to work in this building. As depicted in the above figure, it forms a triangle wave.
| floor | time on way up | time on way down |
|---|---|---|
| lobby | 8:00, 9:00, … | n/a |
| 1st floor | 8:01, 9:01, … | 8:59, 9:59, … |
| 2nd floor | 8:02, 9:02, … | 8:58, 9:58, … |
| … | … | … |
| 29th floor | 8:29, 9:29, … | 8:31, 9:31, … |
| 30th floor | n/a | 8:30, 9:30, … |
If you were on the first floor and walked up randomly to the elevator, chances are the next elevator would be heading down. The next elevator would be heading up only during the first two minutes at each hour, e.g. at 9:00 and 9:01. The number of elevator stops going upwards and downwards are the same, but the odds that the next elevator is going up is only 2 in 60.
Input
Your task is to generate the arrival schedule for a slow elevator that stops at every floor and takes a minute to travel between floors and wait for the passengers. At the start of the simulation, the elevator is at a given floor and moves in a given direction. If the elevator reaches the lobby, it continues going up. If the elevator reaches the top floor, in continues going down.
There are seven lines of input, containing the following information that must be used to simulate the trajectory of the elevator:
- number of simulated steps ($\in \mathbb{N}$); each floor visited by the elevator — including the floor at the start of the simulation — forms a single step in the simulation
- number $i \in \mathbb{N}$ ($0 \le i \le k$) of the floor where the simulation starts; lobby is assigned number 0
- number $k \in \mathbb{N}_0$ assigned to the top floor
- character that indicates whether the elevator initially goes up or down at the start of the simulation; a caret (circumflex accent; ^) indicates that the elevator initially goes up; a letter v indicates that the elevator initially goes down
- number of hours on a 24-hour clock at the start of the simulation; for example, 23 if simulation starts at 23:14
- number of minutes on a 24-hour clock at the start of the simulation; for example, 14 if simulation starts at 23:14
- text that indicates the amount of detail for the output of the simulation; the text verbose indicates that output needs to be generated during each step of the simulation; the text quiet indicates that output only needs to be generated if the elevator visits floor $i$
Output
The elevator starts at floor $i$ and starts moving in the given direction. For each floor that needs to be included in the arrival schedule, a line must be written to output that contains the current time, the number of the floor that is visited by the elevator, and the direction into which the elevator leaves the current floor (^ if the elevator continues going up, and v is the elevator continues going down). Derive the format of the output from the examples given below. If the last line of the input contains the text verbose, all floors visited by the elevator during the simulated must be included in the arrival schedule. If the last line of the input contains the text quiet, only floor $i$ at which simulation starts must be included in the arrival schedule.
Example
Input:
30 6 8 ^ 23 50 verbose
Output:
23:50 6 [^] 23:51 7 [^] 23:52 8 [v] 23:53 7 [v] 23:54 6 [v] 23:55 5 [v] 23:56 4 [v] 23:57 3 [v] 23:58 2 [v] 23:59 1 [v] 00:00 0 [^] 00:01 1 [^] 00:02 2 [^] 00:03 3 [^] 00:04 4 [^] 00:05 5 [^] 00:06 6 [^] 00:07 7 [^] 00:08 8 [v] 00:09 7 [v] 00:10 6 [v] 00:11 5 [v] 00:12 4 [v] 00:13 3 [v] 00:14 2 [v] 00:15 1 [v] 00:16 0 [^] 00:17 1 [^] 00:18 2 [^] 00:19 3 [^]
Example
Input:
30 6 8 v 9 30 quiet
Output:
09:30 6 [v] 09:42 6 [^] 09:46 6 [v] 09:58 6 [^]
De liftparadox is een paradox die rond 1950 voor het eerst werd opgemerkt door Moritz Stern en George Gamow. Beide fysici hadden hun kantoor op verschillende verdiepingen van hetzelfde gebouw. Gamow had een kantoor op de tweede verdieping en merkte op dat de eerste lift die stopte op zijn verdieping doorgaans op weg was naar beneden. Stern had een kantoor op één van de hoogste verdiepingen en merkte op dat de eerste lift die stopte op zijn verdieping doorgaans naar boven ging.
Op het eerste gezicht leek dit de indruk te wekken dat er ergens in het midden van het gebouw liften gefabriceerd werden die ofwel naar boven of naar beneden gestuurd werden om terug afgebroken te worden op het dak of in de kelder. Dat was natuurlijk niet het geval, en dus moest er wel een logische verklaring zijn voor dit fenomeen.
Stel dat we ons bijvoorbeeld op één van de onderste verdiepingen bevinden. In dat geval zal de lift het grootste deel van zijn tijd doorbrengen op de verdiepingen boven ons. Als we op een willekeurig tijdstip op de lift gaan wachten, dan is het dus meest waarschijnlijk dat de eerstvolgende lift die op onze verdieping passeert van boven toekomt en naar beneden zal gaan. Het omgekeerde is het geval als we ons op één van de bovenste verdiepingen bevinden.
Om het wat concreter te maken, beschouwen we een gebouw met dertig verdiepingen — plus het gelijkvloers — waarin slechts één trage lift beschikbaar is. De lift is zo traag omdat ze op elke verdieping stopt op weg naar boven, en daarna terug op elke verdieping stopt op weg naar beneden. In totaal duurt het één minuut om van een verdieping naar de volgende verdieping te gaan en te wachten tot alle passagiers zijn in- of uitgestapt. Hieronder staat het tijdsschema voor de personen die het ongeluk hebben om in dit gebouw te werken. Zoals ook al bleek uit bovenstaande figuur vormt het traject van de lift een driehoeksgolf.
| verdieping | lift naar boven | lift naar beneden |
|---|---|---|
| gelijkvloers | 8:00, 9:00, … | nvt |
| 1e verdieping | 8:01, 9:01, … | 8:59, 9:59, … |
| 2e verdieping | 8:02, 9:02, … | 8:58, 9:58, … |
| … | … | … |
| 29e verdieping | 8:29, 9:29, … | 8:31, 9:31, … |
| 30e verdieping | nvt | 8:30, 9:30, … |
Als je je bijvoorbeeld op de eerste verdieping van dit gebouw bevindt en op een willekeurig tijdstip naar de lift zou stappen, dan is de kans groot dat de eerstvolgende lift die toekomt op weg is naar beneden. De eerstvolgende lift gaat enkel naar boven tijdens de eerste twee minuten na het uur, bijvoorbeeld om 9:00 en 9:01. Het aantal plaatsen waar de lift stop op weg naar boven en op weg naar beneden mag dan wel hetzelfde zijn, de kans dat de volgende lift naar boven gaat is slechts 2 op 60.
Invoer
Je opdracht bestaat erin een tijdsschema op te stellen van een trage lift die elke verdieping aandoet en er telkens één minuut over doet om naar de volgende verdieping te gaan. Bij aanvang van de simulatie bevindt de lift zich op een bepaalde verdieping en beweegt in een bepaalde richting. Nadat de lift het gelijksvloer bereikt heeft, gaat ze terug naar boven. Nadat de lift de hoogste verdieping bereikt heeft, zal ze terug naar beneden gaan.
De invoer bestaat uit zeven regels, die achtereenvolgens de volgende informatie bevatten die je moet gebruiken om het traject van de lift te simuleren:
- aantal stappen in de simulatie ($\in \mathbb{N}$); elke verdieping die door de lift bezocht wordt — inclusief de startverdieping — vormt één enkele stap in de simulatie
- nummer $i \in \mathbb{N}$ ($0 \le i \le k$) van de verdieping waarop we simulatie start; gelijkvloers krijgt nummer 0
- nummer $k \in \mathbb{N}_0$ van de hoogste verdieping
- karakter dat aangeeft of de lift naar boven of naar beneden gaat bij aanvang van de simulatie; een hoedje (accent circonflexe; ^) geeft aan dat de lift initieel naar boven gaat; de letter v geeft aan dat de lift initieel naar beneden gaat
- aantal uren op een 24-uursklok van het tijdstip bij start van de simulatie; bijvoorbeeld 23 wanneer de simulatie start om 23:14
- aantal minuten op een 24-uursklok van het tijdstip bij start van de simulatie; bijvoorbeeld 14 wanneer de simulatie start om 23:14
- tekst die aangeeft hoe gedetailleerd de informatie over de simulatie moet uitgeschreven worden; de tekst alles geeft aan dat er voor elke stap informatie moet uitgeschreven worden; de tekst stil geeft aan dat er enkel informatie moet uitgeschreven worden als de lift zich op verdieping $i$ bevindt
Uitvoer
De lift start op de aangegeven verdieping met nummer $i$ en beweegt in de opgegeven richting. Voor elke verdieping die in het tijdschema moet opgenomen worden, wordt er een regel uitgeschreven met het tijdstip, het nummer van de verdieping en de beweginsrichting (^ als de lift vanaf deze verdieping naar boven gaat en v als de lift vanaf deze verdieping naar beneden gaat). Leid het formaat van de uitvoer af uit onderstaande voorbeelden. Als de laatste regel van de invoer de tekst alles bevat, dan moeten alle verdiepingen die de lift tijdens de simulatie aandoet in het tijdsschema opgenomen worden. Als de laatste regel van de invoer de tekst stil bevat, dan moet enkel de startverdieping $i$ in het tijdsschema opgenomen worden.
Voorbeeld
Invoer:
30 6 8 ^ 23 50 alles
Uitvoer:
23:50 6 [^] 23:51 7 [^] 23:52 8 [v] 23:53 7 [v] 23:54 6 [v] 23:55 5 [v] 23:56 4 [v] 23:57 3 [v] 23:58 2 [v] 23:59 1 [v] 00:00 0 [^] 00:01 1 [^] 00:02 2 [^] 00:03 3 [^] 00:04 4 [^] 00:05 5 [^] 00:06 6 [^] 00:07 7 [^] 00:08 8 [v] 00:09 7 [v] 00:10 6 [v] 00:11 5 [v] 00:12 4 [v] 00:13 3 [v] 00:14 2 [v] 00:15 1 [v] 00:16 0 [^] 00:17 1 [^] 00:18 2 [^] 00:19 3 [^]
Voorbeeld
Invoer:
30 6 8 v 9 30 stil
Uitvoer:
09:30 6 [v] 09:42 6 [^] 09:46 6 [v] 09:58 6 [^]
| Added by: | Peter Dawyndt |
| Date: | 2014-08-29 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS