| Submit | All submissions | Best solutions | Back to list |
PROG0486 - Monsters and hats |
Two people
find themselves stuck on a remote island. One day, a terrible monster
appears. The monster says that he intends to eat the pair, but will give
them the following chance to survive: later that day, the monster will
line them up face-to-face. The monster will then place either a black or
white hat on each person's head. Each person can see the hat on his or
her counterpart, but cannot see his or her own hat.
The monster will then ask both people at once to simultaneously guess
the color of his or her own hat. The person can say only one word
— either white or black. If both people are
wrong, the monster will devour them on the spot. Otherwise they can go
free. The two people have all afternoon to plan their strategy. The
question is — what should they do?
There exists a rock-solid strategy that will lead to exactly one person guessing correctly. It's easiest to explain this strategy by observing that either the hats have the same or a different color. That is the paradigm shift you have to make to understand that the strategy simply is to decide which of the two players will guess same and which will guess different, based on what they see. In other words, the persons have to agree who will always call out whatever color hat he or she sees on the other person's head, and who will call out the opposite color of what he or she sees. This will, incredibly, always allow one person to guess his or her own hat color correctly, and thereby saving both from being devoured by the terrible monster.
Input
The first two lines each contain the color of the hat that is on the head of the first, respectively the second person: black or white. The third line of input contains an integer (1 of 2) that indicates which of the two persons will say the opposite color he or she sees on the head of the counterpart. The other person will say the same color.
Output
Write two lines of output that contain the color (black or white) that is given as the answer by the first, respectively the second person, based on the strategy as explained above.
Example
Input:
white black 2
Output:
black
black
Op een afgelegen eiland wonen slechts twee personen. Op een dag verschijnt er een verschrikkelijk monster op het eiland. Het monster zegt dat het van plan is om de twee personen op te eten, maar dat ze nog de volgende kans krijgen om te overleven: later die dag zal het monster de twee personen tegenover elkaar opstellen met het gezicht naar elkaar. Het monster zal dan op het hoofd van elke persoon een zwarte of een witte hoed zetten. Elke persoon kan de hoed zien op het hoofd van de andere persoon, maar kan zijn of haar eigen hoed niet zien.
Het monster zal dan aan beide personen vragen om onmiddellijk en tegelijkertijd te raden welke kleur de hoed heeft die op zijn of haar hoofd staat. De persoon mag slechts één enkel woord zeggen — ofwel wit of zwart. Als beide personen het verkeerde antwoord geven, dan zal het monster ze ter plekke verslinden. Anders worden ze vrijgelaten. De twee personen krijgen een namiddag de tijd om hun strategie te plannen. De vraag is — hoe moeten ze het aanpakken?
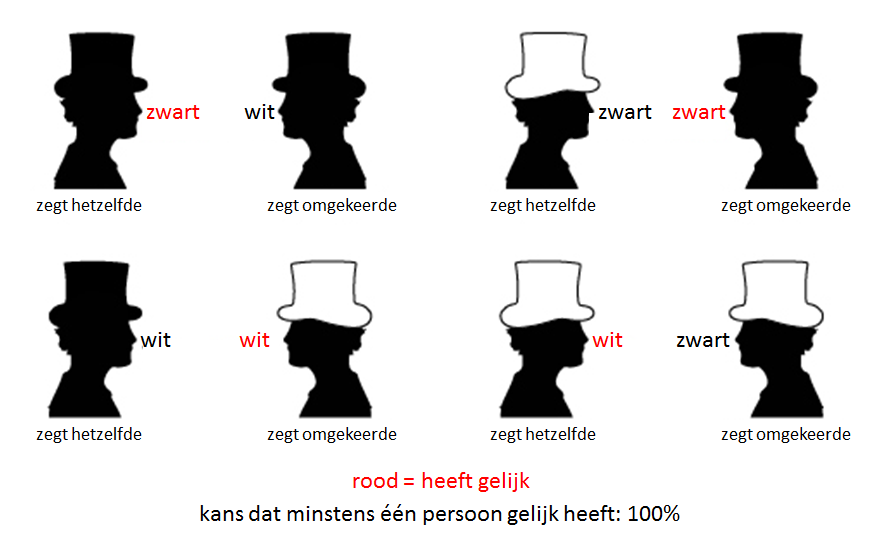
Er bestaat een onfeilbare strategie die garandeert dat er altijd juist één persoon de juiste kleur als antwoord geeft. De makkelijkste manier om deze strategie uit te leggen is door vast te stellen dat de twee hoeden ofwel dezelfde kleur of een verschillende kleur hebben. Als je dat eenmaal doorhebt, dan bestaat de strategie erin te beslissen wie van beide personen hetzelfde zal zeggen en wie verschillend zal zeggen op basis van de kleur van de hoed die ze te zien krijgen. Met andere woorden, de personen moeten afspreken dat één persoon altijd de kleur van de hoed zal zeggen die hij of zij ziet, en dat de andere persoon altijd de omgekeerde kleur zal zeggen die hij of zij ziet. Het lijkt misschien onwaarschijnlijk, maar uit onderstaande afbeelding blijkt dat deze strategie er altijd toe zal leiden dat juist één van de twee personen het juiste antwoord zal geven, en hen daardoor redt om door het monster verslonden te worden.
Invoer
De eerste twee regels bevatten telkens de kleur van de hoed die op het hoofd staat van respectievelijk de eerste en de tweede persoon: zwart of wit. De derde regel bevat een getal (1 of 2) dat aangeeft wie van de twee personen de omgekeerde kleur zal zeggen. De andere persoon zegt dan dezelfde kleur.
Uitvoer
De uitvoer bestaat uit twee regels, die de kleur bevatten (zwart of wit) die als antwoord gegeven wordt door respectievelijk de eerste en de tweede persoon, op basis van de strategie zoals hierboven uitgelegd.
Voorbeeld
Invoer:
wit zwart 2
Uitvoer:
zwart
zwart
| Added by: | Peter Dawyndt |
| Date: | 2014-08-18 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |



 RSS
RSS