SPOJ.com - Problem PROG0309

PROG0309 - Roadmap

The square cells of a rectangular grid are filled with one of the building blocks below, forming a roadmap. The possible building blocks are (from left to right) i) empty cells, ii) cells with one junction (end points), iii) cells with two opposite junctions (straight lanes), iv) cells with two adjacent junctions (curves) and v) cells with four junctions (crossroads). Each of these building blocks can be rotated over an angle of 90°. This gives four possible end points, two possible straight lanes (horizontal and vertical) and four possible curves.

Building blocks for building a street map: i) empty cell, ii) cell with one junction (an end point), iii) cell with two opposite junctions, iv) cell with two adjacent junctions (a curve) and v) cell with four junctions (crossroads).

The roadmap is built in such a way that neighbouring cells always have adjacent junctions. Moreover, the roadmap map always links two ending points, if we always continue straight ahead at every crossroads. All ending points are indicated with a unique uppercase letter.

Example of a roadmap that links the following ending points: A-B, C-D, E-F en G-H.

A roadmap with $m$ rows and $n$ columns can be saved in a text file of $n$ lines, that each consist of $m$ characters, as follows:

empty cells are represented by a space
ending points are represented by the uppercase letter that is used to indicate them
horizontal lanes are represented by a hyphen (-)
vertical lanes are represented by a vertical line (|)
both curves and crossroads are represented by a plus sign (+)

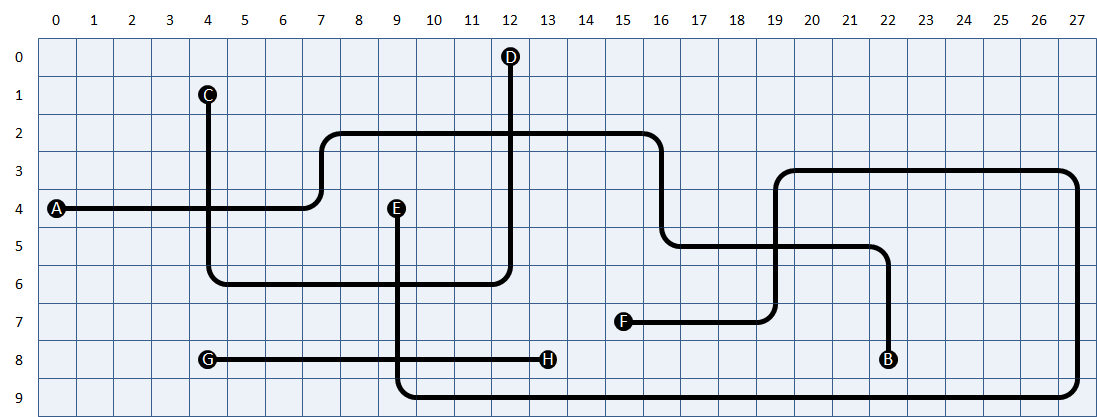
To determine whether a plus sign indicates a bow or a crossroads, you must verify the number of junctions a cell has with its neighbouring cells above, underneath, left and right. The file streetmap1.txt, for example, contains the street map that was given as an example above.

Assignment

Define a class Streetmap that can be used to determine the positions of the ending points for a given street map that was saved in a text file, and which ending points are linked. The objects of the class must contain at least the following methods:

An initializing method to which the location of a text file can be passed. This text file must contain the representation of a street map.
A method rows (without arguments) that prints the number of rows from the street map.
A method columns (without arguments) that prints the number of columns from the street map.
A method location to which the uppercase letter from an ending point must be passed. The method must print a tuple that contains the row and column number of the cell in the grid on which the ending point is situated. Row and columns are numbered from zero, as indicated in the above example. If no ending point is situated in the street map that is indicated with the given uppercase letter, the method must raise an AssertionError with the message unknown end point.
A method connection to which the uppercase letter from an ending point must be given. The method must print the uppercase letter from the ending point with which the given ending point is linked by the street map. If no ending point can be found with the given uppercase letter in the street map, the method must raise an AssertionError with the message unknown end point.

Example

For the below example session, we assume that the files streetmap1.txt and streetmap2.txt are in the current directory.

>>> map = RoadMap('roadmap1.txt')
>>> map.rows()
10
>>> map.columns()
28

>>> map.location('A')
(4, 0)
>>> map.location('F')
(7, 15)

>>> map.connection('A')
'B'
>>> map.connection('B')
'A'
>>> map.connection('C')
'D'
>>> map.connection('D')
'C'
>>> map.connection('E')
'F'
>>> map.connection('F')
'E'
>>> map.connection('G')
'H'
>>> map.connection('H')
'G'
>>> map.connection('X')
Traceback (most recent call last):
AssertionError: unknown end point

>>> map = RoadMap('roadmap2.txt')
>>> map.connection('A')
'B'
>>> map.connection('B')
'A'
>>> map.connection('C')
'D'
>>> map.connection('D')
'C'
>>> map.connection('E')
'F'
>>> map.connection('F')
'E'
>>> map.connection('G')
'H'
>>> map.connection('H')
'G'
>>> map.connection('X')
Traceback (most recent call last):
AssertionError: unknown end point

De vierkante cellen van een rechthoekig rooster worden ingevuld worden met één van de onderstaande bouwstenen, waardoor een stratenplan gevormd wordt. De mogelijke bouwstenen zijn (van links naar rechts) i) lege cellen, ii) cellen met één verbindingspunt (eindpunten), iii) cellen met twee overstaande verbindingspunten (rechte wegen), iv) cellen met twee aanliggende verbindingspunten (bochten) en v) cellen met vier verbindingspunten (kruispunten). Elk van deze bouwstenen kan telkens over een hoek van 90° gedraaid worden. Dit geeft vier mogelijke eindpunten, twee mogelijke rechte wegen (horizontaal en verticaal) en vier mogelijke bochten.

Bouwstenen voor het opbouwen van een stratenplan: i) lege cel, ii) cel met één verbindingspunt (een eindpunt), iii) cel met twee overstaande verbindingspunten, iv) cel met twee aanliggende verbindingspunten (een bocht) en v) cel met vier verbindingspunten (een kruispunt).

Het stratenplan wordt zo opgebouwd dat naburige cellen telkens aaneengesloten verbindingspunten hebben. Bovendien worden door het stratenplan telkens twee eindpunten met elkaar verbonden, als er bij een kruispunt telkens rechtdoor gegaan wordt. Alle eindpunten worden aangeduid met een unieke hoofdletter.

Voorbeeld van een stratenplan dat de volgende eindpunten met elkaar verbindt: A-B, C-D, E-F en G-H.

Een stratenplan met $m$ rijen en $n$ kolommen kan op de volgende manier opgeslaan worden in een tekstbestand dat $n$ regels bevat, die elk bestaan uit $m$ karakters:

lege cellen worden voorgesteld door een spatie
eindpunten worden voorgesteld door de hoofdletter waarmee ze aangeduid worden
horizontale wegen worden worden voorgesteld door een koppelteken (-)
verticale wegen worden voorgesteld door een verticale streep (|)
zowel bochten als kruispunten worden voorgesteld door een plusteken (+)

Om uit te maken of een plusteken een bocht, dan wel een kruispunt voorstelt, moet dus nagegaan worden hoeveel verbindingspunten de cel heeft met zijn naburige cellen boven, onder, links en rechts. Het bestand stratenplan1.txt bevat bijvoorbeeld het stratenplan dat hierboven als voorbeeld gegeven werd.

Opgave

Definieer een klasse Stratenplan die kan gebruikt worden om voor een gegeven stratenplan dat in een tekstbestand is opgeslaan te bepalen waar de eindpunten gepositioneerd zijn, en welke eindpunten met elkaar verbonden zijn. De objecten van deze klasse moeten minstens over de volgende methoden beschikken:

Een initialisatiemethode waaraan de locatie van een tekstbestand kan doorgegeven worden. Dit tekstbestand moet de voorstelling van een stratenplan bevatten.
Een methode rijen (zonder argumenten) die het aantal rijen van het stratenplan teruggeeft.
Een methode kolommen (zonder argumenten) die het aantal kolommen van het stratenplan teruggeeft.
Een methode locatie waaraan de hoofdletter van een eindpunt moet doorgegeven worden. De methode moet een tuple teruggeven dat het rij- en kolomnummer bevat van de cel in het rooster waarop het eindpunt zich bevindt. Rij- en kolomnummers worden genummerd vanaf nul, zoals aangegeven in bovenstaand voorbeeld. Indien er zich in het stratenplan geen eindpunt bevindt dat wordt aangeduid met de opgegeven hoofdletter, dan moet de methode een AssertionError opwerpen met de boodschap onbekend eindpunt.
Een methode verbinding waaraan de hoofdletter van een eindpunt moet doorgegeven worden. De methode moet de hoofdletter teruggeven van het eindpunt waarmee het opgegeven eindpunt verbonden is door het stratenplan. Indien er zich in het stratenplan geen eindpunt bevindt dat wordt aangeduid met de opgegeven hoofdletter, dan moet de methode een AssertionError opwerpen met de boodschap onbekend eindpunt.

Voorbeeld

Bij onderstaande voorbeeldsessie gaan we ervan uit dat de bestanden stratenplan1.txt en stratenplan2.txt zich in de huidige directory bevinden.

>>> plan = Stratenplan('stratenplan1.txt')
>>> plan.rijen()
10
>>> plan.kolommen()
28

>>> plan.locatie('A')
(4, 0)
>>> plan.locatie('F')
(7, 15)

>>> plan.verbinding('A')
'B'
>>> plan.verbinding('B')
'A'
>>> plan.verbinding('C')
'D'
>>> plan.verbinding('D')
'C'
>>> plan.verbinding('E')
'F'
>>> plan.verbinding('F')
'E'
>>> plan.verbinding('G')
'H'
>>> plan.verbinding('H')
'G'
>>> plan.verbinding('X')
Traceback (most recent call last):
AssertionError: onbekend eindpunt

>>> plan = Stratenplan('stratenplan2.txt')
>>> plan.verbinding('A')
'B'
>>> plan.verbinding('B')
'A'
>>> plan.verbinding('C')
'D'
>>> plan.verbinding('D')
'C'
>>> plan.verbinding('E')
'F'
>>> plan.verbinding('F')
'E'
>>> plan.verbinding('G')
'H'
>>> plan.verbinding('H')
'G'
>>> plan.verbinding('X')
Traceback (most recent call last):
AssertionError: onbekend eindpunt

Submit solution!

Added by:	Peter Dawyndt
Date:	2013-01-19
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None