| Submit | All submissions | Best solutions | Back to list |
PROG0121 - Powerful numbers |
Powerful numbers are positive integers that equal the sum of the $n$-th powers of their digits for some $n \in \mathbb{N}$. The smallest $n$ for which this property holds is called the order of the powerful number.
Consider, for example, the number 912985153. This is a powerful number of order 9 because $$9^9 + 1^9 + 2^9 + 9^9 + 8^9 + 5^9 + 1^9 + 5^9 + 3^9 = 912985153$$
Input
A positive integer.
Output
A line that indicates whether or not the given integer is a powerful number. In case the given number is a powerful number, the output must also indicate the order of the powerful number. The format of the output can be derived from the examples below.
Example
Input:
912985153
Output:
912985153 is a powerful number of order 9
Example
Input:
123456789
Output:
123456789 is not a powerful number
Resources
Machtige getallen zijn natuurlijke getallen die gelijk zijn aan de som van de $n$-de machten van hun cijfers voor een zekere $n \in \mathbb{N}$. Het kleinste getal $n$ waarvoor deze eigenschap geldt noemen we de orde van het machtig getal.
Neem bijvoorbeeld 912985153. Dit is een machtig getal van orde 9 omdat geldt dat $$9^9 + 1^9 + 2^9 + 9^9 + 8^9 + 5^9 + 1^9 + 5^9 + 3^9 = 912985153$$
Invoer
Een natuurlijk getal.
Uitvoer
Een regel die aangeeft of het gegeven getal al dan niet een machtig getal is. Voor machtige getallen geeft de uitvoer ook aan wat de orde van het machtig getal is. Het formaat van de uitvoer kan je afleiden uit onderstaande voorbeelden.
Voorbeeld
Invoer:
912985153
Uitvoer:
912985153 is een machtig getal van orde 9
Voorbeeld
Invoer:
123456789
Uitvoer:
123456789 is geen machtig getal
Bronnen
| Added by: | Peter Dawyndt |
| Date: | 2011-08-06 |
| Time limit: | 10s-30s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


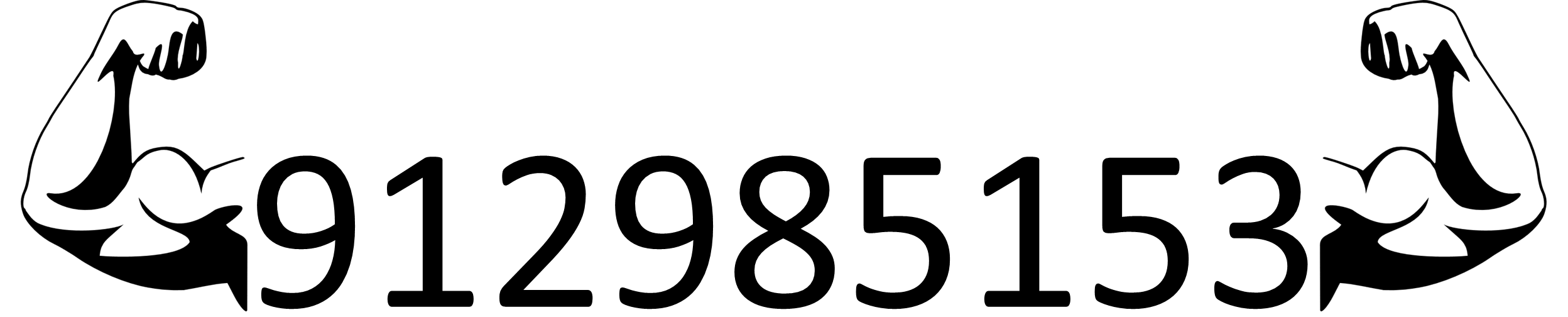

 RSS
RSS