| Submit | All submissions | Best solutions | Back to list |
PHDISP - The Philosophical Dispute |
One day, mathematician and philosopher were engaged in a heated dispute.
Philosopher said:
- Ideal line has only length and no width, therefore, no line can have an area.
Mathematician replied:
- That's as it may be, but still you can fill a square with a line in such a way that there will be no gaps.
And you can't deny that a square has an area, and he grinned.
But Philosopher still wasn't convinced:
- Show me this line, then.
- With pleasure... - responded Mathematician and scribbled some equations on a piece of paper:
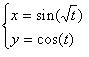
- With t increasing, the point (x, y) will move around the square, forming a line.
- So what? - asked Philosopher. How is it going to ll the entire square?
- Indeed, it will, - said Mathematician, - Whichever point inside the square you draw, the line will eventually cross that point.
- No, - replied Philosopher indignantly, - Anyway, I don't believe. When will the line cross this point? - and he put a thick dot inside the square.
Give Philosopher an answer.
Input
t – number of tests [t <= 150], than t test cases follows.
The first line of each test case contains the coordinates (x0, y0) of the dot center (-1 <= x0, y0 <= 1). The second line contains eps <= 0.0001 - the radius of the dot (the dot is essentially a small circle).
Output
For each test case output any value of t in the segment [0, 10^12], which corresponds to the line crossing the dot, or "FAIL", if the line doesn't cross the dot.
Example
Sample input: 1 0.744 0.554 0.01 Sample output: 5.3
| Added by: | Roman Sol |
| Date: | 2005-04-25 |
| Time limit: | 3s |
| Source limit: | 20000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | IX Ural Championship (Round II) |
hide comments
|
2009-10-18 15:18:28 abhijith reddy d
"Mathematician replied: - That's as it may be, but still you can ll a square with a line in such a way " "ll -> fill" |


 RSS
RSS