| Submit | All submissions | Best solutions | Back to list |
PCV2 - Problems Collection (Volume 2) |
Problem 1 How many consecutive positive integers can you find, such that the sum of digits (in decimal representation) of each of them is not divisible by 13?
Note: Because 49 is the first number for which the sum of digits divisible by 13, so for instance integers from 1 to 48 satisfy the condition.
Problem 2 You can find the solution in this file: answer.zip
Problem 3 Find the answer in this picture:
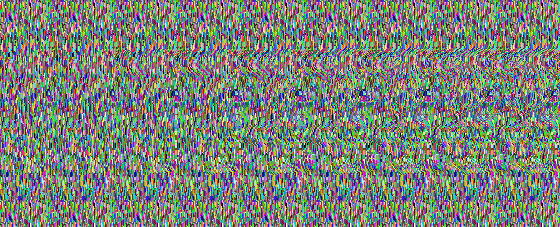
Problem 4 When looking at a number from left-to-right, if no digit is smaller than the digit to its left, then the number is called increasing; for example, 125589.
Similarly if no digit is smaller than the digit to its right, the number is called decreasing; for example, 995421.
We shall call a positive integer that is neither increasing nor decreasing a "bouncy" number; for example, 64783.
Clearly there cannot be any bouncy numbers below one-hundred, but just over half of the numbers below one-thousand (525) are bouncy. In fact, the smallest number for which the proportion of bouncy numbers first exceeds 50% is 538. Bouncy number become more and more common and by the time we reach 21780 the proportion of bouncy numbers is equal to 90%.
Find the least number for which the proportion of bouncy numbers is exactly 99%.
Problem 5 The radical of n, rad(n) - is the product of distinct prime factors of n.
For example, 1008 = 2^4*3^2*7 , so rad(1008) = 2*3*7 = 42.
If we calculate rad(n) for 1 <= n <= 10, then sort them with respect to rad(n), breaking ties by sorting with respect to the value of n, we get:
Unsorted:
n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
rad(n) = 1, 2, 3, 2, 5, 6, 7, 2, 3, 10
Sorted:
n = 1, 2, 4, 8, 3, 9, 5, 6, 7, 10
rad(n) = 1, 2, 2, 2, 3, 3, 5, 6, 7, 10
k = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Let E(k) be the kth element in the sorted n column; for example, E(4) = 8 and E(6) = 9.
If rad(n) is sorted for 1 <= n <= 100000, find E(10000).
Problem 6
Consider the infinite polynomial series: AF(x) = x*F(1) + x^2*F(2) + x^3*F(3) + ...,
where F(k) is the kth term in the Fibonacci sequence: 1, 1, 2, 3, 5, 8, ...,
that is, F(1) = 1; F(2) = 1; F(k) = F(k-1) + F(k-2).
For this problem we shall be interested in values of x for which AF(x) is a positive integer.
Surprisingly AF(1/2) = 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ... = 2
The corresponding values of x for the first five natural numbers are shown below:
1) x = sqrt(2)-1 AF(x) = 1
2) x = 1/2 AF(x) = 2
3) x = (sqrt(13)-2)/3 AF(x) = 3
4) x = (sqrt(89)-5)/8 AF(x) = 4
5) x = (sqrt(34)-3)/5 AF(x) = 5
We shall call AF(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690.
Find the 15th golden nugget.
Problem 7
Euler's totient function F(n) is defined as the number of positive integers not exceeding n that are relatively prime to n, where 1 is counted as being relatively prime to all numbers. So, for example, F(20) = 8,
because the eight integers 1, 3, 7, 9, 11, 13, 17, and 19 are relatively prime to 20. The table below shows values of F(n) for the first 10 integers:
F(1) = 1, F(2) = 1, F(3) = 2, F(4) = 2, F(5) = 4,
F(6) = 2, F(7) = 6, F(8) = 4, F(9) = 6, F(10) = 4
Euler's totient valence function v(n) is defined as the number of positive integers k such that F(k) = n. For instance, v(8) = 5 because only the five integers k = 15, 16, 20, 24, and 30 are such that F(k) = 8. The table below shows values of v(n) for n <= 16. (For n not in the table, v(n) = 0).
| n | v(n) | k such that F(k)=n |
| 1 | 2 | 1, 2 |
| 2 | 3 | 3, 4, 6 |
| 4 | 4 | 5, 8, 10, 12 |
| 6 | 4 | 7, 9, 14, 18 |
| 8 | 5 | 15, 16, 20, 24, 30 |
| 10 | 2 | 11, 22 |
| 12 | 6 | 13, 21, 26, 28, 36, 42 |
| 16 | 6 | 17, 32, 34, 40, 48, 60 |
Evaluate v(2^1000).
Problem 8 In how many ways can 50! be expressed as a sum of two or more consecutive positive integers?
Problem 9 Imagine you have a crystal in the shape of an equilateral triangle, one unit long on each side. In the right conditions, the crystal starts to grow. After one minute, two sides grow from each side of the triangle that are perfectly symmetrical. The result is a six-pointed star, that has sides that are exactly 1/3 of the length of the side they grew from. After another minute, each side sprouts two more sides that are exactly 1/3 of the length of the side they came from. See the pictures to get a better idea:
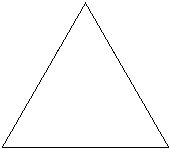
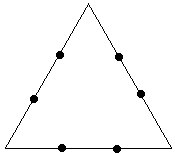
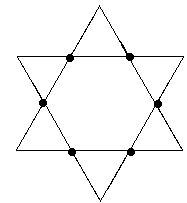

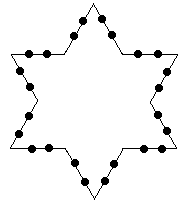
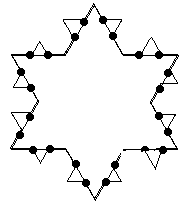
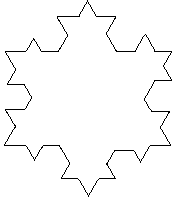
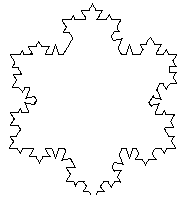
Your challenge is to find the perimeter (rounded to the nearest whole number) after one hour, thirty-three minutes.
Problem 10
One more picture:
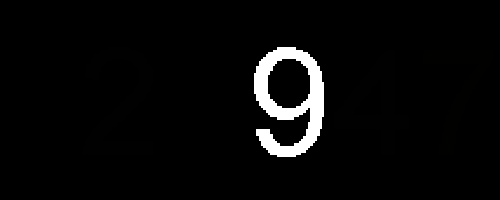
Input
There is no input for this problem.
Output
Output the answer as a set of lines. In each line first give the number of the problem and then the answer to this problem. If any of the answers are incorrect, you will receive Wrong Answer.
Score
For each solved problem you'll recieve exactly one point (10 points maximum, if all problems are solved correctly).
Example
Output:
1 6174046 2 AnsweR 5 806257 8 51146700
It's just the example of what the output should look like. If all 4 answers are correct (problems 1, 2, 5 and 8), you will recieve 4 points.
| Added by: | Roman Sol |
| Date: | 2006-04-11 |
| Time limit: | 0.100s |
| Source limit: | 10000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | TEXT |
| Resource: | ZCon 2007 |


 RSS
RSS