| Submit | All submissions | Best solutions | Back to list |
JUMPDORA - JUMPING DORA |
Jumping Dora wants to reach her destination from the source as soon as possible. Dora's initial position is (0, 0) and the destination is (m - 1, n - 1)
If Dora is currently at (i, j), she can either move to (i, j + 1) or (i, j + 1 + C[i][j]) or (i + 1, j) or (i + 1 + C[i][j], j). Dora cannot move to the blocked positions.
Note that you can jump when there are blocks in between.
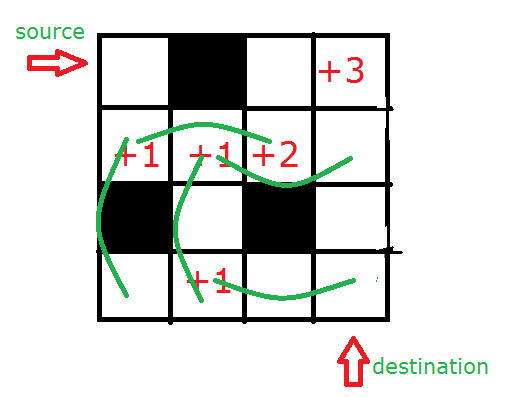
Find the shortest time required to reach the destination.
Input
The first line consists of an integer t, the number of test cases. For each test case, the first line consists of two integers m and n representing the number of rows and columns. Then follows the description of the matrix C.
Output
For each test case find the shortest time required to reach the destination. If it is impossible, print -1.
Constraints
1 <= t <= 100
2 <= m, n <= 100
C[i][j] = { [0 - 9], # }
Note: There may be no path to the destination from the source.
C[0][0] and C[m - 1][n - 1] are always 0.
Example
Input: 1 4 4 0#03 1120 #0#0 0100 Output: 4
| Added by: | cegprakash |
| Date: | 2012-10-17 |
| Time limit: | 1s-10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 GOSU |
hide comments
|
2022-05-24 02:26:59
ok |
|
|
2015-05-18 12:19:44 Shubham
finally AC easy questn reccursn gets TLE use DP.....nd my personl advice use INT_MAX in c++ carefully....i got many WA becoz of that....-__-..:/ |
|
|
2014-04-17 09:53:33 cegprakash
:D okay |
|
|
2014-04-17 09:53:33 :D
Sorry, but I feel it's too basic for classical. Adding variables to moves makes for a minor variety in the basic maze problem and it's almost the same difficulty as if C[i][j]==0 for all fields. |


 RSS
RSS